中国船舶重工集团有限公司第七一〇研究所,湖北 宜昌 443003
摘 要 MEMS陀螺仪作为低成本惯性测量单元在载体姿态监测与导航控制中有着广泛应用。根据三轴光纤陀螺仪标定的数学模型,设计了三轴MEMS陀螺仪标定的数学模型及标定实验;介绍了数学模型中陀螺仪标度因数、安装误差系数以及固定常值漂移的计算与处理方法。理论分析与实验结果表明:该标定方法原理简单、易于实现,且标定结果精度高,标定后的解算矩阵可为后续姿态解算和导航控制提供较为准确的量测数据。
关键词 三轴MEMS陀螺仪;安装误差标定;误差补偿
0 引言
传统磁罗盘主要由三轴加速度计和三轴磁力计构成(也称为六轴磁罗盘),三轴加速度计主要用于测量地球重力加速度,根据所测得的数据,求解载体的俯仰角和横滚角,利用求出的俯仰角和横滚角,同时结合三轴磁力计测得的地磁场数据,求解出载体的磁方位角[1]。
当载体处于准静态(静止或匀速运动)时,三轴加速度计可准确测量地球重力加速度,从而准确求解出载体姿态角。当载体处于动态时,三轴加速度计除了测量地球重力加速度外,还会测得载体自身所产生的加速度,导致姿态角计算不准。因此,六轴磁罗盘只能准确测量准静态下载体的姿态角,而无法用于动态条件时载体姿态角的准确测量。但在实际应用中,大多数载体都是处于动态,由于载体运动对陀螺仪的影响较小,利用这一特性可以解决动态条件下载体姿态角精确测量问题[2]。
近年来,随着MEMS陀螺仪技术的发展,MEMS陀螺仪技术水平已取得了长足的进步,将三轴MEMS陀螺仪集成到传统磁罗盘中构成九轴磁罗盘(AHRS)已成为现实[3]。然而,三轴MEMS陀螺仪由于存在固定常值漂移、安装误差、标度因数误差等会直接影响九轴磁罗盘姿态计算[4],因此在使用三轴MEMS陀螺仪之前对其进行精确的标定过程是非常必要的。
1 陀螺仪标定原理
MEMS陀螺仪对姿态误差产生直接影响,其主要表现是MEMS陀螺仪固定常值漂移、陀螺仪的安装误差对捷联惯导系统的姿态误差的影响[5]。由于MEMS陀螺仪的精度相对较差,因此可以忽略二次交叉项后得到MEMS陀螺仪输出数学模型[6~7]:
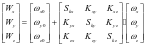 (1)
(1)
式中,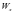 、
、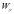 、
、 为MEMS陀螺仪的输出值;
为MEMS陀螺仪的输出值;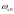 、
、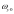 、
、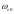 为MEMS陀螺仪的零偏;
为MEMS陀螺仪的零偏;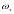 、
、 、
、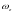 为MEMS陀螺仪的输入值;
为MEMS陀螺仪的输入值;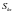 、
、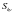 、
、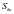 为MEMS陀螺仪的标度因数;
为MEMS陀螺仪的标度因数; 、
、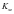 、
、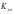 、
、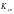 、
、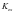 、
、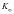 为MEMS陀螺仪的安装误差系数。
为MEMS陀螺仪的安装误差系数。
将MEMS陀螺仪通过夹具固定安装在速率转台上,并使MEMS陀螺仪的敏感轴x轴、y轴、z轴分别对应转台的3个转动轴,即内框转动轴、中框转动轴、外框转动轴,实验测试时标定轴与转台对应的转轴平行。给转台一个固定的速率值,测量MEMS陀螺仪的输出值。
由式(1)可得MEMS陀螺仪的刻度因数和漂移采用最小二乘法的求解方法计算分别为:
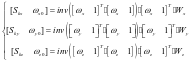 (2)
(2)
采用最小二乘法的求解方法计算MEMS陀螺仪的安装误差系数为:
 (3)
(3)
求得MEMS陀螺仪的误差参数后,可通过陀螺仪的原始输出求得MEMS陀螺仪的真实输入值:
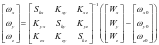 (4)
(4)
2 MEMS三轴陀螺仪标定试验
实验借助三轴位置速率电动转台,转台速率精度优于0.01°/s,将九轴磁罗盘固定安装在三轴速率转台上,并使MEMS陀螺仪的敏感轴x轴、y轴、z轴分别对应转台的3个转动轴,即内框转动轴、中框转动轴、外框转动轴,实验测试时标定轴与转台对应的转轴平行。它可以为九轴磁罗盘提供输入角速度,。在试验中控制三轴转台的外框、中框、内框速率分别取±10°/s,±63°/s,±160°/s,±275°/s的速率依次转动,待转台转速稳定后采集稳定转速下30s的数据。
2.1 MEMS陀螺仪的速率标定方法
陀螺仪先通电静止预热10分钟,采集记录陀螺仪静止时的输出值。然后启动转台进行动态速率测试。以三轴转台外框转动速率为例,介绍陀螺仪敏感轴z轴的动态特性测试。用软件控制三轴转台的外框速率分别取±10°/s,±63°/s,±160°/s,±275°/s的速率依次转动,待转台转速稳定后采集稳定转速下30s的数据,忽略转台的起始和停止阶段,求得在某输入角速率下MEMS陀螺仪输出的平均值作为该输入角速率值下的MEMS陀螺仪输出值,将实验数据填入对应表格。
2.2 实验数据处理
将转台在各个速率下转速稳定后采集得到的数据取均值作为该速率下三轴MEMS陀螺仪的输出值,将得到的输出值记录到表1~表3中。
表1 标定X轴时MEMS陀螺仪3个敏感轴的输出(°/s)
| 转台给出值 | 275 | 160 | 63 | 10 | -10 | -63 | -160 | -275 | ||||||||
| 陀螺仪实际输出值 | X轴 | 272.810 | 157.901 | 60.971 | 8.019 | -11.968 | -64.932 | -161.876 | -276.798 | |||||||
| Y轴 | -8.461 | -5.464 | -2.956 | -1.576 | -1.062 | 0.316 | 2.818 | 5.799 | ||||||||
| Z轴 | -8.664 | -5.798 | -3.385 | -2.067 | -1.570 | -0.242 | 2.170 | 5.039 | ||||||||
表2 标定Y轴时MEMS陀螺仪3个敏感轴的输出(°/s)
| 转台给出值 | 275 | 160 | 63 | 10 | -10 | -63 | -160 | -275 | |
| 陀螺仪实际输出值 | X轴 | -5.000 | -3.742 | -2.683 | -2.093 | -1.871 | -1.301 | -0.235 | 1.025 |
| Y轴 | 274.564 | 159.206 | 61.893 | 8.728 | -11.339 | -64.514 | -161.830 | -277.219 | |
| Z轴 | -3.691 | -2.909 | -2.252 | -1.905 | -1.769 | -1.398 | -0.738 | 0.038 | |
表3 标定Z轴时MEMS陀螺仪3个敏感轴的输出(°/s)
| 转台给出值 | 275 | 160 | 63 | 10 | -10 | -63 | -160 | -275 | |
| 陀螺仪实际输出值 | X轴 | -4.490 | -3.443 | -2.561 | -2.075 | -1.900 | -1.417 | -0.529 | 0.518 |
| Y轴 | -2.925 | -2.246 | -1.673 | -1.357 | -1.238 | -0.936 | -0.362 | 0.322 | |
| Z轴 | 275.628 | 159.583 | 61.727 | 8.259 | -11.926 | -65.411 | -163.280 | -279.319 | |
利用公式(2)和(3)计算出陀螺仪的刻度因子、零偏、非正交度参数,得到该陀螺仪的原始输出求得MEMS陀螺仪的真实输入值之间的关系:
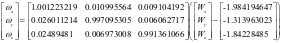 (5)
(5)
取陀螺仪静态测试数据的三轴输出求平均值作为零偏,得到的结果如表4所示。
表4 MEMS三轴数字陀螺仪的静态测试
| X轴零偏(°/s) | Y轴零偏(°/s) | Z轴零偏(°/s) |
| -1.99208 | -1.29988 | -1.84303 |
陀螺仪静态测试得到的零偏值与动态最小二乘法计算得到的零偏值一致,说明计算得到的零偏与静止时刻的零偏一致,验证了校准算法的有效性。
3 标定结果验证
为了验证该标定方法标定出的数学模型的正确性和有效性,做完标定试验后另外测试X轴另外的一系列速率点,方法与测试标定试验的方法一致,将数据带入公式(5)得到解算陀螺仪真实角速率与误差如表5所示。
表5 MEMS三轴数字陀螺仪的X轴标定结果验证
| 理论值(°/s) | 实测值X(°/s) | 校正后X(°/s) | 实测误差/% | 校正后误差/% |
| 100 | 97.95156 | 100.00697 | -2.04844 | 0.00697 |
| 40 | 37.98974 | 40.00258 | -5.02564 | 0.00644 |
| 16 | 14.01490 | 16.01063 | -12.40685 | 0.06646 |
| 2.5 | 0.50894 | 2.49515 | -79.64239 | -0.19400 |
| -2.5 | -4.49076 | -2.50807 | 79.63046 | 0.32270 |
| -16 | -17.96703 | -15.99405 | 12.29395 | -0.03720 |
| -40 | -41.94752 | -39.99158 | 4.86879 | -0.02106 |
| -100 | -101.91053 | -99.99734 | 1.91053 | -0.00266 |
可以看出,陀螺仪的输出误差从标定前最大接近2°/s降低到标定全量程范围内后的<±0.01°/s,误差降低了1~2个数量级。以X轴传感器角速率100°/s为例得到三轴陀螺仪标定前后的输出结果对比如图1所示。
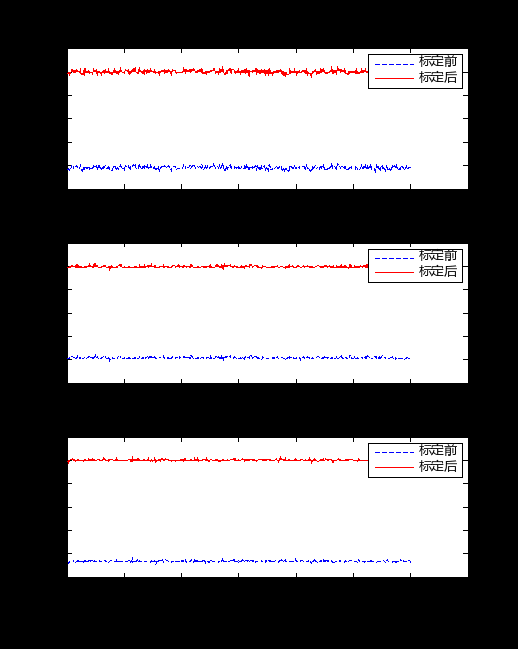
图1 X轴陀螺仪补偿前后输出曲线
陀螺仪标定补偿结果以MIMU中X轴向陀螺仪为例,对陀螺仪理论输出角速度值为97.9516°/s的数据点进行分析,补偿前X轴上测试得到的角速度值大小为100°/s,补偿后变化为100.0070°/s;同时,补偿前X轴向上角速度投影到Y、Z轴上的角速度分量分别为-3.9161°/s、-4.3047°/s,补偿后减小为-0.0101°/s、0.0286°/s,分析可知补偿后的陀螺仪输出结果精度比补偿前提高了1~2个数量级。
4 结论
本文参考光纤陀螺仪的标定方法,建立MEMS三轴陀螺仪的误差数学模型,设计MEMS陀螺仪的速率标定方法,该方法能够标定出九轴磁罗盘中三轴MEMS陀螺仪零漂、静态刻度因子和安装误差。从工程应用角度考虑,只要准确建立MEMS陀螺仪的数学模型就可进行速率标定,这种方法原理简单,易于实现,且精度较高。但这种标定方法只对MEMS陀螺仪的常值漂移进行了补偿,没有考虑到MEMS陀螺仪的随机漂移,也没有考虑温度对传感器的影响。因此,如果要继续提高系统的精度,还需在MEMS陀螺仪的噪声处理及温度补偿上做进一步的工作。
参考文献
[1] 谭志斌,赵祚喜,张霖,等.MEMS惯性传感器的三轴转台实验研究 [J].电子测量技术,2012,35(4):110-115.
[2] 宋丽君.基于MEMS器件的航向姿态测量系统的研究[D].西安:西北工业大学,2007.
[3] 陈瑜,张铁民.低成本三轴微数字陀螺仪标定方法及实验研究 [J].仪表技术与传感器,2014,48(4):48-51.
[4] 冀海燕.高精度惯性陀螺仪误差系数的快速自标定方法研究 [J].工程与试验,2009,49(4):28-30.
[5] 宋丽君,秦永元.MEMS陀螺仪的一种实用标定法[J].压电与声光,2010,32(3):372-374,378.
[6] 袁建国,袁艳涛,刘飞龙.MEMS陀螺仪的一种新颖高精度标定算法研究 [J].重庆邮电大学学报,2014,26(5):666-669.
[7] 陈瑞娟.吴春梅.小型化MEMS制导仪标定与误差补偿方法研究 [J].导航定位与授时,2015,2(6):75-80.
(注意:1、图要清楚,图中文字要用5、6号宋体,要能够看得清楚。2、注意公式和单位的正斜体,变量要用斜体。)