预制带肋底板混凝土叠合试件动力学显式方法初探

预制带肋底板混凝土叠合试件动力学显式方法初探

刘振 黄仕利 苏成生

马鞍山华亿工程技术有限公司

摘 要：近年来，我国房地产业高速发展，对混凝土等建筑材料需求量、建设效率和建筑绿色环保的要求越来愈高。预制带肋底板混凝土叠合板可以实现提高建设效率还能实现建筑材料的绿色环保。本文对叠合界面有限元仿真分析的显式分析方法进行了研究，得出了叠合面材料稳定极限的计算方法。

关键词：预制带肋底板混凝土；叠合；动力学；建模

引言

预制带肋底板混凝土叠合板在合理的处理了先、后浇混凝土叠合面力学属性、预设孔洞内混凝土剪力键、横向穿孔钢筋与混凝土的粘结滑移等问题的基础上，利用ABAQUS有限元软件提出了适用于预制带肋底板混凝土叠合试件进行叠合面仿真分析的建模方法，可以得出了组成叠合面抗剪承载力的各项分力所占比例，让其具有更好的建筑使用性能^[1-3]。

1叠合界面有限元仿真分析的方法研究

叠合面是新老混凝土的交界面，从微观结构上对该界面进行研究可知：可将界面分为扩散层、强效应层和弱效应层三个层区，从老混凝土界面开始深入新混凝土100-200μm的过渡层是粘结界面的最薄弱层，其界面的粘结作用力主要为各种水化产物间的机械咬合力。将如此薄弱窄小的一个界面层直接建立有限元模型进行分析，对于从宏观力学的角度去探究叠合面受力性能的研究人员而言是很不方便的，故一般研人员进行叠合结构的有限元受力分析时，都对叠合面进行了一定的简化处理^[4]。

最简单的处理方式是不考虑叠合面的粘结滑移，将叠合结构整体建模，只考虑新老混凝土强度的差异。此方法固然简单但过于粗糙，对于试件内部剪应力较小的受弯叠合试件尚可作此理想假定，但对于承受较大剪力作用的叠合试件，叠合面的粘结-滑移性能将对试件的承载力将产生较为明显的影响，此时忽略叠合面的粘结滑移属性是不合理的。

第二种处理方式是采用三维弹簧单元(Spring2)来进行叠合面受力行为模拟。Spring2是用来连接2个节点的弹簧单元，可以通过定义弹簧的刚度，应力-变形曲线，即力和相对滑移曲线的函数来定义弹簧的非线性性能^[5-6]。通常认为，在三维有限元分析中，新、老混凝土的相互作用是三维的，可以通过法向（垂直于新老混凝土粘结面)、纵向切向(平行于粘结面且沿着加载方向）和横向切向(平行于粘结面且垂直于加载方向)这3个方向的弹簧单元来进行模拟。并通过引入这3个方向的劲度系数来分别定性描述新老混凝土的相互作用。该方法可以通过前期的试验工作确定弹簧的力-位移关系，进而较为准确的模拟叠合面在粘结破坏前的力学性能，但无法定义弹簧的破坏准则，故难以模拟叠合面粘结破坏后的力学特征，且该方法需对叠合面上新、老混凝土的对应节点均使用弹簧连接上，对于模型较大的叠合结构而言，建模工作未免过于繁重。

第三种处理方式是建立专门的叠合层混凝土单元，如cohesiveelement(ABAQUS)或contactelement(ANSYS、MAC)。基于界面相对位移和应力之间关系建立的界面单元能够有效地模拟混凝土叠合界面的力学行为，甚至可以将界面单元视为零厚度界面单元，相应的界面单元的材料模型采用牵引力-相对位移(traction-separate模型)进行描述。这种单元的建立方法有两种：第一种方式是先将结构整体建模，再在接触面部位划分出一薄层作为叠合面混凝土单元，这种方式建立的叠合层混凝土单元与其他单元共用节点，并通过共用节点传递力和位移，但划分网格时较为复杂，网格没有划分好的话容易造成计算结果无法收敛。第二种建立方法为独立建立一个薄层作为一个部件，将该薄层独立赋予材料属性后直接采用“tie”命令与其他部件粘结起来。该方法可以单独划分薄层网格，且网格密度不必与其他部件的网格密度一致，较为方便^[7]。采用建立专门的叠合层混凝土单元的处理方式可以较为直观的观察叠合面的损伤破坏形态，且模拟叠合面粘结-滑移的效果较好，但模型的将各部件粘结在一起时较为麻烦，前处理工作较为复杂繁琐，适合用于简单模型的精确分析。

第二种处理方式是将先、后浇混凝土的叠合面抗剪性能问题看作两个不同部件之间的接触问题。接触问题是工程实际中常见的典型非线性问题，大多数接触问题都难以用解析法求解。有限元方法出现后，研究人员普遍采用数值方法对接触问题进行求解，取得了很好的效果。从1881年Hertz导出并求解了接触问题的积分方程开始至今，接触问题得到了极大的发展，多种大型通用有限元商业软件，如ANSYS、ABAQUS、MSC.Marc等都包含有专门分析接触问题的接触模块，此不赘述。利用“接触模块”的建模方式，研究人员可以指定接触面并通过赋予接触面属性的方式定义叠合面的力学行为。由于不用考虑新、老混凝土的网格密度差异和节点的坐标对应问题，建模工作的效率和精确性得到了很大的提升。这种预制带肋底板混凝土叠合空心楼板的试验与数值模拟研究叠合面处理方式的关键在于接触面接触属性(surface-basedcohesivebehavior)的定义。其主要工作是定义接触面的切向及法向力学模型，对应模拟叠合面的切向及法向力学行为。本文认为这种建模方式有一个值得注意之处在于，摩擦力相对于叠合面的粘聚力是独立的。即surface-basedcohesivebehavior型内聚力接触和摩擦接触同时设置时，在surface-basedcohesivebehavior未破坏之前，摩擦力都是处于一种休眠状态，当surface-basedcohesivebehavior发生破坏了，才会触动摩擦力起作用。显然surface-basedcohesivebehavior并不适用于摩擦力与粘聚力同时产生且同时发展的受力模式的数值模拟。因此，采用surface-basedcohesivebehavim型内聚力接触的方式模拟界面行为应考虑是否与实际受力情况相符。

本文考虑到模型的实际情况，将叠合面的力学行为视为新、老混凝土的接触问题，利用ABAQUS中的接触模块定义叠合面的接触力学模型，对push-off推开试验进行受力全过程的有限元模拟分析。

2动力学显式有限元方法介绍

采用大型通用有限元分析软件ABAQUS建立有限元模型，对预制带肋底板混凝土叠合试件的叠合面水平抗剪力学行为进行分析。ABAQUS有两个主要的分析模块：ABAQUS/Standard和ABAQUS/Explicit。ABAQUS/Standard采用隐式算法，通过进行迭代求解确定问题的解答，能够求解广泛领域的线性和非线性问题，包括静力、动力、构件的热和电响应等问题，但每次迭代都需要求解大量的线性方程组，计算代价昂贵。且在隐式分析中，高度非线性的接触行为或者材料的退化和失效常常导致严重的收敛困难而导致计算失败。ABAQUS/Explicit采用显式动力学有限元格式，通过前一增量步显式地推动力学状态，确定解答无需进行迭代，不存在收敛问题，不需要定义收敛准则，适用于模拟如爆炸冲击这种短暂、瞬时的动力问题，也比较适用于处理高度非线性的接触问题(如成型问题)^[8]。

预制带肋底板混凝土叠合试件的叠合面水平抗剪行为的模拟，包含了材料的失效及叠合面的粘聚、摩擦、滑移等问题，非线性行为较强，采用ABAQUS/Standard模块进行分析会存在收敛问题，因而本文利用ABAQUS/Explicit模块对试件的力学性能进行有限元分析。由于本次加载属于静力加载，在ABAQUS/Explicit模块中可以采取准静态加载的方式进行模拟。在求解准静态问题上，显式求解方法己经证明是有价值的。另外ABAQUS/Explicit在求解某些类型的静态问题方面比ABAQUS/Standard更容易。尤其在在求解复杂的接触问题时，由于不存在收敛问题，显式过程相对于隐式过程具备更大的优势。此外，当模型很大时，显式过程比隐式过程需要较少的系统资源。

ABAQUS/Explicit应用中心差分法对方程进行显式的时间积分，应用一个增量步的动力学条件计算下一个增量步的动力学条件。

在增量步开始时，程序求解如下动力学平衡方程：

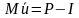（1.1）

式中：M为节点质量矩阵，ü为节点速度，P为施加的外力，I为单元内力。

计算当前增量步开始时(t时刻)的加速度为：

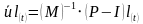（1.2）

在显式算法中，质量矩阵总是采用对角矩阵或者集中质量矩阵，所以在求解式（1.1）中加速度时变得简单，不需求解联立方程。

采用中心差分方法对加速度在时间上进行积分，在计算速度的变化时假定加速度为常数。当前增量步中点的速度即等于前一个增量时间的中点速度加上时间增量段内速度的变化值：

（1.3）

增量步结束时的位移即等于当前速度对时间的积分加上增量步开始时的位移值：

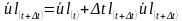（1.4）

上述过程即“显式”算法的核心步骤，即根据动力学平衡条件计算出加速度，假定在增量步时间内加速度为常数，计算出该增量步中点的速度和增量步结束时的位移值，在时间上“显式地”前推速度和位移。使用该方法时，要产生精确的结果，增量步内加速度需保持几乎为常数，所以要求时间增量步长必须相当小，这意味着一个分析需要成千上万个增量步，但由于分析过程中不需要联立求解方程组，因而每一个增量步的计算成本很低。在显式分析中，单元计算消耗了大部分的计算成本，其计算包括单元应变计算，并通过材料本构关系计算单元应力，进而确定内力。

以下总结了显式动力学方法：

1)节点计算

(1)动力学平衡方程

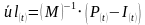
(2)对时间显式积分

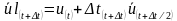
2)单元计算

（1）根据应变速度ε计算单元应变增量d

（2）根据本构关系计算应力

(1.5)

（3）集成节点内力

3)设置时间t为t+△t，返回到步骤1。

在前面己经提到，使用显式分析方法时要产生精确的结果，要求时间增量步长必须相当小。显式分析是有条件稳定的，要求时间步长不超过稳定限制，即临界稳定时间步长。如果增量超过临界稳定时间步长，可能导致数值不稳定，解答不收敛，此时整体的能量将不再平衡。

ABAQUS/Explicit对临界稳定日寸间步长的确定有两种方法确定，即基于整体的估计和基于单元的估计。采用自动时间步长控制时，默认情况是ABAQUS在分析初始阶段采用基于单元的估计方法计算临界稳定时间，在分析过程中采用基于整体的方法估计临界稳定时间。

以在系统中的最高频率(ω_max)的形式定义稳定性限制，这是基于整体的估计方法。无阻尼的稳定极限由下式定义：

(1.6)

而有阻尼的稳定极限由下面的表达式定义：

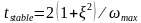△(1.7)

式中，ξ为ω_max振型对应的阻尼比。

基于单元估计的临界稳定时间步长定义为：

(1.8)

式中：L^e为单元长度，C_d为材料波速。步长作为近似值，可以采用最短的单元尺寸。单元长度越短，稳定极限越小。波速是材料的一个特性。对于泊松比为零的线弹性材料，

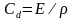(1.9)

其中，E是弹性模量;ρ是材料密度。从式(1.8-1.9)可知，材料的刚度越大，波速越高，导致临界稳定时间步长越小；密度越高，波速越低，导致临界稳定时间步长越大。

3.结论

基于单元的最小时间步长(稳定极限)估计可以直观的理解为是当膨胀波通过由单元特征长度定义的距离时所需要的时间。如果知道最小的单元尺寸和材料的波速，就能够估算稳定极限。例如，如果最小单元尺寸是5mm，膨胀波速是5000m/s，那么稳定的时间增量就在lx10^-6s的量级上。从式(1.8)和式(1.9)可见，不同的材料的波速不一样，所以不同的材料稳定极限也不同。从式(1.8)还可知，不同的单元尺寸对稳定极限也有影响。

参考文献：

[1] 贺灵童，陈艳.建筑工业化的现在与未来[J].工程质量，2013，（2）：1-8.

[2] Cook J P.Composite Structure methods[M].New York：mc Graw-Hill Book Company inc，1976.

[3] Ziad Bayasi，Henning Kaiser， Miguel Gonzales. Composite Slabs with Corrugated Simcon Deck as Alternative for Corrugated Metal Sheets[J].Journal of Structural Engineering，2001，127（10）：1198-1205.

[4] 全国钢筋混凝土结构标准技术委员会.原西德混凝土和钢筋混凝土结构设计和施工规范[S].北京：中国建筑工业出版社，1972，345-450.

[5] 岳建伟.槽形芯板预应力叠合板试验与应用研究[D].天津:天津大学，2003.

[6] 曾垂军，吴方伯，刘锡军等.新型叠合结构体系的设计与施工[J].建筑科学，2006，22（4）：67-71.

[7] 吴方伯，黄海林，陈伟等.预制带肋薄板混凝土叠合板件受力性能试验研究[J].土木建筑与环境工程，2011，33（04）：7-12+19.

[8] 罗荣.PKG预制底板及其叠合板的设计原理与受力性能研究[D].昆明理工大学，2018.

2