中国水利水电第七工程局有限公司 四川省 成都市 610000
摘 要：本文以杨房沟水电站拱坝混凝土模板施工测量放样为例，详细介绍了利用可编程便携计算器CASIO fx-5800P编写测量放样程序的设计思路及现场应用，体现了利用程序设计配合测量放样工作在缩短现场测量数据计算时间、提高测量工作效率、促进工程进度方面的重要作用。
关键词：杨房沟水电站；双曲拱坝；测量放样；CASIO fx-5800P；程序设计
杨房沟水电站位于四川省凉山彝族自治州木里县境内的雅砻江中游河段上，上距孟底沟水电站37km，下距卡拉水电站33km，电站坝址距下游杨房沟沟口约450m。电站开发任务为发电，总装机容量1500MW，安装4台375MW的混流式水轮发电机组。杨房沟水电站为一等工程，工程规模为大（1）型。
杨房沟水电站双曲拱坝体型复杂，上、下游面为曲面，其尺寸和表面曲率都处于连续的不断变化之中，上下游模板施工过程中需要不断地进行调整并快速安装拆卸，同时拱坝轮廓线的测量放样、模板校准、模板检测的偏差计算繁琐复杂，如何快速精确的完成现场施工测量偏差计算，是保证拱坝体型尺寸满足设计要求、混凝土浇筑快速高质量施工的关键因素。
以拱坝混凝土模板施工为例，其测量放样方法为：首先根据现场模板安装需要实测任意点坐标，计算点至设计曲面的径向偏距，然后按偏距差值沿径向方向移动测点，即可放样出立模点，同理可实测模板上任意点，计算出模板安装偏差，完成模板校准。
杨房沟水电站双曲拱坝体型复杂，测量放样及模板验收工作量大，计算过程相对复杂，计算中涉及参数多，随着高程的变化涉及参数也在变化。现场施工测量放样中使用目前工程测量中广泛应用的可编程便携计算器CASIO fx-5800P完成数据计算，利用编程功能编写出拱坝混凝土模板施工测量放样程序，将大量计算参数和公式写进程序内部，现场只需要将实测任意点坐标输入计算器，通过程序计算，即可显示任意想要的设计值及偏差值。使用拱坝混凝土模板施工测量放样程序进行测量放样，从输入坐标到输出结果只需要几秒钟，计算结果快速精确，满足施工精度要求。
杨房沟水电站拱坝坝型为抛物线型混凝土双曲变厚拱坝，坝顶高程2102m，最大坝高155m，拱冠梁顶厚9m，底厚32m，厚高比0.206，最大拱端厚度34.9m。坝顶中心线弧长362.17m，共分18个坝段。
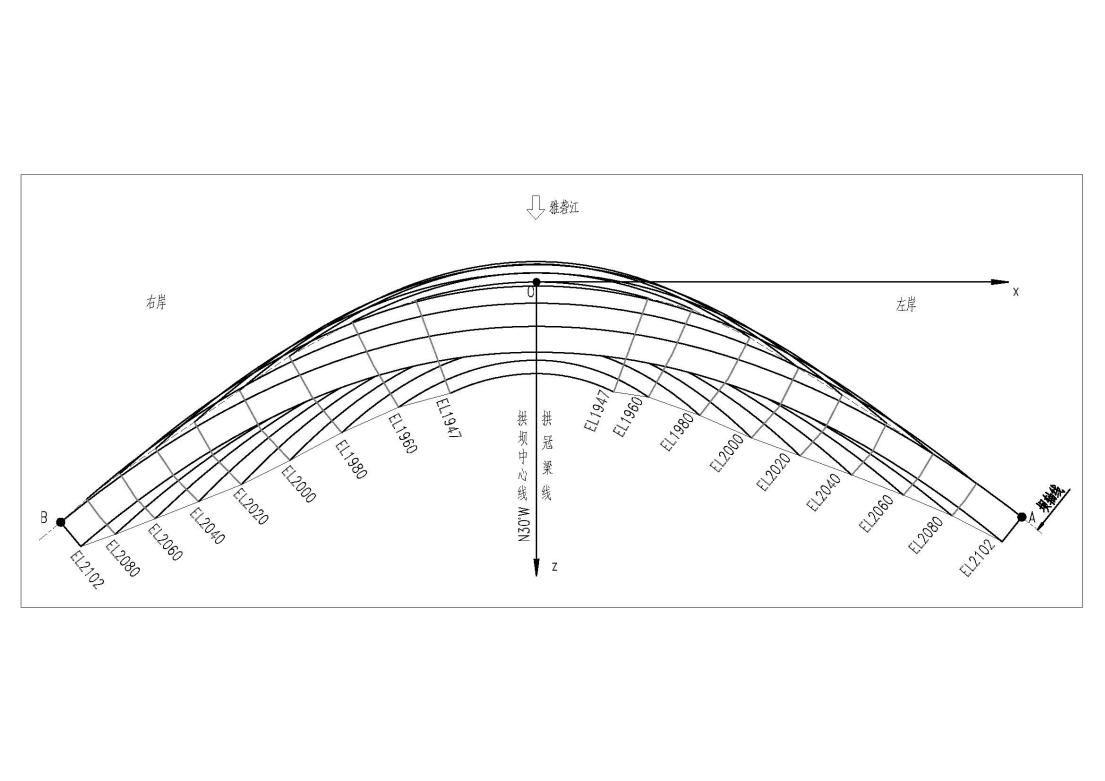
图1 拱坝三维效果图 图2 拱坝体形平面图
拱圈中心线参数方程：
左岸部分：X=Rcl·tan（Φl）
Z=Zcu+Tc/2+Rcl/2·tan2（Φl）
右岸部分：X=Rcr·tan（Φr）
Z=Zcu+Tc/2+Rcr/2·tan2（Φr）
拱圈中心线任一点拱圈中心线弧长公式：
左岸部分：Ti=Tc+（Tl-Tc）·（Si/Sa）2.2
Zcu=-0.358992×10-5Y3+0.304409×10-2Y2-0.285587Y+0.7002×10-7
Tc=-0.126543×10-5Y3-0.374475×10-4Y2-0.112181Y+0.3200×102
Tl=0.746601×10-5Y3-0.203472×10-2Y2-0.181831×10-1Y+0.3490×102
Tr=0.183804×10-5Y3-0.102940×10-2Y2-0.369251×10-1Y+0.3461×102
Rcl=-0.350602×10-4Y3+0.137792×10-1Y2-0.537332Y+0.9030×102
Rcr=-0.248893×10-4Y3+0.105619×10-1Y2-0.421068Y+0.9820×102
参数说明：Zcu：拱冠梁上游面的Z坐标（坐标正向指向下游）；Tc：拱冠梁处的拱圈厚度；Tl：左拱端拱圈厚度；Tr：右拱端拱圈厚度；Rcl：拱冠梁处左岸侧的拱圈中心线曲率半径；Rcr：拱冠梁处右岸侧的拱圈中心线曲率半径；Φl：拱端中心线左岸拱端半中心角；Φr：拱端中心线右岸拱端半中心角；Ti ，Si：拱圈中心线任一点对应的拱圈厚度及拱圈中心线弧长（从拱冠梁起算）；Sa：左或右拱端处对应的拱圈中心线弧长；Y：计算位置高程-1947.00。
拱坝体形控制参数见表1
表1 拱坝体形控制参数表
| 高程(m) | 拱厚(m) | 拱冠梁上游面Z坐标(m) | 半中心角(°) | 曲率半径(m) | |||||||
| 拱冠Tc | 左拱端Tl | 右拱端Tr | 左岸Φl | 右岸Φr | 左岸Rcl | 右岸Rcr | |||||
| 2102.00 | 9.000 | 11.000 | 11.000 | 15.500 | 38.652 | 39.957 | 207.500 | 194.000 | |||
| 2080.00 | 13.440 | 14.054 | 15.814 | 7.418 | 39.701 | 41.771 | 180.092 | 170.472 | |||
| 2060.00 | 17.020 | 17.637 | 19.945 | 1.419 | 40.814 | 43.082 | 154.940 | 149.572 | |||
| 2040.00 | 20.225 | 21.616 | 23.751 | -3.119 | 41.750 | 44.081 | 134.304 | 130.371 | |||
| 2020.00 | 23.119 | 25.634 | 27.144 | -6.022 | 42.230 | 44.613 | 110.865 | 114.064 | |||
| 2000.00 | 25.761 | 29.332 | 30.035 | -7.120 | 41.651 | 43.407 | 92.308 | 101.846 | |||
| 1980.00 | 28.212 | 32.353 | 32.337 | -6.238 | 37.778 | 39.512 | 86.314 | 94.912 | |||
| 1960.00 | 30.533 | 34.336 | 33.960 | -3.206 | 28.970 | 31.054 | 85.566 | 94.456 | |||
| 1947.00 | 32.000 | 34.900 | 34.610 | 0.000 | 20.051 | 20.179 | 90.300 | 98.200 | |||
由于该拱坝属于非对称型抛物线双曲拱坝，在同一高程面内左右拱圈任意拱端半中心角各不相等，实际放样过程中可提前由《杨房沟拱坝半中心角计算程序》计算而得。
由于拱坝上下游轮廓线方程及公式未知，无法直接求出任一点到设计轮廓线的径向偏距及对应的设计坐标。但拱圈中心线为抛物线型，且其参数方程已知，可以求得任一点到拱圈中心线的距离，再根据拱圈中心线任一点拱圈中心线弧长公式和水平拱圈厚度沿弧长变化公式计算得该点径向方向上的拱圈厚度，从而得到半拱圈厚度，两者相减最终得到该点的径向偏距，对应设计坐标也可求得。
如图2所示，点P（X，Z）为任意放样点，求P点与上（下）游设计轮廓线的径向偏距及对应的设计坐标。
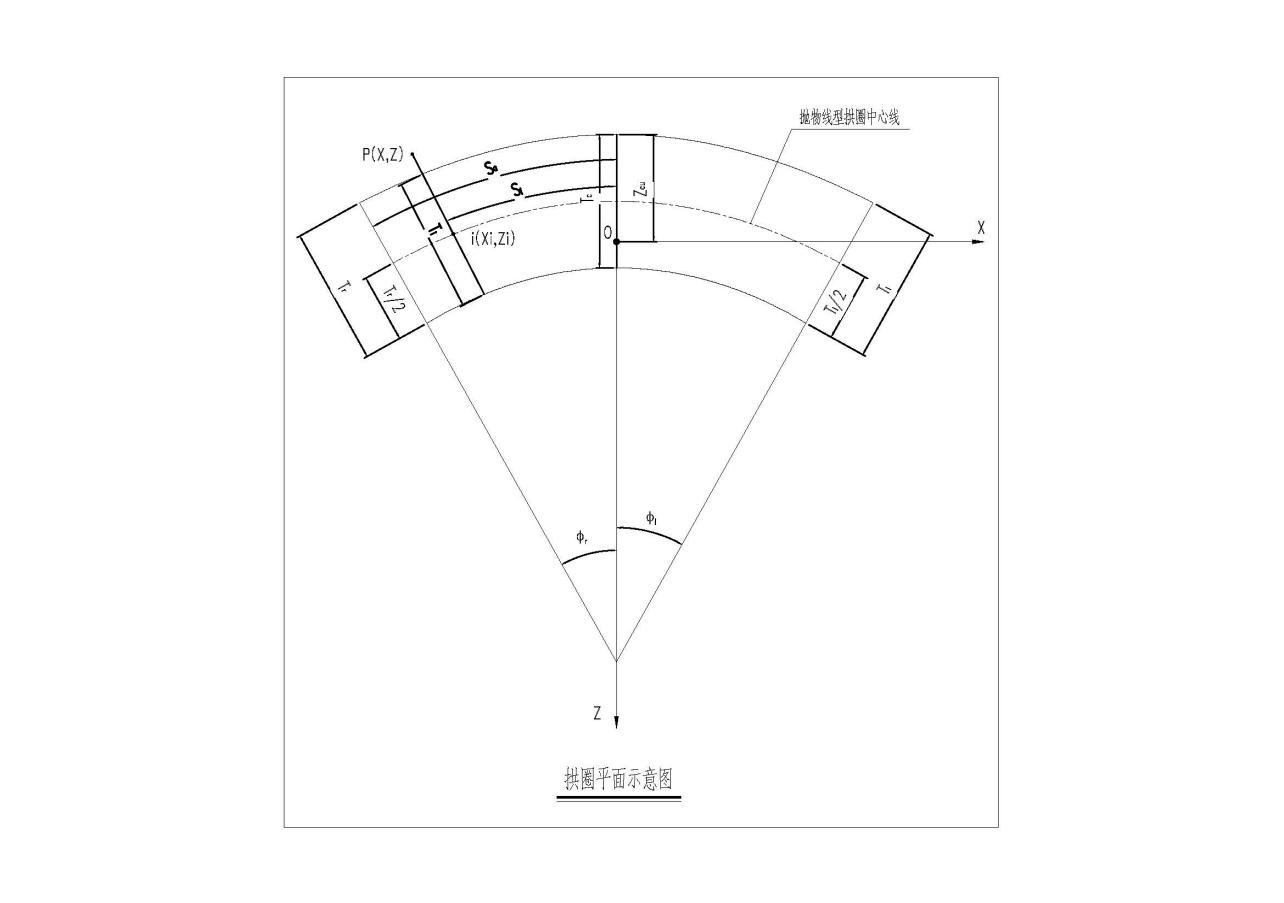
图3 拱圈平面示意图
1）设点I（Xi，Zi）为点P对应抛物线上的垂足，则PI为点P到抛物线的距离。
2）虽然抛物线方程关于拱坝中心线不对称，但由于方程形式一样，可以根据放样点P横坐标X正负提前计算左右岸的抛物线方程系数，后续计算均按对称型抛物线方程处理，为便于编程，根据抛物线的对称性，实际横坐标X均按正值处理。因此根据拱圈中心线参数方程，得出其抛物线方程的一般式为
z=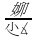
x2+Tc/2+Zcu
3）由直线斜率公式：k=(y2-y1)/(x2-x1)得直线PI的斜率
k1=（Zi-Z）/（Xi-X）
4）由曲线y=f(x)在点(x1，f(x1))处的斜率就是函数f(x)在点x1处的导数，对抛物线方程求导得点I处的斜率
k2=x/R
5）由两条垂直相交直线的斜率相乘积为-1建立方程关系：
k1·k2=-1
6）解方程得Xi3+2R（T/2+Zcu-Y+R）Xi-2R2X=0
此一元三次方程系数p=2R（T/2+Zcu-Y+R），q=-2R2X
由一元三次方程求根公式解得
Zi=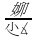 Xi2+Tc/2+Zcu
求出点I坐标（Xi，Zi）
7）由于点I坐标（Xi，Zi）已经求得，根据拱圈中心线任一点拱圈中心线弧长公式和水平拱圈厚度沿弧长变化公式计算得点I径向方向上的拱圈厚度Ti，则点P到上游轮廓线的径向距离
K=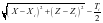
8）根据抛物线参数方程计算得点I对应的半中心角
Φi=arctan（Xi/R）
9）P点对应的上游轮廓线上的设计坐标
X0=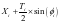
，Z0=
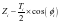
同理如果P点位于下游轮廓线附近，则其对应的下游轮廓线上的设计坐标
X0=
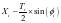，Z0=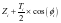
实际编程中利用P点纵坐标Z与对应拱圈中心线上I点纵坐标Zi比较，如果Z>Zi，则判断P点位于下游轮廓线附近，如果Zi，则判断P点位于上游轮廓线附近，再进行对应设计坐标计算。
| Deg：Fix 3 Lbl 1 ?X：?Y：?H：?A -Y→Y H-1947→G -0.358992×10-5G3+0.304409×10-2G2-0.285587G+0.7002×10-7→S -0.126543×10-5G3-0.374475×10-4G2-0.112181G+0.3200×102→T If X≥0：Then -0.350602×10-4G3+0.137792×10-1G2-0.537332G+0.9030×102→R：Else -0.248893×10-4G3+0.105619×10-1G2-0.421068G+0.9820×102→R：IfEnd R×tan(A)→E （X× If X≥0：Then 0.746601×10-5G3-0.203472×10-2G2-0.181831×10-1G+0.3490×102→D：Else 0.183804×10-5G3-0.102940×10-2G2-0.369251×10-1G+0.3461×102→D：IfEnd 2R×（T÷2+S-Y+R）→P：-2R2×X→Q （1÷（2R））×E2+T÷2+S→F tan-1（E÷R）→J （E× T+（D-T）×（L÷C）2.2→B If Y＜F：Then E+（B÷2）×sin（J）→V：F-（B÷2）×cos（J）→W：Else E-（B÷2）×sin（J）→V：F+（B÷2）×cos（J）→W：IfEnd Locate 1,1，”X-PC=”：Locate 6,1，X-V： Locate 1,2，”Y-PC=”：Locate 6,2，Y-W： Locate 1,3，”Ti÷2=”：Locate 6,3，B÷2： Locate 1,4，”R-PC=”：Locate 6,4，K-B÷2◢ Goto 1 |
| 变量 | 说 明 |
| X | 任一点横坐标 |
| Y | 任一点纵坐标 |
| H | 任一点高程 |
| A | 拱端中心线左（右）岸拱端半中心角，单位° |
| G | 高差（H-1947） |
| S | 拱冠梁上游面的Y坐标 |
| T | 拱冠梁处的拱圈厚度 |
| R | 拱冠梁处左（右）岸侧的拱圈中心线曲率半径 |
| M | 拱圈中心线上左（右）岸拱端横坐标 |
| C | 左（右）拱端处对应的拱圈中心线弧长（从拱冠梁起算） |
| L | 拱圈中心线任一点拱圈中心线弧长 |
| D | 左（右）拱端拱圈厚度 |
| B | 拱圈中心线上任一点对应的拱圈厚度 |
| J | 拱圈中心线上任一点对应的半中心角 |
| P | 一元三次方程系数 |
| Q | 一元三次方程系数 |
| E | 任一点对应拱圈中心线上垂足的横坐标 |
| F | 任一点对应拱圈中心线上垂足的纵坐标 |
| V | 任一点对应的上（下）游轮廓线横坐标 |
| W | 任一点对应的上（下）游轮廓线纵坐标 |
| K | 任一点与拱圈中心线的距离 |
1）程序思想：杨房沟水电站拱坝混凝土模板施工测量放样程序可以自动识别放样点的位置范围（左/右岸、上/下游），并随之计算出相应位置的各项参数及变量，进而快速精确的计算出该点对应的上（下）游轮廓线设计坐标及径向偏距，最后利用屏幕显示功能使需要的结果全部同时显示出来。
2）坐标系建立：实际编程过程中将Z方向的反方向设为Y轴正方向，以符合现场施工测量坐标系的建立习惯，X轴正方向为左岸，负方向为右岸，Y轴正方向指向水流上游侧。
3）结果说明：本程序显示结果“X-PC”为横坐标偏差，“Y-PC”为纵坐标偏差，“Ti÷2”为半拱圈厚度，“R-PC”为径向偏差。“X-PC”结果为正值表示X值比设计X0绝对值大，应向绝对值变小方向移动至设计点，反之，则向绝对值变大方向移动至设计点；“Y-PC”结果为正值表示Y值比设计Y0大，应向Y轴负方向移动至设计点，反之，则向Y轴正方向移动至设计点；“R-PC”结果为正值表示实测距离比半拱圈厚度大，应向拱圈中心线方向移动至设计点，反之，则向拱圈轮廓线方向移动至设计点。
4）程序优势：整个程序语法简单、内容简洁、思路清晰，计算结果精确，现场操作简单，解决了拱坝复杂的体形给测量工作带来的计算工作量大，放样效率低的难题。
表2 放样点偏差计算
| 点号 | 程序输入 | 程序输出 | 部位 | ||||||||
| X（m） | Y（m） | H（m） | A（°） | ΔX（m） | ΔY（m） | Ti/2（m） | ΔR（m） | ||||
| 1 | 100.000 | -38.500 | 2102.000 | 38.652 | 0.118 | -0.250 | 4.775 | 0.277 | 左岸上游 | ||
| 2 | 14.000 | -23.000 | 2080.000 | 39.701 | -0.127 | 1.564 | 6.722 | 1.570 | 左岸下游 | ||
| 3 | -15.000 | -2.000 | 2060.000 | 43.082 | 0.012 | -0.122 | 8.517 | 0.123 | 右岸上游 | ||
| 4 | -103.000 | -62.500 | 2040.000 | 44.081 | -0.077 | 0.091 | 11.350 | 0.119 | 右岸下游 | ||
| 5 | 19.000 | 4.000 | 2020.000 | 42.230 | -0.087 | 0.554 | 11.580 | -0.561 | 左岸上游 | ||
| 6 | 68.000 | -47.500 | 2000.000 | 41.651 | 0.208 | -0.258 | 14.259 | -0.331 | 左岸下游 | ||
| 7 | -20.500 | 4.000 | 1980.000 | 39.512 | -0.069 | 0.363 | 14.172 | -0.369 | 右岸上游 | ||
| 8 | -46.000 | -42.000 | 1960.000 | 31.054 | 0.116 | -0.202 | 16.795 | -0.233 | 右岸下游 | ||
| 9 | 0.000 | 0.000 | 1947.000 | 20.051 | 0.000 | 0.000 | 16.000 | 0.000 | 拱冠梁点 | ||
拱坝坝型多，体形复杂，计算浩繁，精度要求高，不同的拱坝体形参数各不相同，相应施工测量放样方法也应灵活多变，只有对程序的编写有非常清晰的的思路才能设计出最佳方案。
本文以杨房沟水电站拱坝混凝土模板施工测量放样为例，详细介绍了拱坝体形参数和相应的程序设计方案，极大程度的提高了现场施工测量放样精度和校模速度，促进了工程进度，减少了测量技术人员及设备的投入，也为处理类似拱坝体形测量放样问题提供了新的解决方案。
参考文献：
[1]王晨阳.解析混凝土抛物线双曲拱坝的施工放样[J].智能城市,2018,4(04):124-125.
[2]彭金明,刘江,杨云,孙富斌,高双阳.混凝土抛物线双曲拱坝的施工放样[J].云南水力发电,2014,30(S1):36-40.
1
客服QQ：30444492琼网文【2021】1550-113号
增值电信业务经营许可证：琼B2-20210322
出版物经营许可证：新出发龙华出字第(2021)009号
广播电视节目制作经营许可证：(琼)字第00779号
版权所有 ©2002-2024 期刊网(www.qikanchina.com) 琼ICP备2021005105号
+R2×sinh-1（X÷R））÷（2R）→C
→E
+R2×sinh-1（E÷R））÷（2R）→L
→K