郑州大学 1.信息与工程学院; 2.教育学院; 3.机械与动力工程学院,河南郑州 450000
摘要
近来,我国医疗体系得到快速发展,居民的健康意识也随之增强,然而,由于我国人口基数较大且老年人口所占比例逐渐提高,“排队难”问题成为医院门诊的常见现象。针对这一问题,本文利用排队论量化分析当前医院的排队系统,根据病人的到达情况拟化泊松流,建立了病人检查服务系统的M/M/S模型,通过Matlb得到结果并进行验证,最后,向医院提出建议。
关键词:排队论、泊松流、医院排队
背景
中国自改革开放以来,经济社会快速发展,居民的收入水平不断提高,医疗卫生条件也得到极大改善。居民健康意识的增强使得居民对医疗健康的要求也逐步提升,但是我国人口基数比较大,虽然近来中国医疗卫生领域发展迅速,然而在管理和运营方面仍有很大的提升空间,“排队费时,挂号费力”成为医院的普遍情况。
据国家数据官网显示,2018年全国医疗机构总数为997433个,其中医院有33009个,而一年的入院人数有20016.95万人,诊疗人数更是达到了35.77亿人次。受到现实情况制约,大多数医院的成本、设施和人员等客观条件是难以改变的,无法轻易增加设备和人员,适应和配合病人的需求变化,因此病人在医疗服务过程中的排队等待现象是难以避免的。所以,通过某些手段尽量缩减病人的等待时间,尽可能地满足病人地需求,提高医疗卫生领域的运行效率,对公众和医院都具有重要的现实意义。
对于医院排队问题的研究,国内学者角度各有差异,不过排队论模型作为这类问题的经典模型,得到广泛使用。北京大学肿瘤医院的学者王楠和武爱文采用了M/D/1和M/G/1两种排队模型,计算多种组合模式,着重根据病人的排队等待时间进行模型的模拟计算和分析i。刘胧、卞齐昊等学者根据排队论经验设定医院排队模型分布类型,运用卡方检验进行验证,确定医院排队模型最终分布类型,计算出医院排队模型地队长、等待时间等因素,最终通过Witness仿真软件对医院排队及服务模型进行仿真分析,为医院决策提供了依据ii。除此之外,学者周宁、于华等人以评估医疗救助能力的排队论模型为例,提出了应对生化恐怖袭击的非稳态系统的建模和求解方法,建立了适合生化恐怖袭击事件特性的多库决策支持系统结构,将有关生化恐怖袭击事件处置的模型和算法集成到系统中,验证了系统的可行性和实用性。iii
不同类型的病人需要在医院进行不同的检查,不同的检查分布在不同的地点,同时,医院的各个科室分布比较分散,对于不熟悉医院服务流程的病人来说,不得不在各个科室、收费窗口之间往返,消耗了病人的时间和体力。
出现以上现象的原因在于,病人的需求和医院服务能力之间的不平衡,病人的需求时间与可获得服务的不匹配。若病人没有需求,则医院的服务能力便会丧失;若医院需求过大,就会超出医院服务能力,出现病人排队等待的现象。
根据医院的排队现状,本文分别建立了检查病人到达时间和治疗时间的相关模型,利用排队论算法归纳出检查服务系统模型,对模型的相关数据进行仿真分析,并对模型进行拟合和优化,最终得出最优解。
方法:排队论模型建立
排队论模型是基于随机服务系统理论的数学模型,是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法,属于运筹学的一个分支。排队系统包括三个组成部分:输入过程、排队规则和服务机构。服务对象的到来时刻和对他们的服务时间,即占用服务系统的时间都是随机的。排队系统模型的示意图如下: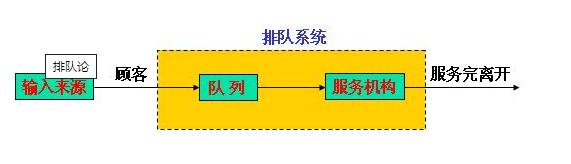
本文运用排队论模型来衡量医院门诊服务流程的效率,主要研究服务排队时间和服务规则对病人的影响,并对排队流程进行优化,使病人排队时间的消耗最小化。
首先建立病人到达时间间隔分布模型:泊松分布和泊松流。
如果病人的到达时间满足以下条件,本文将病人的到达分布称之为泊松流:
(1)在不重叠的时间间隔内,到达的病人数量是相互独立的。
(2)对于足够小的时间间隔[t,t+ t],到达客户的概率与t无关,但仅与时间间隔成比例(稳定性):P1(t,t +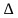 t) =
t) = 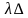 t + o(
t + o(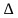 t)
t)
(3)对于足够小的时间间隔[t,t+ t],两个或更多病人到达的概率可以忽略不计(一致性)。
泊松流的到达间隔服从负指数分布,如果病人到达时间间隔T的概率密度为:
fT ( t) =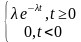
T服从负指数分布,分布函数为:
FT(t)=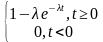
如果病人流是泊松流,病人到达的时间间隔服从上述负指数分布:
E[T] = 1/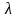 ; Var[T] = 1/
; Var[T] = 1/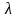 2;
2; 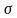 [T] = 1/
[T] = 1/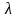
病人服务时间分配:
病人服务时间等于两个相邻病人离开排队系统的时间间隔。如果其服从负指数分布,其概率密度和分布函数为:
fTs ( t) = 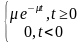
FTs (t)=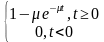
那么,
E[Ts]= 1/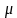 ;Var[Ts]= 1/
;Var[Ts]= 1/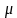 2;
2;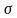 [Ts]=1/
[Ts]=1/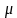
M/M/S模式:
这种模式与M/M/1模式的区别在于有S服务台,它们的工作相互独立,服务率相等iv。如果病人到达,S的服务台都处于忙碌状态,那么他们将排队等候,采用先来先服务的单队列模式。
整个系统的平均服务率为: s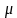 ,
,
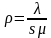 ,(
,(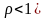 是系统的服务强度。
是系统的服务强度。
这里本文得出一些公式:
状态概率:
P0=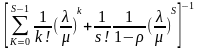
Pn=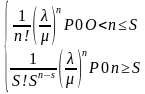
主要经营指标:
Lq=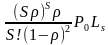 =
=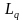 +s
+s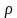 Wq=
Wq=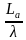 Ws=
Ws=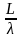 =Wq+
=Wq+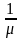
系统状态的概率N>=S:
P ( N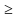 k) =
k) = 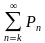 =
=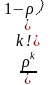
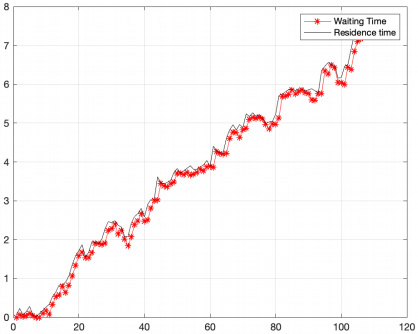
将建立的模型通过Matlab进行验证,得到结果如下,由图表可知,模型建立合理,具有较高的精确度。
结论
根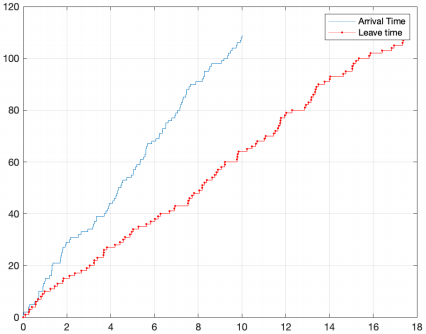
据模型结果,为了缓解各个医院挂号过程中的排队问题,缩短病人的排队时间,不仅需要医院科学配置窗口服务人员,做好引导标识,让病人快速熟悉医院科室位置,而且需要病人的积极配合,尽量不在就诊高峰期到医院,减少拥堵的可能性。
总而言之,缓解排队难问题最有效的办法是增加服务窗口,不过考虑到医院人员成本和建筑的限制,这不是最优解,同时,需要考虑到,随着中国人口的增加和老年人口占比的提高,未来到医院的就诊人次和排队时长很可能会更多,情况只会更加严重。因此,减化门诊步骤,缩短流程,提高办事效率是医院应该考虑的重点。
本文在对国内排队论研究进行总结的基础上v,立足于病人等待时间,及时就诊进度的需求和现有排队系统难以解决的全流程排队,应用排队论模型和Matlb等统计软件,建立了病人的检查服务系统模型,并对 模型的适用性和可靠程度进行检验。根据模型结果,本文结合目前大中型医院现有的就诊流程提出了可行的应对策略,为缓解医院排队问题提供了参考。
i 王楠,武爱文.运用M/D/1和M/G/1排队模型配置医院门诊收费窗口资源[J].中国卫生统计,2015,32(04):680-682.
ii刘胧,卞齐昊,李萍.运用WITNESS的医院排队模型仿真[J].工业工程,2010,13(02):73-75+97.
iii周宁,于华,隋杰.排队论在生化恐怖袭击的医疗救助中的决策支持[J].计算机系统应用,2009,18(09):112-115.
iv孙梅.排队论在医院门诊收费管理中的应用[J].科技视界,2016(10):22-24.
v邓惠霖.排队论模型在门诊挂号室人员配置中的应用[J].世界最新医学信息文摘,2019,19(29):181+186.