华北水利水电大学 河南省郑州市 450045
摘要:为了更加准确地对电压波动与闪变进行检测分析,本文利用变分模态分解(VMD)对电压波动与闪变信号进行检测。选取典型的电压闪变算例,运用VMD算法对信号进行分析,然后利用傅里叶变换检测出瞬时频率和幅值的关系。验证了VMD算法可以作为检测出电压波动与闪变的新方法。由于VMD算法对噪音具有鲁棒性,所以通过利用VMD和局部均值分解算法(LMD)算法分别对含有噪音的闪变信号进行分析,可以清晰的对比出VMD算法在对含有噪音的信号检测时更加准确。
关键词:电压闪变,变分模态分解,噪音
0 引言
随着社会发展越来越迅速,冲击性、波动性的负荷不断增多,导致配电网中的电压波动与闪变也越来越严重。为了检测这一种电能质量,出现了各种各样的方法用来检测电压波动与闪变[1]。文献[2]利用EMD(经验模式分解)方法可以准确检测到电压波动与闪变发生的时刻和终止时刻。但是,EMD缺乏严格的数学理论,易受模式混合、端点效应影响。文献[3]利用LMD(局部均值分解)用平均滑动法拟合包络,避免了过包络和欠包络,所求频率是具有物理意义的正值。但是很容易受模式混合效应和噪音影响。
2014年Dragomiretskiy和 Zosso提岀了变分模态分解VMD。VMD 有坚实的理论基础,可以在抗噪性、频率相近信号的模态分离和重构信号方面表现出优异的性能。本文分别采用 VMD和LMD对电压波动与闪变含噪信号进行分析,通过傅里叶变换提取各模态的瞬时幅值和频率进行对比分析,证明所提方法的准确性和优越性。
1 VMD的基本原理
1.1 VMD基本原理
VMD的核心思想是频域稀疏性。VMD将信号x(t)分解成IMF的集合,其围绕它们各自的中心频率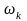 进行频带限制,同时最佳地重构信号。它迭代地更新频域中的每个IMF,然后将中心频率
进行频带限制,同时最佳地重构信号。它迭代地更新频域中的每个IMF,然后将中心频率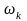 估计为IMF功率谱的重心。将模式的频谱转换为“基带”,通过与指数估计的相应频率进行混合。最后,可以通过梯度的平方
估计为IMF功率谱的重心。将模式的频谱转换为“基带”,通过与指数估计的相应频率进行混合。最后,可以通过梯度的平方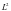 范数来估计带宽。由此产生的约束变分问题是:
范数来估计带宽。由此产生的约束变分问题是:
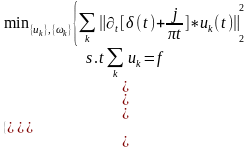 (1-1)
(1-1)
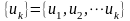 和
和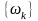 =
=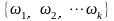 分别为所有模式集合及其中心频率的简写符号。同样,
分别为所有模式集合及其中心频率的简写符号。同样,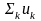 为所有模式的总和。为了使变分问题不受约束,此处使用二次惩罚因子和拉格朗日乘子。二次惩罚是提升重建逼真度的典型方法,通常在高斯噪声存在的情况下。另一方面,拉格朗日乘数是严格执行约束的常用方式。引入增广的拉格朗日如下:
为所有模式的总和。为了使变分问题不受约束,此处使用二次惩罚因子和拉格朗日乘子。二次惩罚是提升重建逼真度的典型方法,通常在高斯噪声存在的情况下。另一方面,拉格朗日乘数是严格执行约束的常用方式。引入增广的拉格朗日如下:
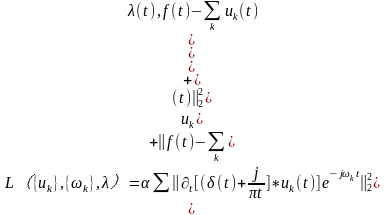 (1-2)
(1-2)
上述变分问题被等同为迭代子优化序列中的寻找增广拉格朗日量的鞍点,在VMD中称为乘法器的交替方向法,即通过将模式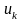 更新来解决这一问题。
更新来解决这一问题。
为了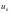 更新我们可以等效于求解公式(1-7)的最小化问题:
更新我们可以等效于求解公式(1-7)的最小化问题:
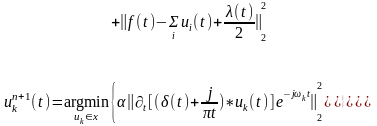 (1-3)
(1-3)
现在,利用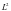 范数下的 Parseval/ Plancherel傅里叶等距将这个问题在频域中解决:
范数下的 Parseval/ Plancherel傅里叶等距将这个问题在频域中解决:
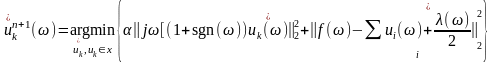 (1-4)
(1-4)
现在在第一项中进行变量变更: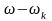 代替
代替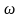 ,则有:
,则有:
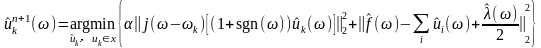 (1-5)
(1-5)
对于正频率而言,令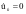 ,可以得到这个二次优化问题的解为:
,可以得到这个二次优化问题的解为:
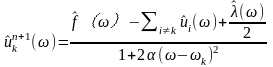 (1-6)
(1-6)
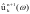 是当前残差的维纳滤波,信号在
是当前残差的维纳滤波,信号在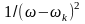 之前,然后通过 Hermitian对称可以获得实模的全频谱。而时域模式可以用该滤波分析信号的傅立叶逆变换的实部获得。
之前,然后通过 Hermitian对称可以获得实模的全频谱。而时域模式可以用该滤波分析信号的傅立叶逆变换的实部获得。
这个二次优化问题中心频率的解为:
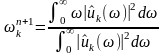 (1-7)
(1-7)
2 算例仿真
2.1 单频闪变信号检测
设定闪变信号的参数如下:调幅波幅值为工频载波电压幅值的10%,频率为10Hz,载波频率为50Hz,初相为0,采样频率为1000Hz,采样时间为1s。
设定的信号如式(3-1)所示:
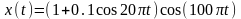 (3-1)
(3-1)
如图1所示,是x(t)为10Hz的单频电压波动信号(纵轴为标幺值),图2为VMD分解出来的3个AM-FM分量,其中a为基波,b为调幅波,c为残波。图3是利用VMD算法检测出来的频谱图,由图中数据可知,这种方法可以准确的检测出来闪变信号数据,其中检测闪变信号的幅值为0.09712pu和频率为10Hz,和理论值一致。证明了VMD方法可以有效的检测出闪变信号。
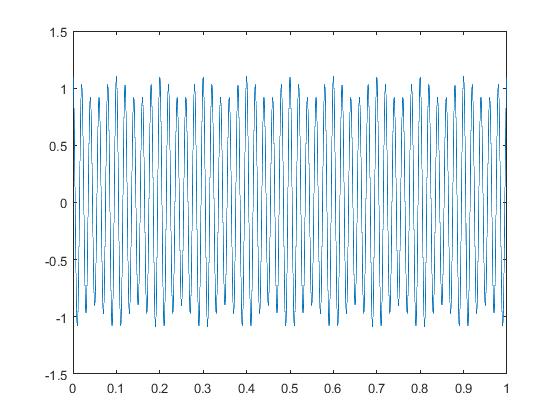
图1 单频率的闪变信号
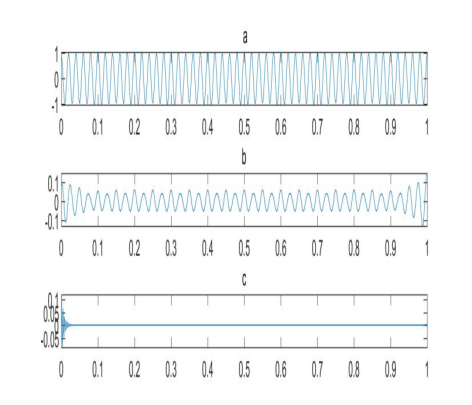
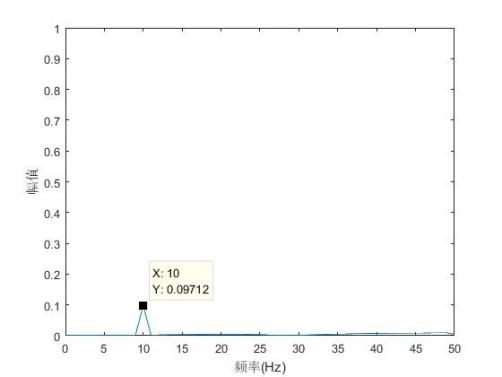
图2 AM-FM分量图 图3 傅里叶检测出的闪变频率和幅值
2.2 含噪音信号的仿真
在原有的单频闪变信号上加入白噪音,所有的参数和本文中的单频闪变信号一致。
如图10所示,是添加白噪音后的电压波形图。图11是利用VMD算法对噪音信号进行去噪后的波形和不含噪音的单频闪变信号的对比图,从图中可以清晰的看出两条波形基本重叠在一起。如图12所示,是关于LMD算法对含噪信号进行的检测和不含噪音的单频闪变信号检测的对比图,从图中可以看出两条波形有明显的不同,说明LMD算法不能有效的检测含噪信号。如图13所示是两种办法检测的频谱图对比,从图中可以清晰的看出LMD算法对含噪信号检测的局限性,也进一步验证了VMD算法在去除噪音上的有效性和准确性。
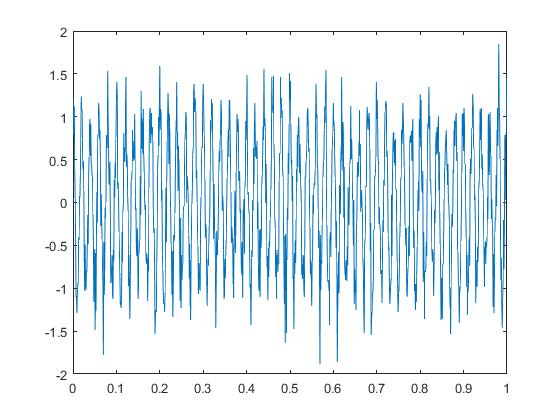
图4 含白噪音的电压闪变信号
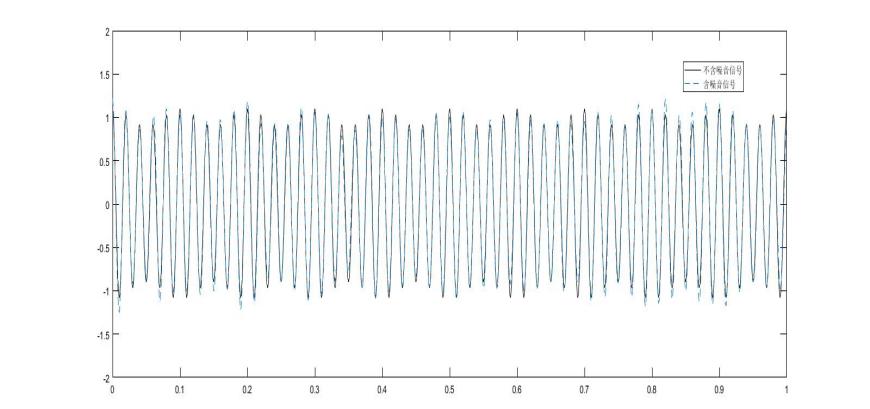
图5 VMD检测出的电压闪变信号对比图
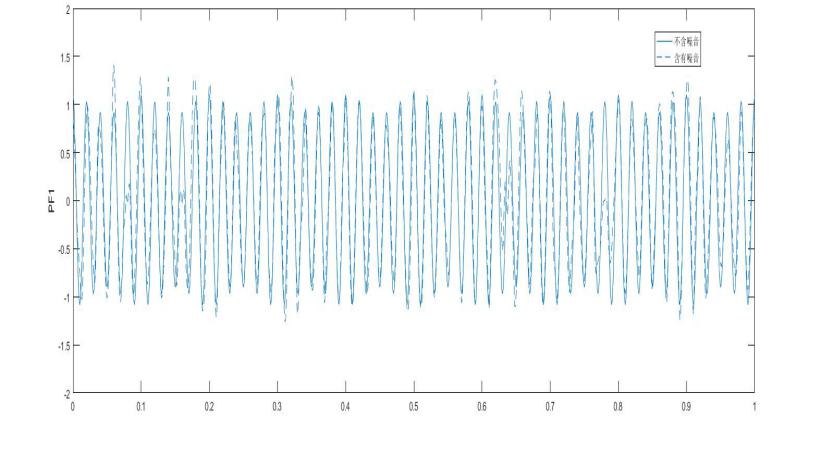
图6 LMD检测的电压闪变信号对比图
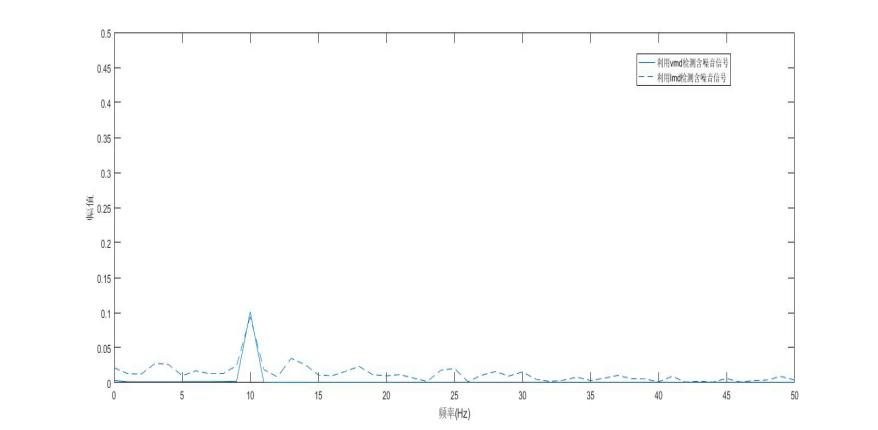
图7 两种方法对含噪信号检测的频谱图对比
3 总结
VMD将复杂信号分解为特定数量的IMF,这些IMF本质上是AM-FM信号,因此可以估计它们的瞬时幅度和瞬时频率。所以非常适合用于电压波动与闪变的信号分析中。更重要的是,VMD的非递归和并发分解特性有效地避免了递归分解算法的缺点,例如对噪声和釆样的敏感性,相比于LMD算法有更加严格的数学理论支撑和更加有效的去除噪音作用。
参考文献:
[1]程浩忠,艾芊,张志刚等电能质量北京:清华大学出版社,2007
[2]刘稳坚,黄纯,邢耀广,武艳华.经验模态分解及Hilbert谱分析在电压闪变检测中的应用[J].计算机测量与控制,2006(06):707-709+756.
[3]胡晓波,杜娟丽.基于LMD算法的电压闪变参数识别新方法[J].河南科学,2016,34(05):721-725.