广东省 惠州市 惠东县 实验小学 广东 惠州 516300
摘要:在小学低段学习中,学生会通过实际操作和利用图形建立丰富的表象。到了中高级阶段的学习时,实际动手操作环节的减少,以及文字语言和符号语言的复杂,让很多学生对数学失去了兴趣。而利用“画数学”策略就好像为学生打开一条便利的通道,使学生原本认为刻板的、枯燥的文字或符号变成鲜活生动、有趣的图形,从而提高学生学习数学的热情,并达到快速、正确解决问题的目的。因此,让学生掌握画图这种策略在数学教学中是很重要的。
关键词:计算数学;分数意义;分数算式;分数应用题
小学数学里,分数的学习是一个非常重要的知识点。在教学过程中,我常常有这样的感触:即便学生能把一些题目做出来,但对解题的思路和过程却说不清楚,而且越说越糊涂,教师如果仅凭语言分析,学生依然入坠五里云雾。那该如何帮助学生找到突破口,打开思路呢?画图,它如一座桥梁,让学生把图当成“有形”的语言,把想法说出来,把思路理清楚,从而顺利解决数学问题。
为此,我着重在分数知识点的教学中尝试运用“画数学”的方法,现与大家一同分享。
画分数——不知不觉中感悟分数意义
分数是个相对复杂的概念,它是在学生认识了整数、小数的基础上再延伸的知识点,在初学阶段,学生对分数意义的摸索和学习往往需要一个较长的过程来适应。因此在教学过程中渗透“画数学”的思想,可以帮助学生快速掌握分数的意义。例如:在初步理解分数意义的基础上,比较分数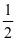 和
和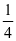 ,教学时班上的学生出现了两个声音,在听取学生真实想法的背后就暴露出他们对分数的概念是模糊的、一知半解的。这时,我及时引导学生根据分数的意义,并通过画同样大小的长方形、圆形来表示出这两个分数。学生饶有兴趣的选择自己喜欢的画图方式表示出该两个分数,如图一、学生通过画图后,答案便不攻自破。然后再通过几组数据比较发现同分母分数相比较时或同分子分数相比较时的法则。
,教学时班上的学生出现了两个声音,在听取学生真实想法的背后就暴露出他们对分数的概念是模糊的、一知半解的。这时,我及时引导学生根据分数的意义,并通过画同样大小的长方形、圆形来表示出这两个分数。学生饶有兴趣的选择自己喜欢的画图方式表示出该两个分数,如图一、学生通过画图后,答案便不攻自破。然后再通过几组数据比较发现同分母分数相比较时或同分子分数相比较时的法则。

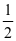
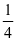
(图一)
画算式——轻轻松松中理解分数算理
数学算式是将数学问题进行高度概括后抽象出来的语言,但这个总结的过程对学生来说是困难的、枯燥的,形如再初学同分母分数加法计算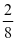 +
+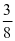 等于多少?学生仅凭算式表面的结构会天真的说出答案
等于多少?学生仅凭算式表面的结构会天真的说出答案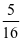 ,若在这个教学过程中,老师又只局限于算式符号的求解,只教学生同分母分数相加时,分母不变,分子相加这个算法而不教学生寻求真正的算理,学生就变成只懂求解答案而不知其意义,在以后的学习中就会缺乏知识的主动探索和钻研。因此,分数算式教学中通过让学生主动把抽象的符号语言转化成形象的图,引导学生在画图过程中不仅知道怎么算,也明白其中算理,从而亲身体会数学的魅力后便充满兴趣往下一个阶段学习分数乘法算式做准备,例如:
,若在这个教学过程中,老师又只局限于算式符号的求解,只教学生同分母分数相加时,分母不变,分子相加这个算法而不教学生寻求真正的算理,学生就变成只懂求解答案而不知其意义,在以后的学习中就会缺乏知识的主动探索和钻研。因此,分数算式教学中通过让学生主动把抽象的符号语言转化成形象的图,引导学生在画图过程中不仅知道怎么算,也明白其中算理,从而亲身体会数学的魅力后便充满兴趣往下一个阶段学习分数乘法算式做准备,例如: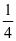 ×
×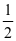 等于多少?首先我们已经了解了该算式的意义就是“
等于多少?首先我们已经了解了该算式的意义就是“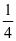 的
的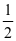 是多少”,然后可以用一个长方形当成单位“1”,画出长方形的
是多少”,然后可以用一个长方形当成单位“1”,画出长方形的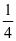 ,然后把
,然后把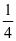 的部分再平均分成2份,取其中的1份,这样我们就可以得出,取出的那一份就是整个长方形的
的部分再平均分成2份,取其中的1份,这样我们就可以得出,取出的那一份就是整个长方形的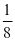 。
。
学生在分数乘法初始阶段学习的过程中已经尝到了“甜头”,干劲十足,接下来也饶有兴趣的运用画图方式解决下一个难题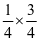 。尽管有小部份学生在这道题第二步,把其中
。尽管有小部份学生在这道题第二步,把其中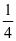 的部份如何再分成
的部份如何再分成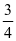 时遇到困难,但是当我交由班里思维较敏捷的学生来当“小老师”演示一遍后都能恍然大悟,快速在脑海里反应过来,即便是后进生也能在解开心中的谜团后心里美滋滋的笑了。第一步依旧先用一个长方形当成单位“1”,画出长方形的
时遇到困难,但是当我交由班里思维较敏捷的学生来当“小老师”演示一遍后都能恍然大悟,快速在脑海里反应过来,即便是后进生也能在解开心中的谜团后心里美滋滋的笑了。第一步依旧先用一个长方形当成单位“1”,画出长方形的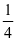 ,然后把
,然后把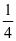 的部分再平均分成4份,取其中的3份,也就是整个长方形的
的部分再平均分成4份,取其中的3份,也就是整个长方形的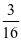 。画图过程如图2。学生在分数算式的学习过程中,通过独立思考、动手画图、同伴帮扶,整节课下来学生在轻松愉悦的课堂气氛中学到知识,课堂效率也大大提高。
。画图过程如图2。学生在分数算式的学习过程中,通过独立思考、动手画图、同伴帮扶,整节课下来学生在轻松愉悦的课堂气氛中学到知识,课堂效率也大大提高。


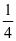 的
的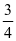 是
是
 整个长方
整个长方
形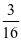
长方形的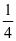
(图2)
画题意——轻而易举地解决分数应用题
苏霍姆林斯基说:“如果哪个孩子学会了画应用题,我就可以有把握地说,他一定学会解决应用题。”然而,在小学阶段让孩子最头疼的一种题型就是解决问题,他们常常对数量关系理不清,分数应用题更是容易把学生“吓”住了。因此,要锻炼学生习惯的在列算式前把题目意思用图的形式画出来,然后在文字语言转化成图形语言的过程中进行思考,数量关系便顺理成章的理清了。例如在学习分数乘法应用题时,我先给学生出示题目“三(3)班植了32棵树,三(4)班植树的棵树比三(3)班的多4棵,三(4)班植树多少棵?”学生很自信的一下子就解决出来了。接着我把题目的多4棵改成多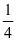 ,有部分学生依然自信的回答32加
,有部分学生依然自信的回答32加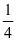 等于
等于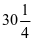 。可部分学生就质疑到树怎么会有
。可部分学生就质疑到树怎么会有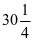 棵呢?在我的鼓励下,我让学生借助画图展现出三(3)班和三(4)班植树棵树的关系,帮助学生找到解题思路。 通过画图,学生很清晰的可以看出多出的部分相当于三(3)班
棵呢?在我的鼓励下,我让学生借助画图展现出三(3)班和三(4)班植树棵树的关系,帮助学生找到解题思路。 通过画图,学生很清晰的可以看出多出的部分相当于三(3)班
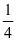 ,则是8棵,所以三(4)班植树是40棵。
,则是8棵,所以三(4)班植树是40棵。
在这个教学环节,我通过变题,不露痕迹地沟通新旧知识的联系,又从文字到画图,让学生轻轻松松的突破“多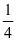 ”的难点,也使原本被老师们诟病“语言表达能力薄弱”“数学课上一言不发”的学生在本节课上像换了一个人,他们能够拿着自己的作品上台有条理地跟同学分享自己的思考,为什么会这样?我想应该是“画数学”为学生提供了数学学习的拐杖,为他们搭建了自主探究和展示的平台,有了“画数学”,原本抽象的算理变得直观,原本难以把握的思路变得有迹可循了。
”的难点,也使原本被老师们诟病“语言表达能力薄弱”“数学课上一言不发”的学生在本节课上像换了一个人,他们能够拿着自己的作品上台有条理地跟同学分享自己的思考,为什么会这样?我想应该是“画数学”为学生提供了数学学习的拐杖,为他们搭建了自主探究和展示的平台,有了“画数学”,原本抽象的算理变得直观,原本难以把握的思路变得有迹可循了。
经过不同年级的执教,同学们用“画数学”这种学习方法来解决分数问题时,不仅体会到数学学习的乐趣,我也在“画数学”教学中体会到它的魅力。因为它不但可以使复杂的分数问题迎刃而解,而且在解决问题的过程中有效的锻炼了学生的思维能力。在这一思想与方法的导引下,它让老师教的简单,学生学得轻松,这也是我所追求的数学课堂。
参考文献
【1】叶建云.可以这样教数学.华东师范大学出版社.2012年8月.
【2】戴曙光.简单教数学.华东师范大学出版社.2012年10月.

1