贵州省瓮安中学 贵州瓮安 550400
摘 要:高考数学冲刺复习,目的是帮助学生快速找到适应学生系统复习的方法,提供学生的解题能力与技巧。总之,学生注重课本、敢于取舍、熟记重要结论,掌握基本题型、牢记必备解答知识点、调整好心态,争取在高考中给自己一个完美的答案。
关键词:高考;冲刺;训练;高中数学
作为一名高中学生,高考冲刺阶段的应试训练非常重要。但很多学生都在这阶段变得茫然,找不准定位和方向,特别是课堂上,平时考五六十分的学生,往往又是二本的边缘生,差就差在数学上。每年高考分数出来以后,就埋怨自己如果数学能多考10多分或者20多分,就能上二本了,自己有这个能力,却没有拿到相应的分数,导致自己与二本擦肩而过,成为自己一生的遗憾。有的学生就此与高校无缘,有的学生就会为此再奋斗一年,有的只能读专科或者高职院校。错过了更理想的升学机会。针对该类学生,本人提出如下学习建议,供大家探讨:
强化课本基础知识,掌握最基础的概念、性质、公理、定义等
熟悉数学的基础概念、性质、公理、定义等,可以通过简单的运算及相应的数学知识,快速地处理一般难度的选择填空题,做到心中有数。做到会的,坚决完成,不能因为马虎导致细节性的错误。
例 1(19高考)已知集合A={-1,0,1,2},B={x|x2≤1},则A∩B=( )。
{-1,0,1} B.{0,1} C.{-1,1} D.{0,1,2}
分析:本题基本上知识点都会,平时也不会出错,但高考中容易忽视B={x|x2≤1}中含0而导致错误。注意注意结合与不等式的性质,容易得出正确答案A。
例 2(18高考)(1+i)(2-i)=( )。
-3-i B.-3+i C.3-i D.3+i
分析:复数知识点,几乎年年都要考。其实都不难,毕竟关于常考的内容就是化简、求模、求共轭、求实部、虚不等,但得分率仍然不高,就是简单内容,学生容易忽视基础,忽视概念及性质而导致错误。只要注意概念、性质、公理、定义,就容易得出正确答案D。
二、敢于取舍,果断放弃不会的东西。
有的学生老是认为,有的选择填空题,一定比后面的大题容易得分,结果都是A、B、C、D之一,总是想算出正确的答案,而且常规方法又会,但就是运算量特别大。费时费力,还容易出错,导致没有时间看后面的大题,导致隐性失分。只要做对8-10题,实在复杂的,该猜及猜,该蒙则蒙,至少为后面大题节约了时间,可能能补回来。
例 1(18高考)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9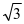 ,则三棱锥D-ABC体积的最大值为( )
,则三棱锥D-ABC体积的最大值为( )
12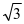 B. 18
B. 18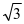 C. 24
C. 24 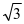 D.54
D.54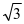
分析:本题考查球的性质、空间几何体的体积。直接猜吧,还有25%的机会,避免浪费时间,造成隐形失分,不值。
一般遇到这样的填空题,对应平时考试就不高的学生,能够及时的选择缓一缓或者放弃,先看看后面的大题,能否写一写,先争取搞到点步骤分再说,可能是最理想的做法。因为选择填空题,对就对,错就错,没有思路、步骤分可言。
三、记住一些课本证明后恒成立的结论,直接书写应用
比如圆锥曲线的焦点三角形的面积,焦点弦长等,学生不记课本练习题中证明了的二级结论,导致花大量时间计算,同时容易出错。其实,选择填空题,是不需要过程的,如果学生能记住课本练习题中证明了的二级结论,直接应用,不仅节约时间,还不容易出错,大大提高正确率。
记住圆锥曲线中焦半径、焦点弦、焦点三角形相关二级结论:
推导1:当曲线为椭圆或双曲线时|AB|=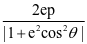 ,当曲线为抛物线时,|AB|=
,当曲线为抛物线时,|AB|=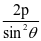 。
。
推导2:当曲线为抛物线时,较长焦半径|AF|=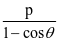 ,较短焦半径|BF|=
,较短焦半径|BF|=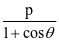 ,焦点弦的弦长公式为|AB|=
,焦点弦的弦长公式为|AB|=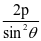 。
。
推导3:设d为原点到直线的距离,A和B为抛物线上的两点,则d=|OF|sin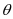 =
=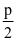 sin
sin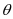 ,
,
S△AOB=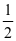 AB
AB d=
d=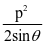 。
。
已知点F是离心率为e的圆锥曲线C的焦点,过点F的弦AB与C的焦点所在轴的夹角为θ,则有:
1.若AF=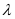 BF(
BF(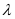 ≥0)则焦点在x轴上时,有|ecos
≥0)则焦点在x轴上时,有|ecos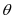 |=|
|=|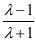 |;若已知斜率为k,焦点在x轴上时,则有e=
|;若已知斜率为k,焦点在x轴上时,则有e=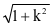 |
|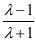 |,若已知斜率为k,焦点在y轴上时,则有e=
|,若已知斜率为k,焦点在y轴上时,则有e=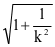 |
|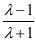 |。
|。
2.椭圆的两个焦点为F1,F2,直线L过F2且与椭圆相交于两点A,B,则△F1AB的周长为4a;
3.椭圆焦点分别为F1、F2,点P是椭圆上任意一点,∠F1PF2=θ,则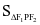 =b2tan
=b2tan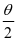 .
.
4.双曲线焦点分别为F1、F2,点P是双曲线上任意一点,∠F1PF2=θ,则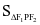 =b2/tan
=b2/tan
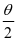 .
.
例1:(2014年高考)设F为抛物线C:y2=3x的焦点,过点F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为( )
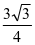 B.
B. 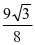 C.
C.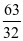 D.
D. 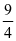
分析:如果能记住相关焦半径知识,用公式S△AOB=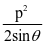 =
=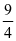 直接算,就很容易得出正确答案.例2:(2018年高考)设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线L与C交于A,B两点,|AB|=8。
直接算,就很容易得出正确答案.例2:(2018年高考)设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线L与C交于A,B两点,|AB|=8。
(I)求L的方程;(Ⅱ)求过点A,B且与C的准线相切的圆的方程。
分析:常规解法:
由题意得F(1,0),L的方程为y=k(x-1)(k>0),设A(x1,y1),B(x2,y2)
由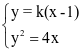 ,得k2x2-(2k2+4)x+k2=0.△=16k2+16>0,故x1+x2=
,得k2x2-(2k2+4)x+k2=0.△=16k2+16>0,故x1+x2=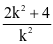 .
.
所以|AB|=|AF|+|BF|=(x1+1)+(x2+1)=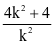 .由题设知
.由题设知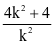 =8,解得k=-1(舍去),k=1因此l的方程为y=x-1.
=8,解得k=-1(舍去),k=1因此l的方程为y=x-1.
但如果用二级结论解,直接设AB倾斜角为θ,则tanθ=k>0.由|AB|=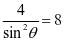 ,的sinθ=
,的sinθ=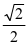 ,tanθ=
,tanθ=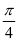 ,则L直线方程为y=x-1.就简单得多了。
,则L直线方程为y=x-1.就简单得多了。
(Ⅱ)省略。
四、熟悉近年高考大题题型 写出必用知识点 争取得分
大部分学生平时训练写出了知识点,但老师没有评分,但高考是要给学生具体评分的。所以,很多学生,由于前面选择填空花费时间较多,导致大部分学生忽略掉简答题,甚至连送分的知识点也不写。其实高考,的确是差一分也会让人计无所出,何况是十几二十分呢?比如:解三角形题目:正弦定理、余弦定理、三角形内角和定理,基本上都会用到,即使不会完整的解答,也应该根据题意写出基本答案,但很多同学自认为写了也没用,真的很可惜。同理,圆锥曲线,很多同学都清楚标准形式及轴与焦点、离心率之间的关系,有的学生觉得无法写出完整的答案,干脆就不写了,类似丢分现象比比皆是。
学生一定要记住,把自己学到的知识点尽可能的多写,哪怕是模糊的记忆也要尽全力去争取,平时学习当中分数只是手段,不是目的,但高考绝对是到了分分必争的最关键时刻,也是决定你未来的一个重要环节。
逝者不可谏,来者犹可追,所以无论什么样的题型都不要轻易放弃。
五、调整好心态 控制好试卷解答分值与时间比
坚决集中精力拿到选择题8-10个,填空题争取2-3个,简答题自己必须突破1-2题满分题型,1-2题拿4-8分题型,1-2题拿2-4分题型。这样,基本上能考八九十分。但有的学生没有信心,没有整体概念,好高骛远,不关注课本基础知识和细节,往往训练后又不及时总结,导致最后冲刺训练效果不突出,形成考后无效果或效果不明显。没有规范知识点的书写要求,造成会的也没时间写,或者认为没必要写、写了也没分,这是隐性失分最致命的原因。
总之,高考冲刺训练,练的是基础、是心态、是取舍、是答题的技能和技巧,力争高考有突破,让学生取得理想的高考成绩!就需要学生在最后的冲刺阶段,灵活运用已经证明过的二级数学结论,能使很多问题的解答与运算简单得多,也能起到事半功倍的效果。
参考文献:
薛金星 中学教材全解 2018版
廖耿丰.高考数学题型与技巧 2020年版
最新五年高考真题汇编详解.数学 2019年6月版