中车唐山机车车辆有限公司 河北省唐山市 064000
摘要:在地铁车辆进行关于维护工作的决策过程中,公司各部门会为各自想要得到的隐形利益进行竞争,文章结合了地铁车辆设备的动态衰退规律,采用非完美维护策略,通过设备阶段性衰退的故障率建立了函数模型,以此来对车辆设备预防性维护计划的影响因素进行分析,对隐形竞争对其的影响程度开展探讨。以动态博弈理论为基础,将运营部门和维护部门设计成博弈参与对象,将两个部门都建立了具有优先性质的博弈模型,利用逆向归纳法对博弈模型的纳什均衡解进行解答。求得的结果显示,在车辆设备维护的决策过程中可以使用博弈方法,其结果具有实效性,在维护决策的过程中具有优先权者则具有更大的优势,通过跟传统优化方法进行比较,可以得出博弈方法具有动态性好、灵活性强、适应性好的优势特点,对于管理层的决策工作具有积极影响的研究结论。
关键词:地铁车辆;设备运行;维护;博弈协作
前言
就目前的实际情况而言,想要实现企业利益最大化的重要决策方法就是优化理论,其作为当下关于设备维护决策的热门研究内容,对于企业获得决策目标的静态最优解以及企业利益总体最大化有着积极的作用。然而,这种方法对于企业下属各部门的利益分配问题进行了忽视,使得各部门之间的利益无法得到均衡。
基于这个原因,让博弈理论得到了施展空间。作为实施决策的重要方法,博弈理论可以将具有约束的、多人多目标的函数间的矛盾问题有效解决,被广泛应用于路径规划、供应链以及交通运输等领域。目前,针对于设备管理决策领域的博弈理论,主要是被用于生产调度。文章通过地铁车辆的关键设备进行研究,利用分析结论对博弈方法的有效性和适用性进行了验证。
维护策略的描述与假设
文章围绕地铁车辆的假修修程为研究内容,将运营方和维护方假设为博弈两方,博弈的过程具有有效性。同时,在不影响模型适用性和贴近实际情况这两个条件下,假设模型的设备是刚开始使用的新设备,所采用的维护方法虽然具有预防性质,但存在缺陷,维护的效果属于修复非新。设备出现的故障时可以采用小幅度修复的,经过修复后的状态保持在故障发生前,对故障的衰退速率不造成任何影响。针对设备故障率进行函数计算的是适应能力较强的威布尔分布。假设设备处于载荷状态下的转换,不会让时间和成本减少。设备在进行预维护的操作时间要控制在整车的规定的维修库停时间内。
模型推导
2.1载荷转换建模
因为运行环境和特殊运用规律对车辆造成的影响,会使车辆设备的衰退速率出现时快时慢的现象。其中,载荷对于车辆设备衰退的影响最大,所以,将设备衰退的主要原因设置为载荷,将衰退过程根据载荷状态不同的衰退区间进行划分,让设备在不同的区间内承受多种工作载荷,遵循多种衰退规律。假设设备故障率函数服从三参数威布尔分布,机械载荷作用L和尺度参数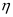 的公式表现为
的公式表现为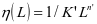 ,相关参数由
,相关参数由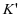 、
、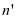 进行表示。基于文中设备载荷作用下衰退情况不同,所以,
进行表示。基于文中设备载荷作用下衰退情况不同,所以,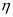 会以不同方式表现设备不同载荷状态L。假设在第j个载荷区间中设备故障率函数
会以不同方式表现设备不同载荷状态L。假设在第j个载荷区间中设备故障率函数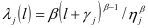 ,可靠度函数的表示是
,可靠度函数的表示是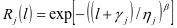 ,假设设备处于载荷状态
,假设设备处于载荷状态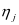 的条件下,继续运行
的条件下,继续运行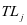 里程后其载荷出现了转换,设备的载荷变换前后的可靠度值数不变,
里程后其载荷出现了转换,设备的载荷变换前后的可靠度值数不变,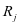
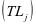 =
=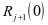 ,由此可得
,由此可得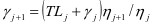 。将预防性维护排除,设备经过了第j次载荷发生变化后故障率函数公式
。将预防性维护排除,设备经过了第j次载荷发生变化后故障率函数公式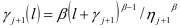 ,其中运行里程的等效为
,其中运行里程的等效为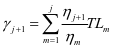 。
。
2.2预防性维护建模
通过非完美维护方法进行维护的设备,其故障率函数的维护前后公式表现为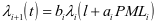 ,
,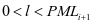 。公式中
。公式中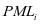 代表第
代表第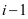 次跟第
次跟第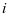 次预防性维护的等效维护间隔;
次预防性维护的等效维护间隔;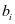 表示的故障率递增因子
表示的故障率递增因子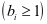 ;
;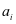 表示役龄递减因子
表示役龄递减因子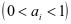 ,在文章中
,在文章中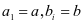 。由此可知,设备经过第
。由此可知,设备经过第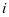 次维护后役龄回退量为
次维护后役龄回退量为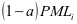 。这里的
。这里的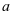 作为维护效果衡量的重要指标,可以从其表现了解设备维护的级别,如果
作为维护效果衡量的重要指标,可以从其表现了解设备维护的级别,如果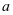 值大,则说明维护级别低,在等效维护间隔
值大,则说明维护级别低,在等效维护间隔 内,存在着多种载荷状态。使用等效转换法可以将不同状态下的运行里程进行统一的等效转换,使其运行里程转变成维护前的状态。
内,存在着多种载荷状态。使用等效转换法可以将不同状态下的运行里程进行统一的等效转换,使其运行里程转变成维护前的状态。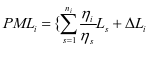 存在载荷转换,
存在载荷转换,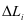 不存在载荷转换。公式经过第
不存在载荷转换。公式经过第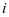 次维护后设备载荷所处状态用
次维护后设备载荷所处状态用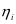 来表示;设备在
来表示;设备在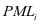 内载荷的转换次数则是由
内载荷的转换次数则是由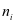 表示;设备在
表示;设备在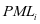 间隔内的第s种载荷状态的运行里程则是由
间隔内的第s种载荷状态的运行里程则是由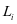 表示;第
表示;第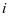 次的预维护时设备处于载荷
次的预维护时设备处于载荷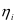 状态下的运行里程数由
状态下的运行里程数由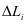 表示。当可靠度下降到了维护阙值R的状态时,想要让设备可以可靠运行,就一定要进行预防性的维护,设备可靠度的公式表现为
表示。当可靠度下降到了维护阙值R的状态时,想要让设备可以可靠运行,就一定要进行预防性的维护,设备可靠度的公式表现为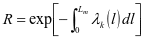 ,其中
,其中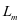 表示的就是故障率函数演化为
表示的就是故障率函数演化为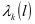 时,设备所需预定运行里程数可以让可靠度下降到R,利用
时,设备所需预定运行里程数可以让可靠度下降到R,利用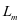 可以将预防性维护的时机进行确认。
可以将预防性维护的时机进行确认。
2.3设备的维护成本
关于预防性维护成本的计算,需要利用J.Pongpech等人进行的构成预防性成本的相关研究得出公式: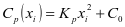 ,其中设备在第
,其中设备在第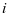 次预防性维护的役龄回退量用
次预防性维护的役龄回退量用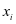 表示,单词预防性维护的基本费用用
表示,单词预防性维护的基本费用用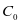 来表示,可变成本率则是由
来表示,可变成本率则是由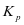 来表示,通常又可以指代为了能够增大单位修复程度而使用的成本。一般设备对于最大故障维修时间
来表示,通常又可以指代为了能够增大单位修复程度而使用的成本。一般设备对于最大故障维修时间
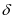 会进行规定,假如故障没有在规定时间内完成排除工作,故障维修就会出现惩罚。文章的条件设定为无记忆性的指数分布,表示维护的经验和故障维修时间没有任何关联,概率密度的计算函数为
会进行规定,假如故障没有在规定时间内完成排除工作,故障维修就会出现惩罚。文章的条件设定为无记忆性的指数分布,表示维护的经验和故障维修时间没有任何关联,概率密度的计算函数为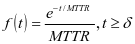 ,公式中的MTTR即平均故障修复时间,当小修复时间超过
,公式中的MTTR即平均故障修复时间,当小修复时间超过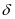 之后,惩罚成本用
之后,惩罚成本用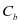 来表示,那么,每次小修的故障成本
来表示,那么,每次小修的故障成本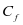 可知是
可知是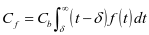 ,其中小修时间超出
,其中小修时间超出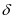 的部分就是
的部分就是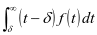 ,单次的小修平均成本就是
,单次的小修平均成本就是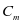 。单次进行维修所产生的附加成本就用
。单次进行维修所产生的附加成本就用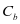 来表示,维护的总体成本的则是
来表示,维护的总体成本的则是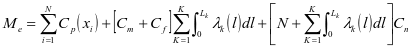 ,其中维护设备的总次数用N表示,有限区间内设备的故障率突变阶段的数值则是用K表示。
,其中维护设备的总次数用N表示,有限区间内设备的故障率突变阶段的数值则是用K表示。
2.4设备的可用度
设备维护的时间和维护周期所使用的统计单位存在差异,因此,利用转换系数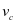 进行维护时间和潜在走行距离的转换,设备的可用度用A来表示,其公式为
进行维护时间和潜在走行距离的转换,设备的可用度用A来表示,其公式为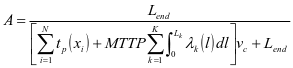 维护的经验、级别、设备状态等因素都会对预防性维护的时间产生影响,所以预维护时间时在设备役龄等效回退量的基础上计算得来。
维护的经验、级别、设备状态等因素都会对预防性维护的时间产生影响,所以预维护时间时在设备役龄等效回退量的基础上计算得来。
建立博弈模型
3.1博弈模型一:假设一运营方作为优先的领导者,运营方先行动进行第二轮的博弈,将预防性维护的博弈初始阙值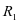 进行了明确,这时,运营方的决定会让维护方进行反应,想要保证维护成本的最小值必须选择最优值
进行了明确,这时,运营方的决定会让维护方进行反应,想要保证维护成本的最小值必须选择最优值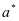 ,公式表示min
,公式表示min 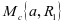 ,让
,让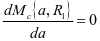 就可知维护方最优反应量
就可知维护方最优反应量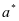 。因为在第一轮的博弈中,运行方已经想到,维护方会由于自身选择
。因为在第一轮的博弈中,运行方已经想到,维护方会由于自身选择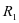 而选择
而选择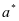 ,为了让可用度达到最大值数,运行方会为了满足维护方的要求而将阙值定为最优值
,为了让可用度达到最大值数,运行方会为了满足维护方的要求而将阙值定为最优值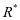 ,所以max
,所以max 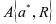 ,让
,让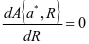 ,运营方的最优反应量
,运营方的最优反应量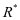 变为可知,模型一的子博弈纳什均衡解为
变为可知,模型一的子博弈纳什均衡解为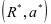 。
。
3.2博弈模型二:以维护方作为优先领导者,维护方就要在第二轮博弈中先开始行动,将维护阙值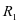 确定,运营方的反应有维护方的决定而得出,最优值选择
确定,运营方的反应有维护方的决定而得出,最优值选择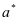 ,可用度的最大数值可以得到保证,公式max
,可用度的最大数值可以得到保证,公式max 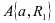 ,使
,使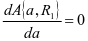 ,运营方的最优反应量值就可计算出。
,运营方的最优反应量值就可计算出。
此时维护方想要得出的模型二的子博弈纳什均衡解是由min 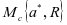 求其中的R,使
求其中的R,使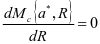 ,维护方最优反应量为
,维护方最优反应量为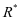 ,结果为
,结果为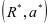 。
。
结论
综上所述,文章以非完美维护策略和博弈理论假设条件,将两类博弈模型的纳什均衡解用逆向归纳法进行求解,其结果是满足于双方要求的维护方案,对维护决策中应用博弈方法的可行性和适用性进行验证。通过博弈的平衡与比较,具有优先权就会对维护决策的影响更大,更具有决策优势。博弈方法的灵活度与适应性都要比传统优化方法要更好,对设备维护计划的决策变得更加灵活,对合理制定维护计划提供了指导意见,对其决策提供了有力证明。
参考文献
[1]向伟彬,王亮.地铁车辆场段工艺设备检修管理影响因素探析[J].中国标准化,2019(22):222-223.
[2]王国平,孟鹤,施江泳,杨晓云,耿烽.地铁车辆底架吊挂设备连接紧固件特性研究[J].电力机车与城轨车辆,2019,42(05):25-28.
[3]郭瑾. 地铁车辆设备管理系统的设计与实现[D].吉林大学,2016.
[4]王红,刘志龙,杜维鑫,蒋祖华.地铁车辆设备运用与维护的博弈协作研究[J].交通运输系统工程与信息,2016,16(05):21-26.