经历过程 悟得算理 归纳算法——以《分数乘整数》为例谈对学生运算能力的培养

经历过程 悟得算理 归纳算法——以《分数乘整数》为例谈对学生运算能力的培养

刘剑

温州市龙湾区横街学校   325000

【摘 要】小学数学计算教学对小学生来说是学习数学的基础,学生的运算能力主要包括简单数字的加、减、乘、除,传统小学数学运算能力的培养是让学生死记硬背计算公式,学生在真正的运用过程中往往不能够直接的去计算,这导致学生的运算速度降低。为了提高学生的运算能力，本文以人民教育出版社“义务教育教科书”小学数学六年级上册第一单元“分数乘整数”的教学内容为例，结合笔者的教学实践，探讨教学过程中出现的一些问题，介绍相应的教学尝试及自我感悟。在教学过程中，探索算法与算理相融合，提高核心素养下学生运算能力的培养。

【关键词】分数 整数 运算

一、教与学概述——直面课堂教学本质

“分数乘整数”人教版六年级上册第一单元的内容。分数与整数相乘是“分数乘法”单元教学的内容，是学生学习分数乘法意义的起点。这部分内容是在学生已学的整数乘法的意义和分数加法计算的基础上进行教学的。通过学习，为进一步学习“分数乘小数”、“分数乘分数”和分数除法、分数四则混合运算，以及解决更多的有关分数的简单实际问题奠定基础。

学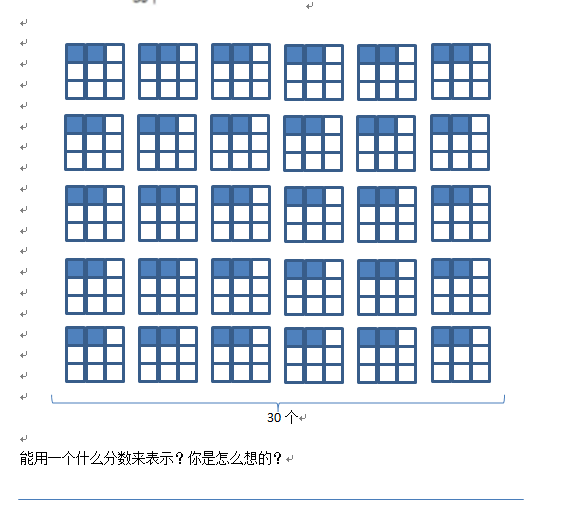 情分析：一直以来，但凡是计算。要么数不过来，要么不好数，才想起来要计算。算的话，可以是加减法，也可以是乘除法，可以是估着算，也可以是按照算理准确计算。学生掌握分数乘整数的关键是：①理解分数乘整数的意义，理解几个几分之几相加，就是几乘几分之几。②掌握乘的计算过程。学生在这之前已经有了乘法的一些计算方法，能够准确计算整数乘法。为了了解学生是怎么联系加法和乘法的，是怎么理解分数乘整数的，分数乘整数的计算方法是怎样的。我在教学实践前，让学生做了导学任务。学生完成后的情况反馈是这样的：

从表中我们发现，学生分数乘整数，分子与整数相乘，分母不变的学生只有9人，占全班的21.95%，分子与分母分别与整数相乘的学生有32人，占全班的79.05%。为什么会有这么大的差别呢？事实上，学生受整数乘法的影响太大了，一股脑全部乘起来。那么做对的同学是不是已经明白了其中的算理呢。经过后来的调查，9个人里也就只有4个人是会算的，要么外面学习学的，要么家长教的，其余的5个是跟着感觉走。

专家解读：“分数乘整数”属于《数学课程标准》（2015年）划分的数学四大学习领域之一“数与代数”， 在“数与代数”的教学中，应帮助学生建立数感和符号意识，发展运算能力，树立模型思想。运算是“数与代数”的重要内容，运算是基于法则进行的，通常运算满足一定的运算律。学习这些内容有助于理解运算律，培养运算能力。“分数乘整数”是该块知识中的一个点。而在常态教学中，有的教师总存在着一些 “操作活动表面化”、“认知体验形式化”、“算法理解孤立化”等教学缺失，导致学生对知识的理解似懂非懂，教学流于肤浅。若这块内容把握不好，对后续的学习造成直接的影响。

二、思考与实践——从理解走向深刻

因为教师轻过程，重结果的教学意识，导致学生“知其然，而不知其所以然”。问题的源头在课堂教学，回归课堂，深思慎教。以下是笔者在教学中由若干问题引发的一些思考与实践，以及触类旁通，寻到的一些耐人寻味的知识共性。

思考1：把算法“分子乘分子，分母不变”说成“分子乘分子，分母乘分母”仅仅是口误吗？

教学中发现学生会把“分子乘分子，分母不变”说成“分子乘分子，分母乘分母”，纠正多次还是改不了，这仅仅是口误? 还是受其他知识影响。深入思考，不难发现，学生受之前学习整数乘整数的计算算法影响，看到数字之后两两相乘，这样一来思维定势，无法将数理应用于计算中去。而分数乘整数对于学生来说是刚刚接触的，还没有真正清晰分数乘整数的算理表象，产生“口误”。

【对策】 “法”、“理”相融，提高运算能力

小学生的思维以形象思维为主，逐步向抽象思维过渡。表象是由感知觉到概念间的“阶梯”，具有直觉性和概括性。笔者认为我们应该以直观形象的教学手段为基点，沟通分数的意义、加法的意义、乘法的意义间的联系，通过多个教学环节丰富学生的感知、理解，帮助学生建立清晰的、深刻的表象，训练学生的运算能力，让学生的核心素养得到更好的发展。

（1）关注加法向乘法过渡，深刻经历过程

运 算算理表象的形成需要经历一个不断提高、延伸、完善的学习过程。而乘法的运算，教师不仅要注重学生对数的观察研究，还要关注数从加法到乘法的过渡，体会加法与乘法的联系，理清它的纵向发展脉络。如教学“分数乘整数”课始，笔者利用多媒体设计了一个情境导人新课。屏幕先出现一个正方形，提问：你会想到哪个数，紧接着把正方形平均分成9份，其中2份图上颜色，提问：现在又会想到哪个数，最后屏幕上出现了30个这样的正方形，问：现在呢？

随着“1→ →30个 相加→ 30× ”的过渡 ，让学生不断观察、思考，感受分数、整数、分数的意义、加法的意义和乘法意义的联系与区别，巧妙地实现了加法向乘法的过渡，帮助学生实现了从抽象到具体的转化。一个精心设计的小环节让学生印象深刻，就不会轻易地将算理说错了。

（2）重视乘法运算的建构，真正悟得算理

分数乘整数是这个单元的起始课，也是对后面学习分数乘分数，分数乘小数的关键。因此对这个知识点的建构尤显重要。在乘法意义的教学过程中，教师应充分让学生借助图来理解分数乘整数的实际意义，进而理解算理。如教学用乘法表示30个 时，首先让学生明白，可以用加法算式来表示，也可以用乘法算式来表示。再让学生明确乘法算式中，各部分所表示的意思，最后揭示课题。

（3）降低乘法运算的难度 ，归纳计算方法

学 生的运算能力不同，导致学生运算的速度、准确度也各不相同。显然复杂的计算会影响一些学生的理解和掌握。如在教学30× ，学生在计算时，数据过大，一些学生不能够结合原有的加法算法表象来计算，一些学生甚至因为数据的过大，开始担心、害怕。为了避免优等生“吃不饱”，后进生“吃不好”，笔者把研究对象改为4× ，这样一来，化繁为简，优等生可以在建立分数乘整数的算理表象的同时，去思考更为复杂的算式，而后进生则可以通过加法算理去理解掌握分数乘整数的乘法算理。

思考2：在教学前，要做前测吗？

在平时的教学过程中，笔者发现在教学计算课时，学生们往往会在课中的时候会算，课后反而会算错。这个过程反应了学生在课堂中算理的掌握有一定的问题，除此之外，很多时候在计算的过程中会暴露一些问题，而这些问题，有的时候同桌之间的交流，或者同学之间的交流会得到解答，碍于面子，一些学生会选择我已经理解了，而这些理解又是表面化的。真正暴露问题，为不能解决的时候确是在课后。

【对策】 在暴露问题中，提高运算能力。

运算能力的培养需要通过不断的分析，比较，归纳为基础，当学生通过大量的错题分析，尤其是错误点的暴露，这样一来，大家都会清楚哪些地方是会容易出错的，会出什么样的错误。这样，学生在不断分析，比较，归纳的过程中，加深对分数乘整数算理的理解，培养运算能力。

（1）暴露问题

笔 者在教学之前做了30× 怎样计算，把计算过程写完整这样的课前测试，测试结果反映如下：参加测试的学生：41人。计算时按“分子与分子相乘，分母与分母相乘”的有32人，占全班总人数的79.05%；计算时按“分子与分子相乘，分母不变”的有9人，占全班总人数的20.95%。

两个算式都是孩子们认为计算的方法，计算的结果却不一样。这样一来引起学生的质疑，勾起学生研究的兴趣。

（2）分析问题

事实上，学生受整数乘法的影响太大了，一股脑全部乘起来。那么做对的同学是不是已经明白了其中的算理呢。经过后来的调查，10个人里也就只有4个人是会算的，要么外面学习学的，要么家长教的，其余的6个是感觉这么做。

（3）解决问题

这 个时候，暴露的问题急需要做解答，在这个教学环节中，笔者还学于生，让学生自主探索问题的关键所在。在计算过程中，整数30太大了，不便于研究，我们先来研究4× ，从中找出计算的方法。学生通过学习任务单的学习，写出或画出了自己思考的计算过程，帮助学生理解30× 算理，掌握算法。

学习任务:用自己的办法写出或画出30× 的计算过程，完成之后可以同桌先交流。

学生的运算能力是在训练过程中逐步建立、形成、强化和发展起来，非一朝一夕之事，切勿操之过急，只要教师在教学过程中始终已贯彻明晰算理，强化提升，算理与算法相融，这样一来学生学习算理会由模糊走向清晰，学生的运算能力也会由弱到强，由单一到复杂地不断提升。

【参考文献】

1．义务教育教科书《数学》六年级上册.人民教育出版社

2．义务教育教科书《数学》教师用书四年级上册.人民教育出版社

3．马云鹏.《小学数学教学论》.人民教育出版社

6