浅析“锥形视线法”在工程测量中的应用

浅析“锥形视线法”在工程测量中的应用

李星文

柳州市建筑工程集团有限责任公司 广西柳州 545000

摘要：在市政道路、管道工程、小区配套工程建设等施工过程中，利用水准仪的水平视线法测设坡度线相比倾斜视线法，工效低而且发生失误的概率高，运用倾斜视线法有着很好的应用价值，“锥形视线法”是在倾斜视线法的基础上，笔者通过实践及翻阅大量理论资料总结而来，在工程测量过程中应用方便快捷，减少失误，极大的提高工作效率。

关键词：坡度测设；倾斜视线法；锥形视线法；精度分析

直线坡度 i 是指两端点的高差与两点的水平距离之比，即 i=h/D，常以百分率表示。在工程测量的教学实习中翻阅大中专院校工程测量教材、期刊论文及实践过程中对已知坡度线的放样方法总结出锥形视线法的运用，本文以具体实例及数据表格进行分析。

一、利用微倾水准仪进行坡度线测设

某小区室外配套工程建设：修筑 AB 段 150m 的小区道路，如图 2；起点路床面标高为106.00，按 8%的坡度修筑，道路宽为 6m。以上述为例简单叙述倾斜视线法的原理：分别在A 点、B 点打一个标记桩，然后通过水准点测量这两个标记桩顶标高，A 点桩顶标高为106.25， B 点的桩顶标高为 94.50；然后重新架设仪器至 A 点上，架设仪器时，用线坠等工具对中， 然后仪器三个脚螺旋尽可能的其中两个与所测设的坡度线垂直，并且第三个脚螺旋按一个方向尽可能的拧到头，此时用脚架粗略调平水准仪，然后精平。用卷尺量取水准仪十字丝中心线位置至桩顶的高度为 1.25m，确定修筑路床坡度线的水准尺读数为 1.25+0.25=1.5m。如图 1。完成上述步骤，接下来就要用第三个脚螺旋来调至 8%的坡度，在 B 点立好水准尺，调整第三个脚螺旋直至看到读数 1.5-{94.5-（106-150*8%）}=1m 即完成坡度线的设定；此时在修筑路床的过程中， 在 AB 连线上即看读数 1.5m 即可；与水平视线法相比，不用移站，不需要量取距离和过程计算，避免了量距和计算错误带来的失误，此种测量方法只是应用在AB这条中心线上，对于实际道路施工应用方面受到限制。笔者在此基础上分析了利用经纬仪或者全站仪转动过程形成的轨迹进行了误差分析，在精度要求不高，尤其是基层土方施工过程利用经纬仪或全站仪进行测量，失误小，效率高。

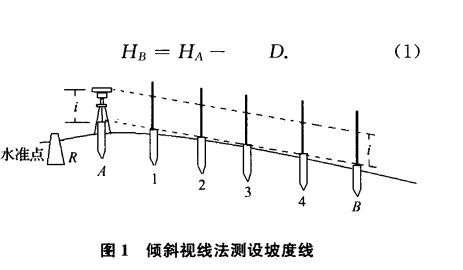
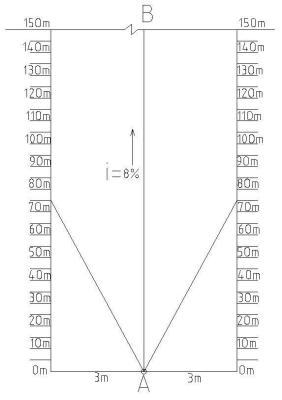
图 2

二、利用经纬仪或全站仪测设坡度线。通过三角高程测量，观测两个控制点的水平距离和天顶距(或高度角)求两点间高差。通俗来讲，测设坡度线是用三角高程测量替代水准测量。如图3，A、B为地面上两个控制点，自A点观测B点的竖直角为α，D为两点间水平距离，i为A点仪器高，v为B点觇标高，则A、B两点间高差为:hAB=Dtgα+i-v （1）

上式必须假设地球表面为一平面，观测视线为直线才成立。在大地测量中，当两点距离大于300m时，应考虑地球曲率和大气折光对高差的影响。 三角高程测量，一般应进行往返观测(双向观测)，它可消除地球曲率和大气折光的影响。在住宅小区道路、管线施工等工作中，土方开挖等工序相对来说精度要求不是特别高，在距离不远的情况下，应用全站仪任意架设在未知的便于观测的高程点HA（本文以修路为例，仪器架设在道路中心线或反向延长线）上，通过已知高程点HB反算得到HA的高程，进而测量其他未知点的高程或坡度线。

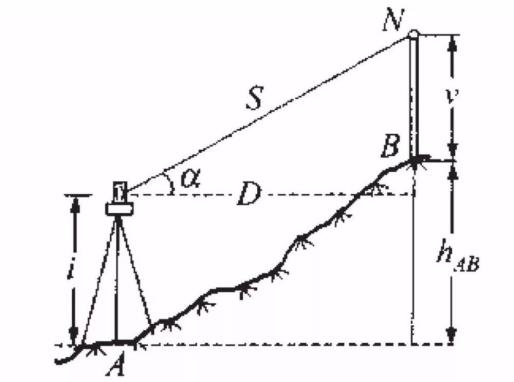
图3

首先由(1)式可知:

　　HA=HB-(Dtanа+i-v) (2)

　　上式除了Dtanа即Z的值可以用仪器直接测出外,i,V都是未知的。但有一点可以确定即仪器一旦置好,i值也将随之不变,同时选取跟踪杆作为反射棱镜,假定V值也固定不变。从(2)可知:

　　HA+i-V=HB-Dtanа=W(3)

　　由(3)可知,基于上面的假设,HA+i-V在任一测站上也是固定不变的.而且可以计算出它的值W。通过后视已知高程点HB，能计算W值，全站仪测量过程，水平距离D，及高度角均可知。量取仪高i（或者为零，反算HA时就为仪器照准部十字中心线处的高程），设定棱镜高V。仪器任一置点,但所选点位要求能和已知高程点通视。

用仪器照准已知高程点,设定棱镜高V的值,并算出W的值。(此时与仪器高程测定有关的常数如测站点高程,仪器高,棱镜高均为任一值。施测前不必设定。)

把W当做架设仪器位置的点的高程来用，仪器高和棱镜高设为0即可。　照准待测点测出其高程。结合(1),(3)

　　HB′=W+D′tanа′ (4)

　　HB′为待测点的高程

　　W为测站中设定的测站点高程

　　D′为测站点到待测点的水平距离

　　а′为测站点到待测点的观测垂直角

　　从(4)可知,不同待测点的高程随着测站点到其的水平距离或观测垂直角的变化而改变。

　　将(3)代入(4)可知:

　　HB′=HA+i-v+D′tanа′(5)

　　按三角高程测量原理可知

　　HB′=W+D′tanа′+i′-v′ (6)

　　将(3)代入(6)可知:

　　HB′=HA+i-t+D′tanа′+i′-t′ (7)

　　这里i′,t′为0,所以

　HB′=HA+i-t+D′tanа′ (8)

　　由(5),(8)可知,两种方法测出的待测点高程在理论上是一致的。此方法进行三角高程测量是正确的。

上述推导过程即完成了实际测量过程，任意将仪器置于未知高程点上进行坡度线测设的理论依据。现行的多种全站仪均有上述反算功能，如尼康2.0M中的“后视BM”功能。通过此功能可以快捷的知道未知点的高程，通过仪器面板显示的坡度或角度来进行坡度线测设。

三、经纬仪或全站仪的“锥形视线”

经纬仪旋转照准部时，本身的基座没有倾斜，而是照准部围绕着竖轴转动，视线形成的轨迹是一个圆锥面，用一个竖平面去切不经过中心的圆锥体的时候，相交形成的图形是双曲线的一支，如图 6；本方法不需要研究双曲线的焦点、焦半径等问题；只需分析被一个竖直平面所切的锥面上的点至这个圆锥顶的垂直距离；如图 5：

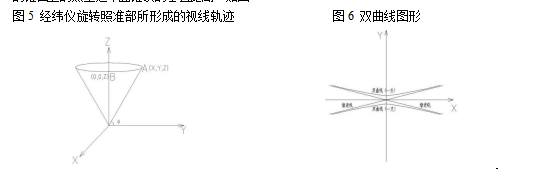
当测量道路左边桩中桩右边桩时，即变成研究被一个竖直平面去切圆锥视线轨迹的问题，由此分析可得 tanθ=OB/AB=|Z|/√(X^2+Y^2)；所以锥面方程：Z^2=(tanθ)^2(X^2+Y^2), 由下列数据表 2 分析：

从上述表格得知坡度越小、路幅越窄、距仪器越远，测量点左右边点距中点的偏差就越 小；在某些施工工序（土方开挖）不需要特别精确的的测量结果时，可以利用上述结论把“锥形视线测设”当做是坡度线测设。实际操作过程，我们可将仪器架设在起始点后退一段距离的位置上，以减小误差。既方便施工，提高了效率，又可避免计算错误等大的失误。

由此可知“锥形视线法”在工程测量中高效便捷，而且还能在一些成形的道路改造或翻修过程中，通过测量能很快的提供数据便于决策。

参考文献：

【1】阚柯 建筑工程测量与施工放线一本通 【M】北京：中国建筑工业出版社，2009：236~238

【2】邱万作 直说圆锥曲线 【M】上海：上海科学技术出版社，2012：92~94