陕西省城固县城固第一中学 723200
解决双变量“存在性或任意性”问题关键就是将含有全称量词和存在量词的条件“等价转化”为两个函数值域之间的关系(或两个函数最值之间的关系),目的在于培养学生的逻辑推理素养和良好的数学思维品质.笔者在教学实践中发现这类问题具有以下几种类型,现小结如下和大家交流。
类型A 形如“对任意x1∈A,都存在x2∈B,使得g(x2)=f(x1)成立”
1. 已知函数f(x)=x3+(1-a)x2-a(a+2)x,g(x)=x-,若对任意x1∈
[-1,1],总存在x2∈[0,2],使得f′(x1)+2ax1=g(x2)成立,求实数a的取值范围.
解 由题意知,g(x)在[0,2]上是一次函数并且单调递增故它的值域为.
构造新函数h(x),令h(x)=f′(x)+2ax=3x2+2x-a(a+2),对h(x)求导并求出它的单调区间和值域,则h′(x)=6x+2。令h′(x)=0得x=-,-将[-1,1]分为两个区间 和 。当x∈时,h′(x)<0 , h(x)为单调递减函数;当x ∈ 时,h′(x)>0,h(x)为单调递增函数。所以[h(x)]min=h =-a2-2a-,[h(x)]max=h(1)或h(-1)
又由题意对“任意x1∈[-1,1],总存在x2∈[0,2],使得f′(x1)+2ax1=g (x2)成立”所以h(x)的值域是函数g(x)的值域 的子集,所以
解得实数a的取值范围是[-2,0].
小结 理解全称量词与存在量词的含义是求解本题的关键,此类问题求解的策略是“等价转化”,即“函数f(x)的值域是g(x)的值域的子集”从而利用包含关系构建关于a的不等式组,求得参数的取值范围.
类型B 形如“存在x1∈A及x2∈B,使得f(x1)=g(x2)成立”
2. 已知函数f(x)=函数g(x)=ksin-2k+2(k>0),若存在x1∈[0,1]及x2∈[0,1],使得f (x1)=g (x2)成立,求实数k的取值范围.
解 由题意当x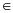 时,通过直接求导可知 f′(x)=
时,通过直接求导可知 f′(x)=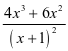 显然f′(x)>0, 可判断函数f(x)在区间 上是单调递增函数,所以f(x)的值域为[
显然f′(x)>0, 可判断函数f(x)在区间 上是单调递增函数,所以f(x)的值域为[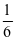 , 1];当x
, 1];当x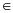 [0,
[0,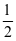 ]时,f(x)=
]时,f(x)=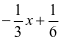 显然是单调递减函数,所以它的值域为[ 0 ,
显然是单调递减函数,所以它的值域为[ 0 , 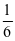 ]. 由上可知f(x)的值域为[0,1].对于函数g(x),由于k>0,x2∈[0,1]则g(x)也是增函数,故它的值域为。由题意 ”存在x1∈[0,1]及x2∈[0,1],使得f(x1)=g(x2)成立”所以两个函数的值域有公共部分。直接依据这两个区间有“公共部分”列不等式情况较复杂,如果利用“补集思想”则比较容易。先求它们没有公共部分的情况,即2-2k>1或2-k<0,解得k<或k>,要使两个函数值域有公共部分,k的取值范围应该是k<或k>在实数集R上的补集.
]. 由上可知f(x)的值域为[0,1].对于函数g(x),由于k>0,x2∈[0,1]则g(x)也是增函数,故它的值域为。由题意 ”存在x1∈[0,1]及x2∈[0,1],使得f(x1)=g(x2)成立”所以两个函数的值域有公共部分。直接依据这两个区间有“公共部分”列不等式情况较复杂,如果利用“补集思想”则比较容易。先求它们没有公共部分的情况,即2-2k>1或2-k<0,解得k<或k>,要使两个函数值域有公共部分,k的取值范围应该是k<或k>在实数集R上的补集.
小结 本类问题的实质是“两函数f(x)与g(x)的值域的交集不为空集”,上述解法的关键是利用了补集思想.
变形:若把此种类型中的两个“存在”均改为“任意”,则“等价转化”策略是利用“f(x)的值域和g(x)的值域相等”来求解参数的取值范围,这个变形读者可以尝试自行解决。
类型C 形如“对任意x1∈A,都存在x2∈B,使得f(x1)<g(x2)成立”
3. 已知函数f (x)=x+,g (x)=2x+a,若任意x1∈,存在x2∈[2,3],使得f(x1)≤g(x2),则实数a的取值范围是________.
解析 依题意知[f (x)]max≤ [g (x)]max.
∵f(x)=x+ 在 上是减函数,
∴f(x)max=f =.
又g(x)=2x+a在[2,3]上是增函数,∴g(x)max=8+a,
因此≤8+a,则a≥.
答案
小结 理解量词的含义,将原不等式转化为[f(x)]max≤[g(x)]max;利用函数的单调性,求f(x)与g(x)的最大值,得关于a的不等式求得a的取值范围.
思考1:在3.中,若将“任意x1∈”改为“存在x1∈”,其它条件不变,则a的取值范围是______.
问题“等价转化”为[f(x)]min≤[g(x)]max,可仿照3 解答.
将3.中的逻辑连接词“任意”改为“存在”即:
已知函数f(x)=x+,g(x)=2x+a,若存在x1∈ ,存在x2∈[2,3],使得f(x1)≤g(x2),则实数a的取值范围是________.
解析 : 依题意可知[f(x)]min≤[g(x)]max
∵f(x)=x+在上是减函数,
∴f(x)min=f(1)=5
又g(x)=2x+a在[2,3]上是增函数,∴
g(x)max=8+a,
因此5 ≤ 8+a , 则a 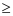 3 .
3 .
思考2:在3.中,若把“存在x2∈[2,3]”变为“任意x2∈[2,3]”时,其它条件不变,则a的取值范围是________.
问题“等价转化”为[f(x)]max≤[g(x)]min,可仿照3解答.
将3.中的逻辑连接词“存在”改为“任意”即:
已知函数f(x)=x+, g(x)=2x+a,若任意x1∈,任意x2∈[2,3],使得 f (x1)≤g (x2),则实数a的取值范围是________.
解析 依题意可知[f (x)]max≤[g(x)]min,
∵f(x)=x+在上是减函数,
∴f(x)max=f =
又g(x)=2x+a在[2,3]上是增函数,∴g(x)min=4+a,
因此 ≤ 4 + a ,则 a 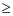
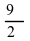
上述两种变化关键在于深刻理解:将逻辑联结词变为“任意”和“存在”后最大值和最小值关系的变化!
以上三种类型中类型A和类型B结合逻辑联接词“存在”和“任意”意义分别转化为集合之间包含关系给予解决;类型C对逻辑联接词理解应用要求更高,除正确理解逻辑联接词意义外还必须应用两个函数最大值与最小值之间关系列不等式求参数范围,应多思考多训练达到熟能生巧。掌握以上几种类型并灵活应用,在以后学习中涉及到“双变量问题”一定会迎刃而解。
2020年7月5日