反问题与神经网络相结合的混流泵叶片优化设计

反问题与神经网络相结合的混流泵叶片优化设计

董宏平

国投新疆罗布泊钾盐有限责任公司 新疆哈密市 839000

摘要：针对三元扭曲叶片优化设计过程中设计变量较多的问题，采用动量矩为设计变量，再通过反问题计算得到叶片来间接对叶片进行参数化；针对评价函数计算量太大的问题，根据试验设计理论安排训练样本，采用神经网络建立设计变量与目标函数间的复杂的响应关系，并且详细研究了反向传播和径向基函数2种网络在对评价函数进行预测过程中的应用，建立了一种新的叶片优化设计方法.与传统的优化方法相比，其设计变量数目较少，以叶轮内的三维粘性流动分析为基础且大大缩短了计算时间.利用此方法对一台混流泵的扬程和效率进行优化，所得叶片性能良好，从而验证了此方法的有效性.

关键词：反问题；神经网络；优化

流体机械叶轮叶片的设计通常采用2种方法:反问题计算和优化设计.反问题计算即给定叶片表面的速度、压力或者动量矩等的分布计算求出相应的叶片几何形状，需要设计者具有丰富的设计经验.对于该方法的研究，文献进行了详细的总结，此处不再赘述.优化方法是工程设计的发展方向，但目前在流体机械领域的研究大多集中在二维翼型方面，对三元扭曲叶片优化的研究较少.作者认为原因之一就是对三元扭曲叶片的几何形状进行参数化描述所需的参数较多而导致优化设计操作困难.

1计算方法

1.1反问题计算

本文采用圆柱坐标系描述叶片的几何形状，即:

.首先，根据给定的设计参数进行方案设计来确定叶轮子午流道的形状，在子午流道中建立流线-准正交线(m-q)坐标.然后，求解速度梯度方程及质量守恒方程得到叶轮流道内的相对速度

(1)

Wr，再根据式(3)计算叶片的角坐标就可得到三元

EL (/rW1%dm+d7V

扭曲叶片的几何形状.具体的计算方法见文献[6],此处仅给出主要的计算公式如下：

沿准正交线方向的速度梯度方程为

IWrdq(2)

质量守恒方程为

Q=p(#r—t0N')cos(a—$)Wmdq (2)

叶片的角坐标为

式中：A、B、C为系数；m为子午流线的相对长度；Q为流量:

此处采用动量矩作为叶片的控制参数，其突出优点是将沿流线流体微团的与叶轮的理论功直接联系起来，并且VG沿流线的变化率与叶片的载荷紧密相关，通过对FG的控制可以控制叶片载荷的分布.VG在子午流道内的分布为一个空间曲面，严格地讲应该将所有计算节点的VG均作为设计变量进行优化，实际上这是难以实现的.为减少设计变量，设计中规定轮盘和轮盖处的V°G分布均服从4次多项式规律，即

(,VG)m=am4+bm3+cm"2+dm+e(4)

式中.：、b、c、d、e为系数.一般假定叶片进口处VG为0,出口处由设计参数确定.另外，再给定3个条件即叶片进、出口处d(VG)/dm及m=0.5处V!G的值后，就可以根据上式确定VG的分布.一般假定轮盘与轮盖之间的各流线的V!G服从线性分布规律，这样就可以通过反问题设计计算得到相应的叶片.调整上述6个变量(轮盘、轮盖各3个)的值就可确定不同轮盘轮盖处的V!G分布形式，也就得到了不同形状的叶片.根据经验，本文规定这6个变量的取值范围如表1所示.

表1		设计变量及其取值范围
变量	下限	上限	变量说明
k~0,S	0.0	1:0	轮盖进口处d(VG)/dm的值
71,s	0.0	1:0	轮盖出口处d(V!R)/dm的值
	0:0	1.2	轮盘进口处d(VG)/dm的值
71,H	0:0	1.2	轮盘出口处d(V!R)/dm的值
JH	0:3	0.6	轮盘处m=0.5时VG的值
JS	0.4	0.7	轮盖处m=0.5时VG的值

1.2三维粘性流动分析

对应用本文1.1节所述的设计方法得到的叶轮，再采用计算流体动力学(CFD)软件Fluent对其流道内的三维粘性流动进行数值分析.计算区域及网格剖分如图1所示，对叶轮的进、出口处分别进行延伸，采用六面体非结构化网格剖分计算区域.给定进口的流速，认为出口处的流动是充分发展的，除压力之外的其他变量正法向梯度为0,采用标准—湍流模型.SIMPLE方法进行求解.根据流动分析的结果就可以计算出叶轮的水力效率和扬程.为考察计算单元数对计算结果的影响，对某叶轮分别采用了4种不同的计算单元数进行了分析，图2为叶轮的扬程和效率与计算单元数的关系.可见，当计算单元数从400 000减少到120 000时，扬程和效率的相对变化量分别为0.2%和0.3%,变化较小，但所需的计算时间却大大减少.因此，为减少计算量，本文采用140 000计算单元进行分析.

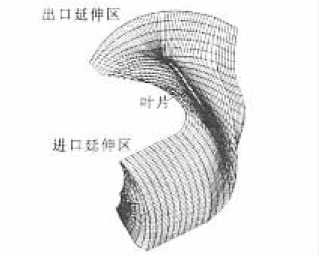
图1计算区域网格剖分示意图

8.4•

冬8.3•

8.2 L

88.0「._

S 87.6-f' 1

87.2 I I > 1

100 200 300 400 500

io_3x计算单元数

图2叶轮性能和计算单元数关系图

1.3优化方法

(/ %			误差/%		H/m			误差/%
CFD	BP	RBF	BP	RBF	CFD	BP	RBF	BP	RBF
87. 106	86.905	87. 012	0 231	0 108	79721	79817	79743	0120	0027
86. 701	86 206	86.929	0 571	0 336	78976	79091	79164	0146	0238
87. 466	87. 240	87. 028	0 258	0 501	79654	79327	79927	0411	0343
87. 222	87. 656	87. 068	0 497	0 211	82212	82189	81898	0028	0382

表2神经网络预测与CFD分析结果的比较

对于不同的问题应根据其具体的特点选择相应的最优化方法.文献分别采用传统的基于梯度类的优化方法及模拟退火算法和遗传算法对混流泵叶片进行了优化，发现叶片的优化问题为多峰值问题，梯度类方法易于陷入局部极小而使得最终优化结果受初始条件的影响很大，即不一定得到全局最优解，而模拟退火算法及遗传算法均能够得到全局最优解.这表明对于三元叶片优化问题，梯度类方法较难胜任，采用演化算法能得到更好的结果，其中遗传算法的鲁棒性较好.遗传算法为仿生类优化方法，具有不受搜索空间限制性条件(如可微、连续、单峰等)的约束及不需要其他辅助信息(如导数)等优点，从而使算法的效率高、宜于操作和通用性好，因此本文应用遗传算法来对叶片进行优化.

优化变量为表1中动量矩分布形式的控制变量.优化目标是叶轮的扬程（H）和效率（（），为多目标优化问题.本文构造一个新的目标函数如下

式中和O分别为单目标优化的最高效率和扬程.这样就将寻找最高H和（的多目标问题转化为寻找最大y值的单目标问题.

对于遗传算法优化过程中的适应函数，即每种动量矩分布所对应叶轮的扬程、效率或丫,在本文中使用1.3节所述的前向神经网络来构造

2计算结果

本文应用上述方法对一台比转速为360的工业用混流泵叶片进行了优化，该泵的基本参数：流量为784 m3/h；扬程为7.73 m；转速为980 r/min.

经CFD分析，该叶轮的效率为86.64%，扬程为7.94 m.首先，应用遗传算法单独对扬程和效率进行优化：采用二进制编码方法，设初始种群大小均为50个，经过100代后最优适应值基本上不再变化，最佳个体的适应值分别为（=88.509%和H'=8.755 m.然后，再对式（5）中的丫进行优化.对扬程、效率进行单目标和多目标优化，所得到的叶片形状分别以Bo表示，其动量矩的分布如图4所示

图5为原始叶片和多目标优化结果的比较图，与原始叶片相比，优化所得的叶片在进口及靠近轮盘处的值变小，在轮盖处的变化幅度较大.

对以上的优化结果进行CFD分析，表3给出了相应CFD分析的叶轮扬程和效率.可见，用本文所

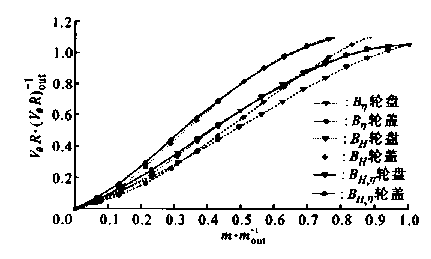
图4优化结果动量矩的分布图

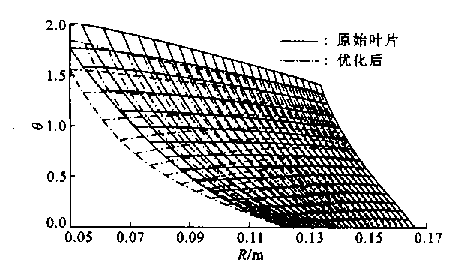
图5原始叶片与优化结果的比较

述的方法优化后叶轮的最咼扬程提咼了0.815 m,最高效率提高了1.869%,多目标优化结果的扬程和效率均较原叶轮有所提高.

表3优化叶片的CFD分析结果

	Bh	B（	Bh
H/m	8.755	8.217	8 222
(/%	87.640	88509	88270

图6为多目标优化结果Bo（所对应叶轮的性能曲线，可见本文所设计的叶轮在非设计工况下性能也较好.

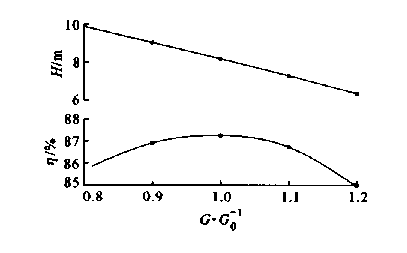
图6叶轮的性能曲线

3结论

本文建立了一种基于三维粘性流动分析的扭曲叶片优化设计方法，以动量矩v成为设计变量间接地对叶片几何形状进行参数化，使得设计变量个数较少.利用神经网络来预测评价函数大大缩短了计算时间.该方法不需太多的设计经验，便于实施.对一台混流泵进行优化，得到了性能良好的叶片，从而验证了该方法的实用性和简便性.

利用均匀试验设计的方法安排训练样本，通过反问题计算和CFD分析得到样本的输出，训练完成的BP网络和RBF网络均能较好地拟合设计变量和目标函数之间的响应关系，其中RBF网络具有更高的精度.

参考文献

[1]曾志波;丁恩宝;唐登海;;基于BP人工神经网络和遗传算法的船舶螺旋桨优化设计[J];船舶力学;2010年Z1期

[2]蔡佑林;王立祥;张新;;喷水推进混流泵叶轮三元可控速度矩设计[J];船舶;2006年01期

[3]史千;刘胜柱;陈元林;;混流式水轮机转轮非设计工况特性分析[J];大电机技术;2008年01期