云南省楚雄市吕合镇中心小学 675009
精心设计练习题是减轻学生负担,培养学生能力,大面积提高教学质量的重要措施之一,就此问题谈一些想法。
一、根椐所学知识的内在联系来设计练习,培养学生探究新知识的能力。
数学学科特点之一是逻辑的严密性,知识之间的内在联系非常紧密。因此,在设计导入新课的练习题时,要充分地利用学生已掌握的旧知识来“穿针引线”,引导他们自己去解决新问题。如:在讲解小数除以小数之前,设计了一组小数除以整数的题目进行新课前复习。
①15.36÷48,②3.22÷14,③10.44÷725。练习后提问学生:
(1)这三道题属于除法的哪种类型?
(2)谁能说出小数除以整数的计算方法?
接着,教师把上面的三道题改为:①15.36÷4.8, ②3.22÷0.14,③10.44÷ 0.725,从而导入新课,接着提出问题:谁能根据“商不变的性质”,把这三道题转化成一个数(整数或者小数)除以整数?让学生自己试算,自己掌握一个数除以小数的计算法则。在此过程中学生自己探究了新知识,教师只是起了点拨引路的作用。
二、根椐学生理解新知识的过程来设计练习,逐步培养学生抽象和概括、分析和综合的能力。
根据小学生的思维特点,我们在进行数学教学时,一般是先让学生观察具体形象的事物,引导他们思考分析,抽取出这-类事物的本质属性,然后把这类属性联结起来,概括为概念。例如帮助学生建立分数概念时,我们总是先让他们观察实物、图片、线段图等,然后
归纳出分数的意义。这时分数意义的教学任务并没有完结,还应当把分数意义的结语这些外在的东西,通过分析、综合转化为儿童内在的认识,使他们把抽象的概念和形象的实例结合起来,概念具体化,而不是生吞话剥地背诵分数意义的结语。为了突出分数与整体“1”
的关系,真正理解分数的意义,可设计如下的练习:
 用一块正方形纸片,怎样折可以得到它的
用一块正方形纸片,怎样折可以得到它的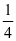 ,有几种折法?学生得出: ......
,有几种折法?学生得出: ......
老师追问:这些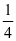 形状不同,大小相等吗?为什么?
形状不同,大小相等吗?为什么?
2、用一张长方体纸片,按照上面的方法折纸,得到的每份都是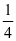 吗? 为什么?
吗? 为什么?

通过观察,对于长方形的第四种折法,每份是不是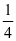 ,可能有两种不同意见。因为分成了两组不同形状的三角形,这四个三角形的面积是否相等呢?有的学生可能产生疑问。在学生不知其解时,教师可
,可能有两种不同意见。因为分成了两组不同形状的三角形,这四个三角形的面积是否相等呢?有的学生可能产生疑问。在学生不知其解时,教师可

以把这个长方形折成下面的样子:学生就能很明显地看出把这个长方形折成八个面积相等的三角形,而第四种折法的每个小三角形都是由上面两个小三角形组成的。因此,第四种折法的四个三角形的面积是相等的(等积不等形)每份也是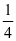 。
。
3.下面的分数表示什么意思。
全校的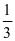 全班的
全班的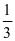 全组的
全组的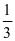
以上“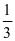 ”所表示的人数相等吗?为什么?
”所表示的人数相等吗?为什么?
三、很据学生运用知识的过程来设计练习,培养学生分析问题和解决问题的能力。
练习题的设计应有阶梯性:由简单到复杂,由一般到特殊,由基本到灵活。般有以下几种:
1.基本练习。运用刚学的定义、定律、法则、性质去解决一个具体问题。这类练习一般是模仿性的,即使这样,也要根据目的任务进行精选。如学习异分母分数加减法,根据通分、约分、把假分数化成带分数或整数等不同情况,加以分析,并由易到难进行安排。大致有如下情况:
①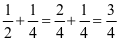
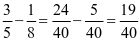
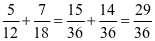 ......
......
②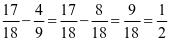 ......
......
③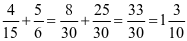 ......
......
第①组三道题代表通分时的三种不同情况,但在计算过程中都不需要约分或化成带分数和整数的,第②组题在计算过程中要约分,第③组题在把假分数化成带分数或整数的。这些题目有明确的目的性,并由浅入深地安排。如果对上述情况不加分析,随意出几道题,题量虽然较多,但效果不见得好。
 2、变式练习。“变式”即变换同类事物的非本质属性, 以便突出其本质特征。通过变式,就能把本质和非本质特征区别开来,加深对概念的理解。如果变式不充分,就会产生缩小概念或不合理的扩大概念的错误。如在讲“垂线”概念时,教师不仅要让学生认识标准图形,即认识两条线成“⊥”这样位置时互相垂直,还应改变方位,出示变式图形,如:
2、变式练习。“变式”即变换同类事物的非本质属性, 以便突出其本质特征。通过变式,就能把本质和非本质特征区别开来,加深对概念的理解。如果变式不充分,就会产生缩小概念或不合理的扩大概念的错误。如在讲“垂线”概念时,教师不仅要让学生认识标准图形,即认识两条线成“⊥”这样位置时互相垂直,还应改变方位,出示变式图形,如:
使学生认识到只要两条直线相交成直角时,这两条线就叫做互相垂直。
又如“差”的概念,学生不仅要知道“男生比女生多3人,女生比男生少3人”,“3”是男、女生人数的差。随着数学知识和生活经验的不断丰富,还应从下列条件中,正确地找出男、女生人数的差。“3名男生到操场打球,剩下的男生和女生同样多。”;“转来3名女生后,男、女生人数同样多。”;男、女生各10人去参加劳动,剩下的男生比女生多3人。”
在教学实践中,我由于能注重课堂上练习的设计,较好调动了各层次学生的积极性,学生的自学能力,智力水平均有不同程度的提高,并使学生对学习数学产生了浓厚的兴趣,同学们都从以前怕上数学课,到现在盼上数学课,初步形成会学、乐学,争先进的良好学风,从而较好地提高了教学效率。