二次根式的复习

二次根式的复习

赵敏华

广东省汕头市东厦中学 515041

（一）教学目标

知识与技能:

1.回忆所学二次根式的基础知识，进一步理解掌握

2. 灵活运用基础知识解决相关问题，提高学生解决问题的

过程与方法 ：

1.学生自查遗忘的知识点，回答问题，提出问题。

2. 经历例题习题的解答，提高技能。

3.讨论、交流，教师答疑、解惑、指导。

情感态度与价值观：

渗透二次根式在实践中的运用，使学生知道学为所用，树立服务社会的思想。

（二）重 点:二次根式的基础知识回忆及灵活运用

（三）难 点:知识点的灵活运用

2. 教学过程：

考点梳理：

(一)、了解二次根式、最简二次根式的概念；

1、二次根式的定义：形如 （a≥0）的式子

2、二次根式有意义的条件：_____________________

3、最简二次根式：

同时满足两个条件：①、被开方数不含分母

②、被开方数中不含能开得尽方的因数或因式

分母有理化：将分母中含二次根式的式子化为分母中不含二次根式的式子，如：

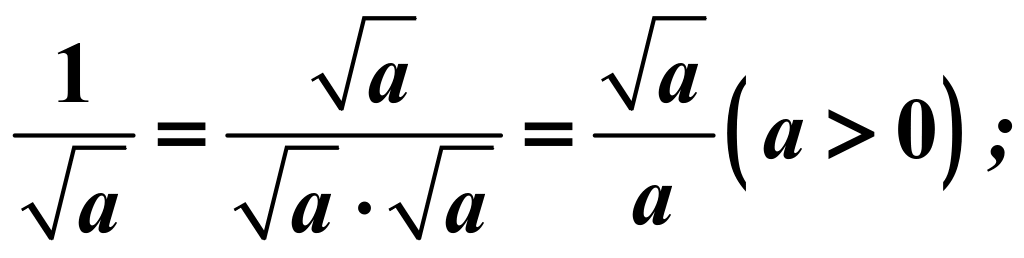
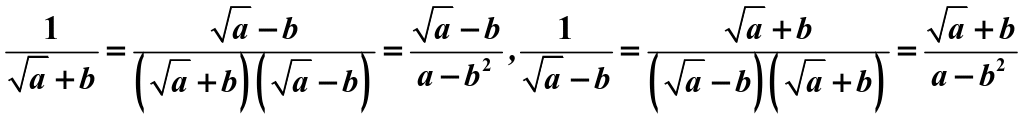
（二）1、了解二次根式(根号下仅限于数)加、减、乘、除运算法则，会用它们进行有关的简单四则运算；

2、能用有理数估计一个无理数的大致范围．

二次根式的运算

乘法： ＝______（a≥0，b≥0）

除法： （a≥0，b＞0）

加减法：先将二次根式化成最简二次根式，再将被开方数相同的二次根式进行合并

【温馨提示】在二次根式运算中，一般要把最终结果化为最简二次根式

1.先对二次根式平方

2.找出与平方后所得数字相邻的两个开得尽方的整数

3.对以上两个整数开方

4.确定这个二次根式的值在开方后所得的这两个整数之间

三、讲解练习：

1．二次根式 中的x的取值范围是(　　)

A．x＜－2 B．x≤－2

C．x＞－2 D．x≥－2

2．(2019甘肃)使得式子 有意义的x的取值范围是(　　)

A．x≥4 B．x＞4

C．x≤4 D．x＜4

3．下列计算正确的是(　　)

A．＋＝

B．2－＝

C．÷＝3

D．×(－)＝

4．下列计算正确的是(　　)

A．－＝ B．÷＝

C．×＝4 D．＝±15

5．(2019重庆)估计 ＋× 的值应在(　　)

A．5和6之间 B．6和7之间

C．7和8之间 D．8和9之间

6．实数a，b在数轴上的位置如图1所示，则化简－－的结果是(　　)

图1

A．2b B．2a

C．2(b－a) D．0

7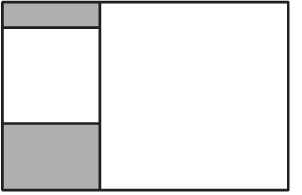．(2019淄博)如图1，矩形内有两个相邻的正方形，其面积分别为2和8，则图中阴影部分的面积为(　　)

A． B．2

C．2 D．6

8．设矩形的面积为S，相邻两边的长分别为a，b，已知S＝2，b＝，则a等于__________．

9．计算 ×－ 的结果是__________.

10．计算：×－2＝__________.

11．计算：＝__________.

12．计算：(1)×＝__________；

(2)＝__________.

13．计算：＋－×.

14、(2019大连)计算：(－2)2＋＋6.

15．化简：－3×＋＋(π＋1)⁰.

16．计算：(2－1)²－(－)÷.

17．(2019随州)“分母有理化”是我们常用的一种化简的方法，如：＝＝7＋4，除此之外，我们也可以用平方之后再开方的方式来化简一些有特点的无理数，如：对于－，设x＝－，易知＞，故x＞0，由x²＝(－)²＝3＋＋3－－2＝2，解得x＝，即－＝.

根据以上方法，化简＋－后的结果为(　　)

A．5＋3 B．5＋

C．5－ D．5－3

4. 布置作业

红枣卷第二卷

3