德州市教育科学研究院,山东 德州 253000
摘要:结构不良试题在2020年全国新课程I、Ⅱ(即山东卷、海南卷)首次出现,结构不良试题是在结构良好试题的基础上,将部分已知条件弱化,学生需先进行选择,然后解答,这对学生思维能力培养有着良好的导向作用。
关键词:结构不良;素养导向;高考题
1 结构不良高考试题出现的背景
“中国高考评价体系”,为高考内容改革指明了方向,为各学科制定命题标准提供了重要依据。高考评价体系总体框架是“一核四层四翼”,其中“一核”为考查目的,即立德树人、服务选才、引导教学;“四层”为考查内容,即核心价值、学科素养、关键能力、必备知识;“四翼”为考查要求,即基础性、综合性、应用性、创新性。
结构不良试题是针对结构良好试题而言的,结构良好问题有明确的已和条件和要达到的目标,有确定的计算方法。结构不良问题一般有三类:①已知条件明确,目标要求不明确;②已知条件不明确,目标要求明确;③已知条件与目标要求均不明确。2020新高考数学结构不良试题的引入,增强了试题条件的开放性,引导学生更加注重思维的灵活性及策略选择。结构不良试题具有很好的开放性,对数学理解能力、数学探究能力的考查能够起到积极的作用。
2 结构不良试题分析
例1:(2020新高考ⅠⅡ)在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求
这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求![]() 的值;若问题中的三角形不存在,说明理由.
的值;若问题中的三角形不存在,说明理由.
问题:是否存在![]() ,它的内角
,它的内角![]() 的对边分别为
的对边分别为![]() 且
且![]() ,______?
,______?
【分析】本题从试题的情境设置来说为课程学习情境,基础知识为三角函数与解三角形内容,所考查的必备知识为正弦定理,余弦定理;在基础性的层次方面考查了学生理性思维能力。学生要对条件进行选择,然后进行解答,无论选择哪一个条件,题目最终有自己的答案,要么存在符合条件的三角形,要么不存在,二者必居其一,故学生要相信自己,从自己所选条件出发,达到理想的彼岸。题目考查了逻辑推理,数学运算的学科素养。
解决路径:从已知条件出发,有两种方案,一是角化边利用余弦定理,得出三边的长度关系,然后再利用选择的条件进行分析判断和求解;二是利用诱导公式,两角和差公式,通过转化,得出角度之间的关系,然后进行分析判断和求解。通过解析,选择三者中任何一个,都能解决问题,选择①、②,最终的三角形是存在的,选择③,三角形不存在,而选择①、②,虽然三角形存在,但三角形边角关系不一样。
例2:(山东、海南新高考测试卷)在①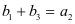 ,②
,②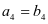 ,③
,③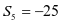 这三个条件中任选一个,补充在下面问题中,若问题中的k存在,求k的值;若k不存在,说明理由.
这三个条件中任选一个,补充在下面问题中,若问题中的k存在,求k的值;若k不存在,说明理由.
设等差数列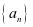 的前
的前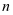 项和
项和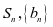 是等比数列,__________,
是等比数列,__________,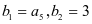 ,
,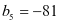 ,是否存在k,使得
,是否存在k,使得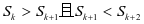 ?
?
【分析】本题的情境为课程学习情境,为等差数列与等比数列,所考查的必备知识为等差数列通项公式及前n项和公式,等比数列通项公式,考查了逻辑推理,数学运算等关键能力。
解决路径:方案一是从三个条件中任意选择一个,融入到已知条件,把此题变成结构良好试题解决;另一种方案是先从已知条件出发,得出结论,本题由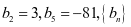 是等比数列,得出
是等比数列,得出 ,因为
,因为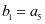 得
得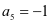 ,然后再对开放条件进行选择。通过解析,可以看出,选择三者中任何一个,都能解决问题,选择①③,k值均为4,选择②,k值不存在。
,然后再对开放条件进行选择。通过解析,可以看出,选择三者中任何一个,都能解决问题,选择①③,k值均为4,选择②,k值不存在。
例3.在①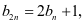 ②
②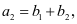 ③
③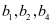 成等比数列这三个条件中选择符合题意的两个条件,补充在下面问题中,并求解。
成等比数列这三个条件中选择符合题意的两个条件,补充在下面问题中,并求解。
已知数列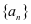 中
中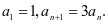 公差不等于0的等差数列
公差不等于0的等差数列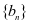 满足
满足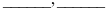 ,求数列
,求数列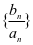 的前
的前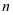 项和
项和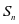 。
。
【分析】本题的情境仍然为课程学习情境,内容为等差数列与等比数列,所考查的必备知识为等差、等比数列通项公式,错位相减法求和,考查了数学抽象、逻辑推理、数学运算等关键能力。
解决路径:此题需先从已和条件入手,得出数列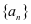 的通项公式,此时用到了等比数列通项公式;然后加以选择,若选择①②,在①中令
的通项公式,此时用到了等比数列通项公式;然后加以选择,若选择①②,在①中令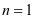 ,可得
,可得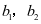 的方程组,从而得出
的方程组,从而得出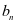 的通项公式;若选择②③,可得出数列
的通项公式;若选择②③,可得出数列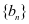 的公差,进而得出通项公式;若选择①③,得出矛盾。
的公差,进而得出通项公式;若选择①③,得出矛盾。
通过以上分析,可以得出结构不良试题要求考生能够根据条件,自主分析,得出命题,并解决问题,这种自主推断题甚至是开放题以后将成为新高考的热点。
3 结构不良问题的特点
3.1 高考数学试题呈现方式为文字符号结构或为文字符号图表(图形)结构,而具体情境分为三类,一是课程学习情境;二是探索创新情境;三是生活实践情境。从目前来看,结构不良试题和具体的情境相联系,一般是课程学习情境;
3.2 问题的开放条件类型比较多,三选一,三选二,四选三等等,涉及到的内容有三角,数列,立体几何、解析几何等等,这些类型在不同层次的试题中均有涉及;
3.3 存在多种评价标准,答案存在多样性,有的直接得出结论,有的得出结论但结论因选择条件不同而不同,有的是通过分析,模型不存在。
4 结构不良问题的解决思路
4.1 必备知识
解决结构不良问题首先要有知识储备,即必备知识,解决三角问题需要掌握三角函数的定义,诱导公式,和差公式,倍角公式,正余弦定理等;解决数列问题需掌握等差、等比数列的通项公式与前n项和公式等;对立体几何需掌握线面、面面之间的平行垂直关系,定理的应用等,储备的知识越多,越有助于提高问题解决能力。
4.2 合理途径
选择一个合适的解决方案,对问题解决会起到事半功倍的效果,要制订好解题策略,哪一个开放条件对你来说,比较熟悉,与题目已知条件更有关联性。是从开放的条件出发,将题目变成结构良好试题,还是先将已知条件进行梳理,再根据自己的知识储备对开放条件进行选择。
4.3 良好品质
良好的心理品质是一个人取得成功的前提,爱迪生曾言:“伟大的人物最明显的标志,就是他的坚强意志。”对问题解决要持有必胜的信念,要保持积极的情绪状态,相信在自己的能力范围内一定能够解决此类问题。
5 结构不良问题对当今教学的启示
5.1 加强“四基”教学,注重对必备知识的积累。万丈高楼平地起,基础的重要性如何强调也不为过,在高考考查要求中,基础性是其中之一,只有基础扎实,在面对各种问题时才能得心应手。而必备知识是指面对问题时,有效的分析问题解决问题所必须具备的知识。“四基”与必备知识是紧密关联的,在考查过程中,“四基”是通过必备知识呈现的。
5.2 与结构良好试题相比,结构不良试题给了学生更多的思考空间,内容考查灵活性强,只依靠刷题,题海战术已经不能胜任新的高考形势,考生务必提升独立思考、独立分析和解决问题的能力。
5.3 结构不良试题大多是在考试试题中出现,而在课堂教学中真正得到落实的还不够,教师要重视开放题的功能,关注结果,重视过程,注重对数学理性思维的培养,充分培养学生的核心素养。
参考文献
[1]中华人民共和国教育部.普通高中数学课程标准(2017版)[M].北京:人民教育出版社,2018.
[2]教育部考试中心.中国高考评价体系说明[M].北京:人民教育出版社,2019.
[3]张侨平,唐彩斌.落实素养为本的数学开放题教学[J].数学教育学报,2019,28(6):61-64
[4]任子朝、陈昴、黄熙彤,等.高考数学新题型试卷质量分析研究[J].数学教育学报,2019,28(1):1-7.

1