沈阳理工大学 装备工程学院,沈阳 110159
[摘要]:本文采用耦合欧拉—拉格朗日方法分析了不同的头部外形与长径比、初始速度的运动体穿越冰水混合物诱发的空化效应。得到了运动体穿越冰水混合物的时间速度曲线。结果表明:在相同的速度下,头部形状为截锥形的运动体相对于圆柱形可以减弱包络在其自身周围空腔与空泡扩散的速度,圆柱形运动体周围形成空泡的直径大于截锥形;大长径比的运动体可以维持自身周围空腔的相对稳定;运动体进入冰水混合物的初始速度可以直接影响空腔的形成、扩散,空泡的数量。构建了实验测试系统,开展了实验验证,数值模拟与实验结果基本吻合。
[关键词]:冰水混合物;空腔;空泡;空化效应
0引言
随着潜射技术的不断发展,潜射弹道导弹不仅要适应水中单相介质运动,更需要适应冰与水两相介质混合运动。运动的导弹会对介质接触面产生剧烈的扰动,可能使得导弹周围流场区域的瞬态压力低于某临界饱和蒸汽压,液体发生相变,可能诱发空泡的产生。而空泡一系列的演化过程,会造成导弹结构、运动姿态与速度的改变。
在学术界,对于水下航行体出水并伴随空泡的形成、扩张、收缩、 溃灭的演化过程已进行大量的研究。Mirzaei[1]采用理论建模的方法研究水下高速运动弹体的飞行和弹道稳定性。黄晨光[2]研究水下航行体出水空泡溃灭的过程。张伟,齐亚飞[3]等开展了在弹体高速入水过程中弹体及空泡特性的研究。黄威[4]采用实验方法,开展了高速刚性弹体侵彻有限容积水箱,观测到了在弹体的周围会产生水锤效应,并进行了由它引起的初始冲击波与空泡相关特性的研究。魏英杰[5]采用数值模拟方法研究了潜射导弹垂直发射上升过程中的空泡流。Liu[6]仿真分析了船舶与冰山碰撞的外部与内部动力学的问题。郭春雨[7]运用近场动力学方法,开展了潜艇破冰上浮过程及冰载荷的动态特性数值模拟。本文分析了运动体与冰水混合物相互作用诱发的空化效应并进行了数值模拟与实验验证。
1运动体穿越冰水混合物诱发空化效应的数值模拟
1)构建运动体穿越冰水混合物数值模拟模型
(1)建立冰水混合物与运动体的几何模型
几何模型包括水区域,碎冰与运动体,如图1所示。
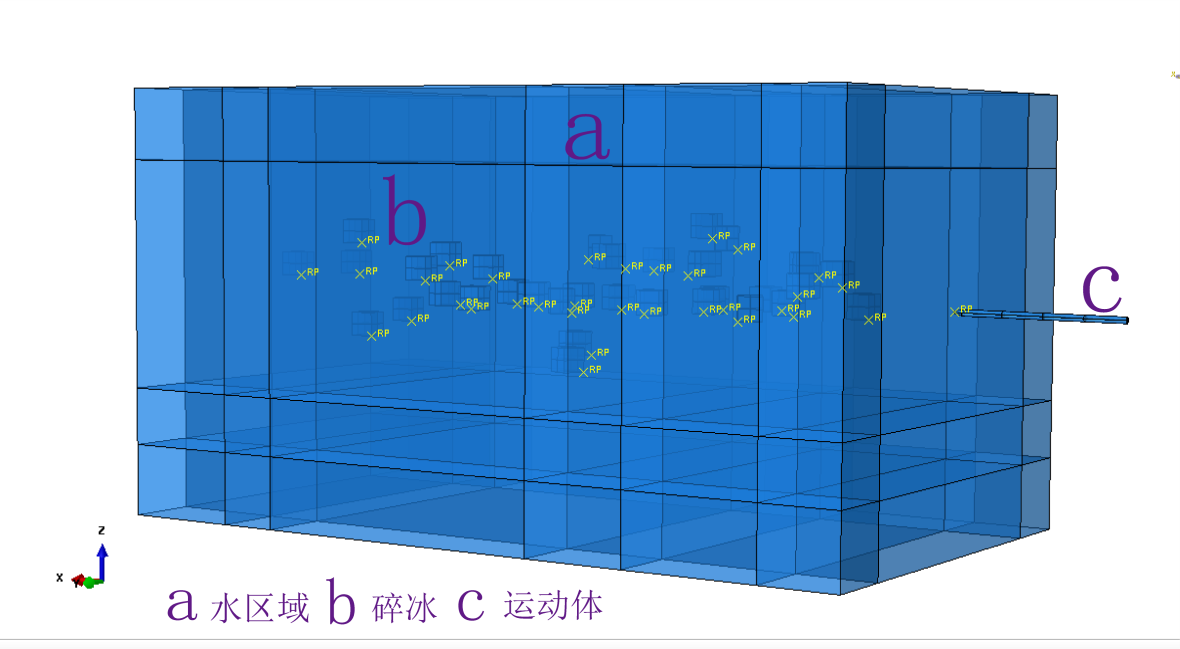
图1运动体穿越冰水混合物的装配模型
水的区域为800×500×500mm,采用欧拉体。碎冰为20×20×20mm,数量35个,采用立方体,运动体的头部形态分别为截锥形与圆柱形。
(2)冰水混合物与运动体的材料参数
碎冰、运动体的材料参数如表1所示。在冰水混合物中水的材料参数采用状态方程:
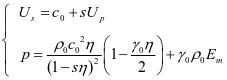
式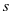
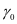
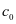 中: 为波速、 、 为材料系数,详细参数如表2所示。
中: 为波速、 、 为材料系数,详细参数如表2所示。
表1碎冰与运动体的材料参数
| Density (kg/ m3) | Elastic (MPa) | Poisson’s ratio |
碎冰 | 846 | 9360 | 0.33 |
运动体 | 4529 | 118600 | 0.33 |
| Density (kg/ m3) | ( | Viscosity(Pa.s) |
水 | 1000 | 1483 0 0 | 0.00103 |
表2水的材料参数
(3)边界条件
对水域的底面进行了固定约束,四个侧面的边界设定速度为0。
(4)模型的网格划分
模型的网格划分如图2所示,其中水域模型采用八结点欧拉体单元网格,碎冰模型采用八结点六面体单元网格,运动体模型采用八结点六面体单元网格。


(a) 水域模型 (b) 碎冰模型
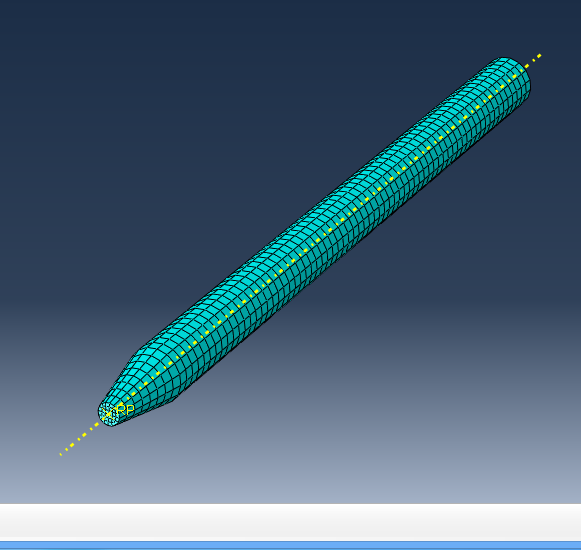

(c) 长径比为15.5运动体模型 (d)长径比为28.8运动体模型
图2模型网格划分
(5) 求解器
运动体穿越冰水混合物的模拟过程采用非线性显式求解。
2)运动体穿越冰水混合物诱发的空化效应分析
运动体与冰水混合物相互作用可能有诸多不同因素诱发空化效应,主要影响因素是运动体的头部形状、长径比、进入冰水混合物的初始速度。
(1)头部形状对诱发空化效应的影响分析
分别构建长径比(15.5)相同、不同头部形状(截锥形、圆柱形)运动体的计算模型并计算求解,图3显示头部形状分别为截锥形与圆柱形的运动体,以相同的速度45m/s穿越冰水混合物在其自身周围形成空腔的演化过程。

图3截锥形与圆柱形在其自身周围形成空腔与空泡的演化过程
在图3中M代表截锥形运动体的所在位置,N代表圆柱形运动体的所在位置,Q区域代表空腔断裂区域,Z区域代表空泡形成区域,t=0.006s时在图3(a)、3(b)中截锥形与圆柱形的运动体周围已经形成了包络其自身的空腔,分别在Q区域出现空腔断裂;t=0.009s时二者在图3(c)、3(d)中Z区域出现形状大小不等空泡,前者与后者在Z区域形成空泡的直径平均之比约为0.28;t=0.018s时二者在图3(e)、3(f)中Z区域出现了空泡的扩散,后者在Z区域扩散剧烈;t=0.030s时二者在图3(g)、3(h)中Z区域出现了空泡的收缩并形成多个大小不等的空泡,前者与后者在Z区域形成空泡的直径平均之比约为0.78。图4显示截锥形与圆柱形运动体周围形成空腔的外貌特征。
(a)截锥形运动体 (b) 圆柱形运动体
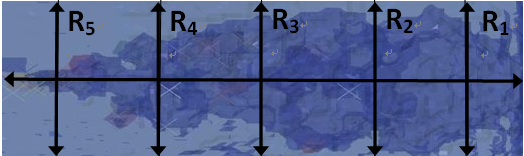
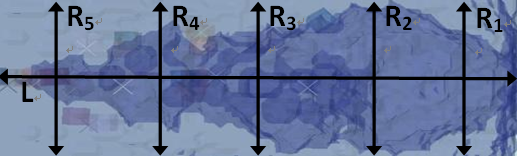
图4截锥形与圆柱形运动体周围形成空腔的外貌特征
如图4所示,(a)、(b)分别为截锥形与圆柱形运动体在其周围形成的空腔外貌特征,前者空腔外貌特征头部收缩,尾部凸起,大体呈现截锥形,外围轮廓凹凸不平,后者的头部收缩,尾部扩散。表3显示二者周围空腔的直径尺寸变化,其中R1、R2、R3、R4、R5表示空腔直径演化的距离,L表示空腔的长度,截锥形周围空腔的直径小于圆柱形。
表3不同时刻截锥形与圆柱周围形成空腔的直径尺寸变化
| t(s) | L(mm) | R5(mm) | R4(mm) | R3(mm) | R2(mm) | R1(mm) |
截 | 0.006 | 63.226 | 0 | 0 | 0 | 14.545 | 15.455 |
0.007 | 97.684 | 0 | 0 | 0 | 22.375 | 19.872 | |
0.018 | 129.381 | 0 | 17.879 | 20.150 | 25.618 | 21.318 | |
0.031 | 164.524 | 10.307 | 23.638 | 25.123 | 29.121 | 24.091 | |
圆柱形 | 0.006 | 70.910 | 0 | 0 | 6.667 | 12.487 | 13.226 |
0.007 | 95.759 | 0 | 0 | 12.576 | 18.325 | 17.106 | |
0.018 | 142.440 | 6.068 | 18.229 | 23.871 | 22.065 | 21.258 | |
0.003 | 170.940 | 9.230 | 24.652 | 26.194 | 25.961 | 25.982 |
图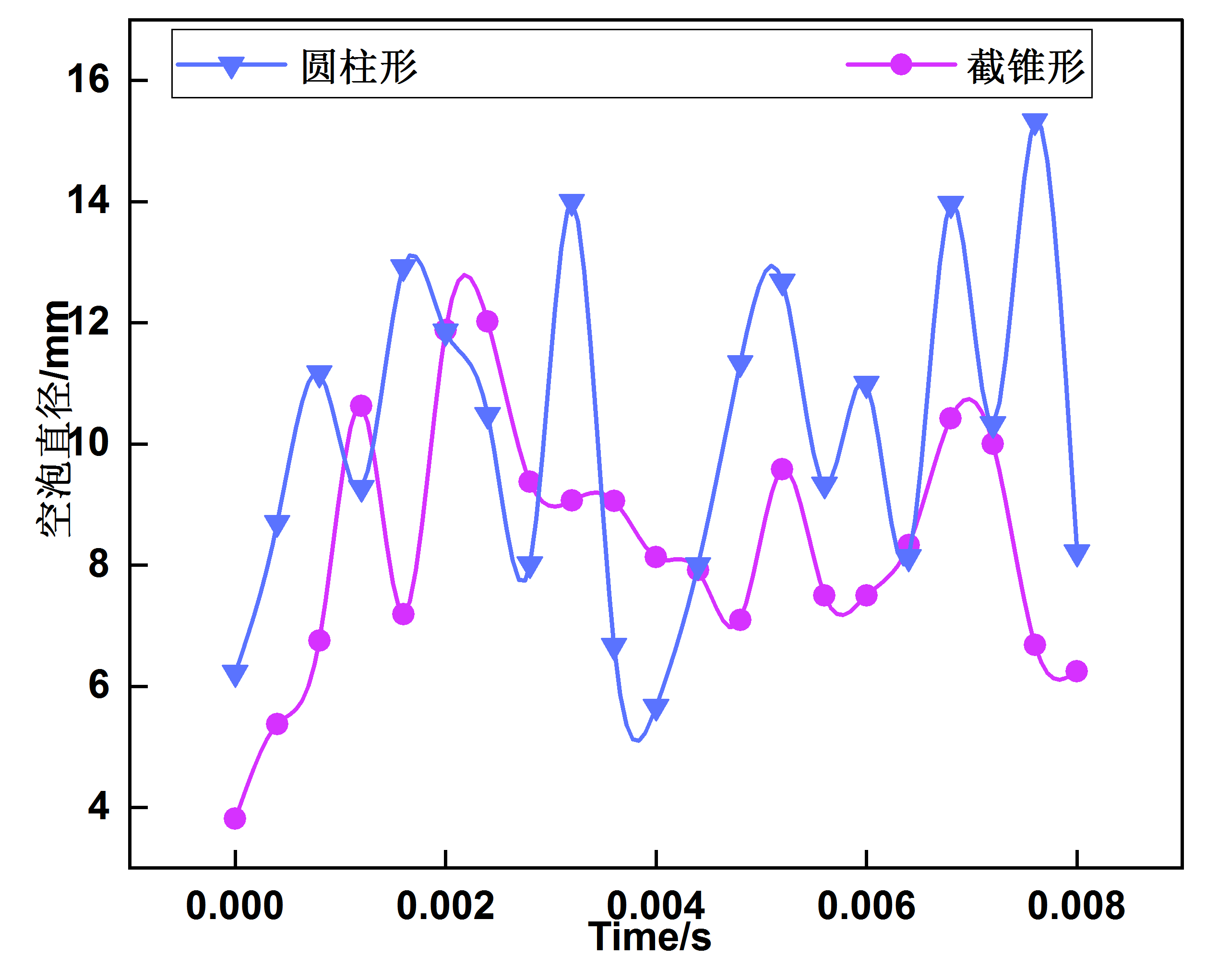 5显示不同时刻截锥形与圆柱形运动体在其自身周围形成空泡的直径尺寸,前者形成空泡的直径小于后者。
5显示不同时刻截锥形与圆柱形运动体在其自身周围形成空泡的直径尺寸,前者形成空泡的直径小于后者。
图5不同时刻圆柱形与截锥形在其自身周围形成空泡的直径尺寸
通过对比分析了相同速度与长径比,头部外形特征为截锥形与圆柱形运动体穿越冰水混合物过程中在各自周围形成空腔的演化过程、不同时刻空腔的直径尺寸,前者在其周围形成空腔的直径小于后者,主要是因为后者撞击碎冰对水产生剧烈的扰动,使得在其自身周围空腔的扩散速度高于前者,二者形成空腔体积平均之比约为0.83。
(2)长径比对诱发空化效应的影响分析
构建头部为圆柱形、长径比分别为28.8、15.5运动体的计算模型并求解计算,以相同的速度76m/s穿越冰水混合物。图6显示不同长径比运动体在其周围形成空腔的演化过程。
长 | 长径比15.5 |
| |
图6不同长径比运动体形成空腔的演化过程
如图6所示,在图6、6中M代表长径比为28.8运动体的所在位置,N代表长径比为15.5的所在位置,Q区域代表空腔断裂区域,Z区域代表空泡形成区域,t=0.002s时在图6(a)、6(b)中长径比为28.8与15.5运动体的周围已经形成了包络其自身的空腔,各自分别在Q区域出现了空腔的断裂;t=0.006s时二者在图6(c)、6(d)中Z区域出现不同形状的空泡,前者与后者形成空泡的直径平均之比约为0.76;t=0.008s时二者在图6(e)、6(f)中Z区域出现了空泡的扩散,后者在Z区域空泡的扩散剧烈;t=0.030s时二者在图6(g)、6(h)中Z区域出现了空泡的收缩,前者形成大小不等空泡的数量小于后者。图7显示不同长径比运动体周围形成空腔的外貌特征。
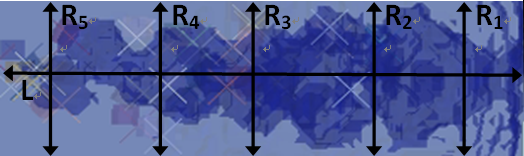
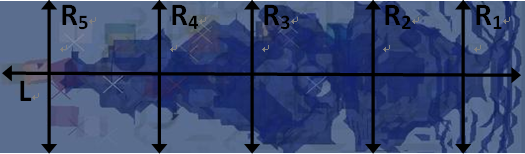
长径比28.8 (b) 长径比15.5
图7不同长径比运动体周围形成空腔的外貌特征
表4不同时刻空腔直径尺寸
长径比 | t(s) | L(mm) | R5(mm) | R4(mm) | R3(mm) | R2(mm) | R1(mm) |
28.8 | 0.002 | 80.000 | 0.000 | 0.000 | 0.000 | 4.074 | 11.852 |
0.006 | 165.556 | 0.000 | 7.407 | 19.630 | 29.632 | 13.444 | |
0.008 | 190.006 | 1.852 | 13.411 | 27.407 | 36.667 | 15.889 | |
0.010 | 208.148 | 10.741 | 22.212 | 34.444 | 34.815 | 12.037 | |
15.5 | 0.002 | 70.370 | 0.000 | 0.000 | 0.000 | 0.000 | 13.704 |
0.006 | 134.815 | 0.000 | 8.889 | 26.296 | 37.407 | 15.519 | |
0.008 | 174.444 | 5.185 | 15.111 | 42.137 | 41.852 | 12.963 | |
0.010 | 181.481 | 11.111 | 29.259 | 54.444 | 55.185 | 10.296 |
如图7所示,(a)、(b)分别为长径比为28.8与15.5运动体在其周围形成空腔的外貌特征,前者的空腔外貌特征头部凹陷,尾部凸起,后者的空腔外貌特征大体呈现梭状。表4显示了空腔的直径尺寸变化,其中R1、R2、R3、R4、R5表示空腔直径演化的距离,L表示空腔的长度,大长径比周围空腔的直径小。
通过对比分析了在相同速度,不同长径比的圆柱形运动体穿越冰水混合物在各自周围形成空腔的演化过程,总体上大长径比的运动体能够维持在其自身周围空腔的相对稳定。
(3)不同初始运动速度对诱发空化效应的影响分析
构建长径比相同、头部形状为截锥形运动体的计算模型并求解计算,分别以初始76 m/s、52m/s运动速度穿越冰水混合物。
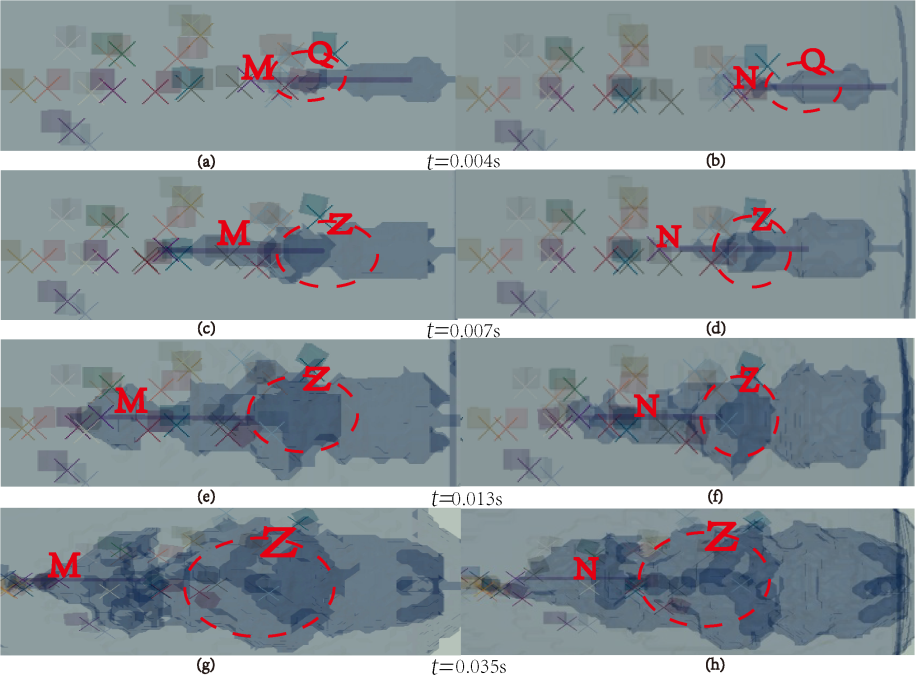
图8不同初始速度的运动体在其自身形成空腔的演化过程
如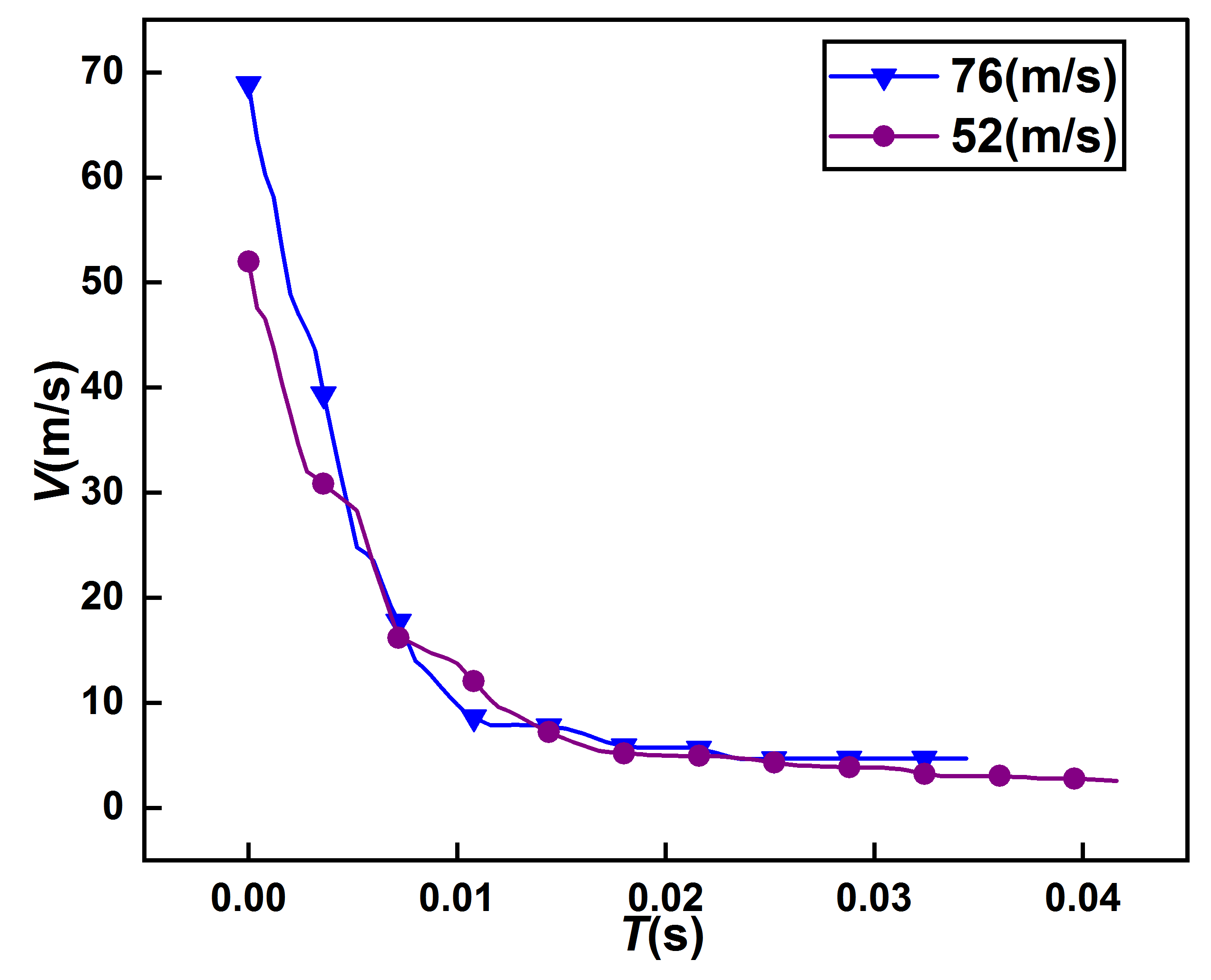 图8所示,左边与右边分别显示初始速度为76m/s与52m/s运动体形成空腔的演化过程,其中M代表前者的所在位置,N代表后者的所在位置,Q区域代表空腔断裂区域,Z区域代表空泡形成区域,t=0.004s时在图8(a)、8(b)中Q区域,前者与后者周围已经形成了包络其自身的空腔;t=0.007s时各自在图8(c)、8(d)中Z区域出现形状大小不等的空泡,前者与后者形成空泡的平均直径之比约为0.28;t=0.013s时各自在图8(e)、8(f)中Z区域出现了空泡的扩散,前者空泡扩散范围大于后者,t=0.035s时各自在图8(g)、8(h)中Z区域出现了空泡的收缩与扩散并形成多个大小不等的空泡,后者空泡明显,数量大于前者。图9显示不同初始速度的运动体穿越冰水混合的时间速度曲线。
图8所示,左边与右边分别显示初始速度为76m/s与52m/s运动体形成空腔的演化过程,其中M代表前者的所在位置,N代表后者的所在位置,Q区域代表空腔断裂区域,Z区域代表空泡形成区域,t=0.004s时在图8(a)、8(b)中Q区域,前者与后者周围已经形成了包络其自身的空腔;t=0.007s时各自在图8(c)、8(d)中Z区域出现形状大小不等的空泡,前者与后者形成空泡的平均直径之比约为0.28;t=0.013s时各自在图8(e)、8(f)中Z区域出现了空泡的扩散,前者空泡扩散范围大于后者,t=0.035s时各自在图8(g)、8(h)中Z区域出现了空泡的收缩与扩散并形成多个大小不等的空泡,后者空泡明显,数量大于前者。图9显示不同初始速度的运动体穿越冰水混合的时间速度曲线。
图9不同初始速度的运动体穿越冰水混合的时间速度曲线
如图9所示,时间速度曲线呈现的波动点,主要是运动体撞击碎冰产生的影响。对比分析不同初始速度的运动穿越冰水混合物在其自身周围形成空腔的演化过程与相同距离下的时间速度曲线,在碎冰与水的混合物中,运动体进入冰水混合物的初始速度对空化效应的影响极大,可以直接影响空腔扩散的速度与空泡的数量。
2 运动体穿越冰水混合物的实验验证
(1)构建实验测试系统
运动体穿越冰水混合物的模拟实验在辽宁省瞬态物理力学与能量转换材料重点实验室进行。图10为实验测试装置。
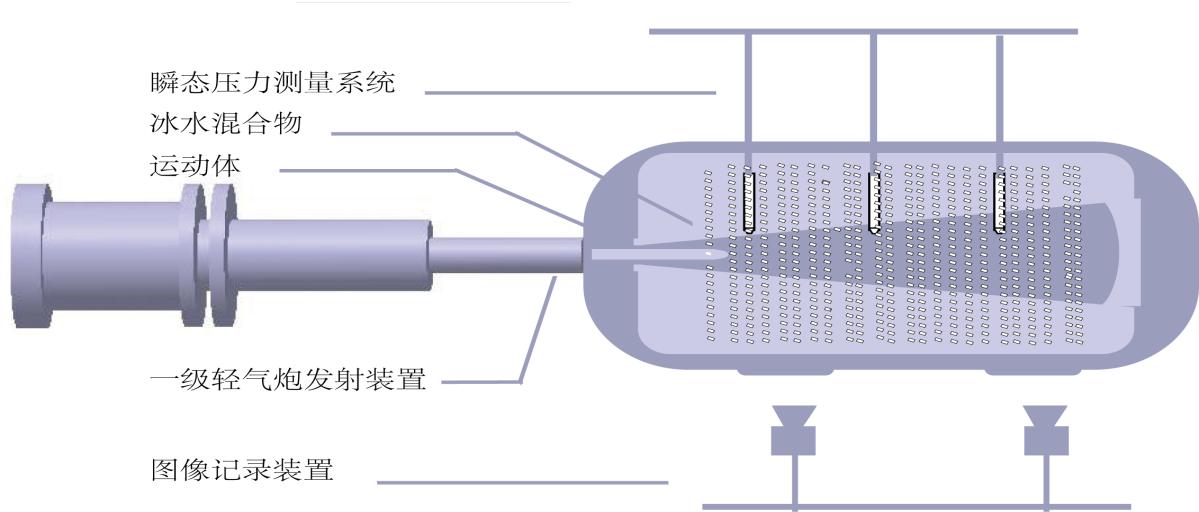
图10实验测试装置
如图10所示,实验的模拟测试系统主要包括:一级轻气炮发射装置,瞬态压力测量系统,高速摄像机图像记录装置,冰水混合物实验箱等。各部分主要功能如下描述:
1)一级轻气炮发射装置主要由气室,电磁阀,发射管等组成,通过调节气室压力的大小,驱动不同形状的运动体以不同的速度穿越冰水混合物。
2)瞬态压力测量系统包括动压传感器,压力时程数据采集与处理系统等组成,主要采集在冰水混合物中不同区域受到来自由运动体撞击水面形成冲击的压力时程。
3)图像记录装置包括高速摄像机,图像处理系统,主要观测运动体在冰水混合物中流场的运动轨迹和空腔的演化趋势,计算得出运动体在冰水混合物的时间速度曲线。
(2) 实验模型实物图与参数
如图11所示,显示实验模型实物图,表5显示实验模型参数。


图11实验模型实物图
表5实验参数
序号 | 头部外形 | 质量(g) | 长径比 | 入水速度(m/s) |
1 | 截锥形 | 13.458 | 28.80 | 76 |
(2)运动体穿越冰水混合物数值模拟与实验观测的对比
图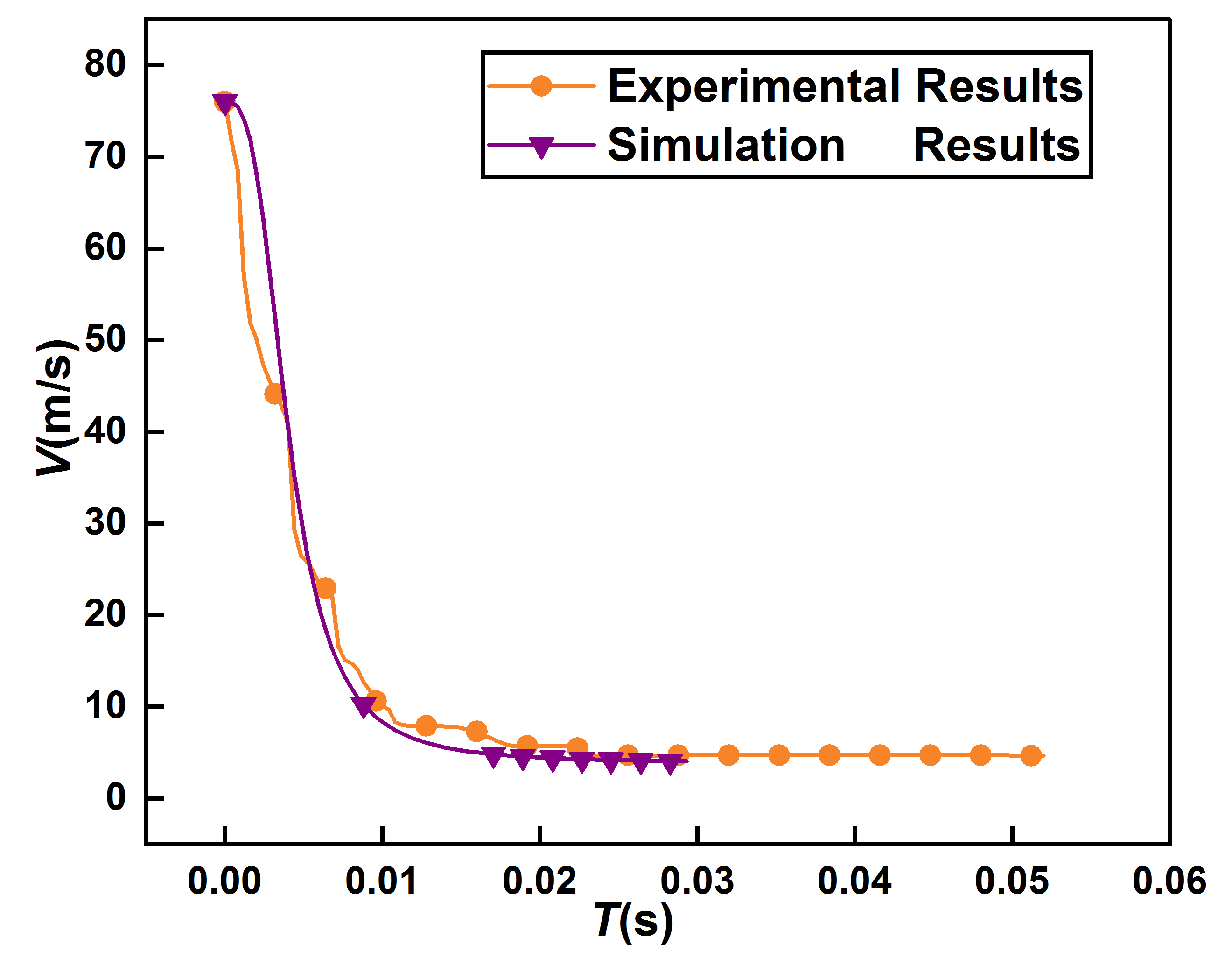 12是实验采集与数值模拟计算得到运动体穿越冰水混合物时间速度曲线的对比,图13左边为用高速摄像机记录的实验图像,右边为数值模拟结果,运动体穿越冰水混合物会形成包络其自身周围的空腔,实验图像与数值模拟形成空腔的外貌特征基本吻合。验证了数值方法的可行性,进而为研究空泡的微观演化以及引发的空化效应。图12为实验与数值模拟运动体穿越冰水混合物时间速度曲线对比。
12是实验采集与数值模拟计算得到运动体穿越冰水混合物时间速度曲线的对比,图13左边为用高速摄像机记录的实验图像,右边为数值模拟结果,运动体穿越冰水混合物会形成包络其自身周围的空腔,实验图像与数值模拟形成空腔的外貌特征基本吻合。验证了数值方法的可行性,进而为研究空泡的微观演化以及引发的空化效应。图12为实验与数值模拟运动体穿越冰水混合物时间速度曲线对比。
图12实验与数值模拟运动体穿越冰水混合物时间速度曲线对比
| | | |
(a)t=0.0016s | |||
| | | |
(b)t=0.0028s | |||
| | | |
(c)t=0.0042s | |||
| | | |
(d)t=0.0081s | |||
图13实验记录图像与数值模拟结果
3结论
1)相对于头部形状为圆柱形,截锥形的运动体可以减弱空腔与空泡的扩散速度。减缓了由空泡的溃灭引发空化效应产生的可能性。
2)大长径比的运动体可以维持在其周围形成空腔的相对稳定性,使的空化效应相对稳定。
3)运动体进入冰水混合物的初始速度可以直接影响空腔扩散的速度与空泡的数量,空泡的数量直接影响空化效应的剧烈程度。
4)数值模拟结果与实验结果基本吻合。
参考文献
[1] Mirzaei M, Alishahi M M, Eghtesad M. High-speed underwater projectilesmodeling: a newempirical approach[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2015, 37(2):613-626.
[2] 黄晨光. 航行体垂直出水载荷与空泡溃灭机理分析[J]. 力学学报, 2012, 44(2):39-48.
[3] 张伟,齐亚飞等.弹体高速入水弹道稳定特性实验研究[J].爆炸与冲击. 2009,83(1):51-59.
[4] 黄威.高速弹体水平入水特性研究[J].哈尔滨工业大学学报,2014,46(7):81-86.
[5] 魏英杰,闵景新,王 聪等. 潜射导弹垂直发射过程空化特性研究[J]. 工程力学,2009, 26(7):251-256.
[6] LIU Z H. Analytical and numerical analysis of iceberg collisions with ship structures[D]. Norway: Norwegian University of Science and Technology,2011:235.
[7] 郭春雨,王超等. 潜艇破冰上浮近场动力学模型[J].中国舰船研究,2018,13(2):51-59.
[8] KARNA T,KAMESAKI K,TSUKUDA H. A numeri⁃cal model for dynamic ice-structure interaction[J].Computers and Structures,1999,72(4/5):645-658.
[9] 张健,张淼溶,万正权.冰材料模型在船-冰碰撞结构数值模拟中的应用研究[J].中国造船,2013,36(4): 100–107.
[10] 郭天同.冰水固流转化理论研究[D].青岛:青岛科技大学,2011.
[11] KARNA T,KAMESAKI K,TSUKUDA H. A numeri⁃cal model for dynamic ice-structure interaction[J].Computers and Structures,1999,72(5): 645-658.
[12] YE L Y. Peridynamic model for submarine surfacing through ice[J]. Chinese Journal of Ship Research,2018,138(4): 51-59.
[13]Fu Hui-ping,Lu Chuan-jing,Li Jie. Numerical Research on Drag Reduction Characteristics of Supercavitating Body of Revolution. Journal of Ship Mechnics,2004,6(3):179-205.
[14] LAU, MLAWRENCE K P,ROTHENBURG L. Dis⁃crete element analysis of ice loads on ships and struc⁃tures[J]. Ships and Offshore Structures,2011,6(3):211-221.
[15] 张振华.水下爆炸冲击波的数值模拟研究[J].爆炸与冲击,2004,24(2):182- 189.
[16] 张洪雨.冰期船舶下水试验研究[J].中国造船,2013,54(2):62–68.
[17] 丛敏.美国海军的超空泡研究计划[J].飞航导弹,2009,60(1):17–20.
[18] 李根生,沈晓明,施立德.空化和空蚀机理及其影响因素[J]. 石油大学学报(自然科学版),1997,21(1):97–102.