探地雷达在隧道衬砌挡头模板处空洞检测中的正演模拟应用研究

探地雷达在隧道衬砌挡头模板处空洞检测中的正演模拟应用研究

周斌

中铁西南科学研究院有限公司 成都 611731

摘 要：隧道衬砌挡头模板空洞是衬砌检测中最常出现的空洞，识别挡头模板空洞波形特征，判断空洞埋深和规模是衬砌检测的重要内容。通过基于时域有限差分的数值模拟方法，正演探地雷达波形在隧道衬砌空洞中的传播规律，分析总结了衬砌挡头模板空洞的雷达波反射特征，计算空洞埋深，并将模拟结果指导衬砌检测的工程实践，取得了良好的效果，说明数值模拟是探地雷达波形识别的一种有效手段。

关键词：探地雷达；波形特征；数值模拟；衬砌空洞

1 引 言

2004国家《中长期铁路网规划》国务院审议通过标志着我国铁路新一轮大规模建设的开始。铁路隧道是铁路线路组成的重要部分，隧道施工质量直接影响到将来铁路运营的通畅和安全，隧道衬砌病害是困扰铁路快速发展的一个关键因素。衬砌挡头模板空洞是在泵送混凝土隧道衬砌施工过程中，两个相邻衬砌循环的邻接处，后一衬砌挡头模板处形成的空洞，此类空洞最常出现在衬砌拱顶。在隧道衬砌空洞检测中，隧道衬砌挡头模板空洞是衬砌空洞的主要形态。因此研究衬砌挡头模板空洞的探地雷达波形特征，判断挡头模板空洞的埋深和规模具有重要的意义。

地质雷达检测隧道衬砌缺陷领域，国外的研究结合了工程实践和实验室模拟，并且不断改进雷达软硬件技术，取得了一定的成果^[1]。在美国，有一个研究小组于2000年做了探地雷达用于检测隧道病害的实验模拟研究^[2]，在日本，东京大学作了探地雷达用于钢筋网定位以及空洞探测的室内模拟研究^[3]，铁道第三勘察设计院的薄会申在长期的探地雷达用于铁路隧道衬砌检测的工程实践中，总结了主要的衬砌病害的雷达检测图形特征^[4], 长沙铁道学院的高燕希指导研究生刘胜峰，张春宇,杨进，宁黎磊做了探地雷达用于隧道衬砌检测的室内模拟，主要模拟了衬砌空洞以及研究了混凝土龄期和介电常数的关系^[5,6,7,8]。

探地雷达资料解释中，雷达波形能更精确的显示反射同相轴，绕射，空洞多次反射等特征，从而有助于对目标体得识别和其埋深与规模的计算，国内外多通过模型实验模拟来总结目标体波形特征。本文通过数值模拟，正演了隧道挡头模板空洞的探地雷达探测情况，总结了衬砌空洞的雷达波形特征，并将其用于指导衬砌检测的工程实践，取得了较好的效果。

2 正演原理

2.1 麦克斯韦方程

探地雷达工作中发射的是电磁波，雷达正演模拟的问题就是解特定条件下的麦克斯韦方程组的问题，通常情况下，麦克斯韦方程很难得到解析解。在1966年，美国学者K.S.Yee,通过引入Yee元胞，初步提出了解麦克斯韦偏微分方程的方法^[9]，后来经过不同学者对该方法进行了完善，提出了解稳定条件以及改进边界约束条件，发展成时域有限差分正演方法。

为了模拟雷达波形在隧道衬砌中的传播情况，选择雷达波TM模式在 平面上的传播（TM_z）。TM模式下，垂直于模拟横截面方向上没有磁场。二维TM_z模式的解可由解麦克斯韦方程组得到，在这里，采用时域有限差分方法，通过Yee网格剖分，运用有限差分思想，来逐步得到二维TM模式下麦克斯韦方程组的数值解。

二维TM模式下时域有限差分麦克斯韦方程组由以下公式组成：

（1）

上式中， E是电场强度， H是磁场强度， 是等效磁阻率， 是电导率。假设材料是线性、各向同性的。

时域有限差分方法将电磁空间用Yee元胞填充，在Yee元胞中，电场和磁场互相交错，每一个电场强度量被其相邻的磁场量包围，同理，每一个磁强度量也被各个方向的电场强度量包围。对于离散空间，有限差分方程涉及的是指定点的泰勒线性展开式的值，该方法提供了偏微分方程的近似解。那么式（1）中函数的空间偏导数可由式（2）计算

（2）

假设没有点激发源，介质的磁导率和真空中的磁导率一致（ ，很多非铁磁材料的的磁导率都属于这种情况）。假设空间步进在横纵坐标是同一个值（ ），则式（1）可以消除梯变增量而得到进一步简化。由于金属等良导体的电导率无穷大，因此，在计算中，当介质中含有良导体时，良导体的电场强度为零。

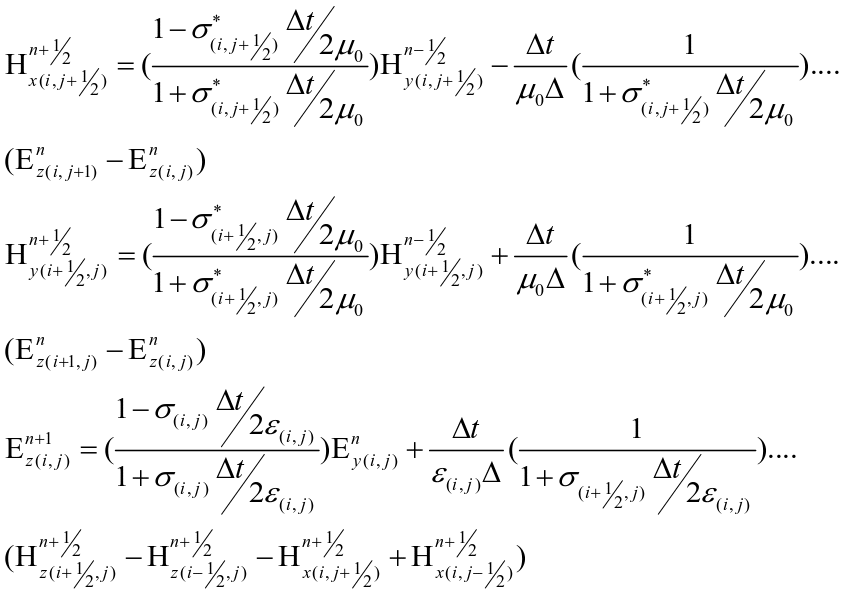（3）

式（3）即为二维时域有限差分TM模式，对时间因子的麦克斯韦偏微分方程。

2.2 稳定条件

对于给定的初始条件，偏微分方程的解由于数值的不稳定而导致计算值没有约束的增加。而在计算中，系统中的误差一定不能累积。在有限差分公式中，我们通过柯朗公式，运用空间步进来约束时间步进。

在二维情况下，

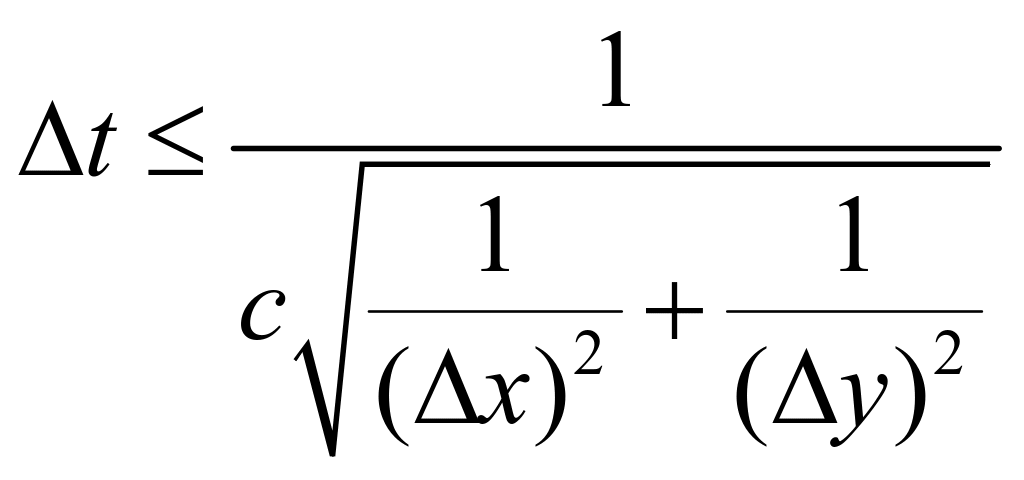（4）

2.3 边界条件

Berenger于1994年提出了完全匹配层（Perfectly Matched Layer:PML）^[10]，它可以完全吸收真空中以任何频率和角度入射的电磁波。

假设围绕目标模拟区域有一层材料能够完全吸收波形并且不产生反射。该材料的磁导率和电导率分别是 ， ，由于该材料能够吸收入射波，因此是复数，其阻抗可由下式得到：

（5）

根据电磁波传播原理，从真空入射进入完全匹配层的入射波的反射系数为

（6）

其中， ， 分别为真空的磁导率和电导率。

要使完全匹配层边界不产生反射，则必须使 ，即要求 ，即为：

， （7）

计算可得：

2.4 程序实现

按照时域有限差分解麦克斯韦偏微分方程的思路，采用Matlab语言，编制了隧道衬砌空洞的二维正演程序，以研究探地雷达在探测隧道衬砌空洞的有效性以及探地雷达的波形特征。程序的流程为：设定模拟区域几何尺寸以及电磁参数，进行Yee网格剖分，输入雷达天线发射器参数，设定天线收发位置、步进长度，进行正演计算，以及图像输出。

3 模型模拟

根据电磁波正演的稳定条件以及采样定理，用于Yee网格剖分的区域是 的矩形区域，设定Yee的空间步进 ，时间步进 ，时间窗口 。隧道衬砌的尺寸为 ，位于模拟区域的下方，其中，衬砌和初期支护的界面，有一层宽度为0.05 cm的接触面，其由空气填充，模拟衬砌的预留变形空间；挡头模板空洞的位置位于衬砌中挡头模板处，其外形一般为三角状。

对于空洞的水平起止位置，在波形图中，第一道由空洞引起的多次反射波是第33道雷达波，最后一道由空洞引起的多次反射波是第53道雷达波。在已知模型第一道接受波处于0.105 米以及道间距为0.02 米的前提下，可求得空洞的宽度：

空洞起始点水平坐标：

空洞终止点水平坐标：

模型中空洞的宽度为：0.40 m，可知误差为：

对于空洞的埋深，分别在波形图上B部分找到挡头模板三角状空洞与衬砌混凝土分界面的反射同相轴起止位置，第一道由空洞引起的多次反射波即第33道雷达波的空洞反射时间为6ns，第一道由空洞引起的多次反射波即第53道雷达波的空洞反射时间为3ns，在已知波速的情况下，可计算得：

空洞埋深最大位置：

空洞最浅埋深位置：

模型中空洞的最大埋深为：0.32 m，可知误差为：

考虑到正演模拟的截断误差和逼近误差，这个误差也是在正常范围内的。可知，雷达在探测隧道挡头模板空洞，并计算空洞埋深和规模宽度上，是可行的。

4 结论与建议

（1）时域有限差分方法模拟探地雷达波形在挡头模板衬砌空洞传播的特征可以归纳如下：在空洞处反射强反射，且有多次反射特征，同相轴明显错乱，波形振幅大，能力强；

（2）正演模拟对隧道衬砌检测的雷达图像识别具有重要的指导作用，根据衬砌缺陷的电磁参数，建立精细的，准确的模型，是总结正演雷达波形的前提；

（3）和物理模型实验相比，正演模拟的波形特征更具体，更能体现多次反射，单点绕射，双曲线弧线形成等经典波形传播规律。

参考文献

[1] 薄会申.地质雷达技术实用手册[M].北京:地质出版社,2006

[2] 刘胜峰.地质雷达应用于公路隧道衬砌无损检测的试验研究[D].长沙：长沙理工大学硕士论文，2007

[3] 张春宇 公路隧道衬砌介电常数理论实验与应用研究[D].长沙：长沙理工大学硕士论文，2009

[4] 杨进 隧道衬砌质量评价与探地雷达无损检测模型实验研究[D].长沙：长沙理工大学硕士论文，2008