沈阳师范大学教育硕士研究生院 辽宁省沈阳市 110034
摘要
二项式定理是高中课程中计数原理一章的重要内容,《普通高中数学课程标准(2017年版)》对二项式定理的教学目标的要求是能用多项式运算法则和计数原理证明二项式定理,会用二项式定理解决与二项展开式有关的简单问题。本文以“一师一课”中由河南省安阳县实验中学的数学教师讲授的定理引入和证明片断为依据,进行评析。
关键词:二项式定理 组合 案例
案例
一、定理的引入
教师:首先我们先回顾一下,以下两个多项式是如何展开的。PPT展示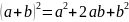 .
.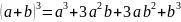 。展开
。展开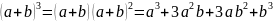 ,那么使用同样的方法,是否还能准确快速地展开
,那么使用同样的方法,是否还能准确快速地展开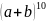 呢?
呢?
学生:不能。
教师:这就需要我们使用新的方法去寻找规律解决问题。那你应该从哪里开始寻找规律;另外,快速展开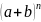 需要我们解决哪些问题?请同学们分组讨论,教师巡视指导。
需要我们解决哪些问题?请同学们分组讨论,教师巡视指导。
学生:从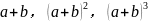 的展开式中寻找规律,要研究展开后有多少项,每一项是什么。
的展开式中寻找规律,要研究展开后有多少项,每一项是什么。
教师:回答的非常好,无论展示的式子多么复杂,我们要研究的最关键点就是多少项,每一项是什么,以及每一项的系数这些规律。请同学们观察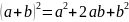 ,一共有多少项?
,一共有多少项?
学生:3项。
教师:3项是在合并之后有三项,那么在没有合并时有几项呢?
学生:4项。
教师:为什么?如何用我们之前学过的知识来说明这个问题。
学生:……
教师: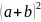 相当于两个
相当于两个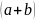 相乘,每个括号里面要出一个字母,然后两个字母相乘,是这样的吗?那大家看一下,
相乘,每个括号里面要出一个字母,然后两个字母相乘,是这样的吗?那大家看一下,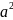 是怎样构成的,
是怎样构成的,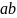 怎样构成的,
怎样构成的,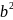 呢?
呢?
学生:都出一个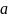 ;一个出
;一个出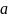 ,一个出
,一个出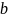 ;都出一个
;都出一个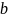 。
。
教师:我们展开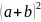 ,要写出某一项,我们需要分几步?两步吧,两个括号相乘,从第一个括号里面拿出一个字母,再从第二个括号里面拿出一个字母,让这两个字母相乘,也就是说在一个括号里面有两种选择,因为在一个括号里面有两个字母,因此在合并之前有2*2=4个项数。合并之后是几项啊?
,要写出某一项,我们需要分几步?两步吧,两个括号相乘,从第一个括号里面拿出一个字母,再从第二个括号里面拿出一个字母,让这两个字母相乘,也就是说在一个括号里面有两种选择,因为在一个括号里面有两个字母,因此在合并之前有2*2=4个项数。合并之后是几项啊?
学生:两步,两种,4项,3项。
教师:那么请大家观察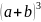 这个三次式,思考在合并之前有几项呢?首先看是不是有三个
这个三次式,思考在合并之前有几项呢?首先看是不是有三个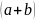 相乘,每个括号里面有两个字母,也就是是说有两种选择吧,因此项数就等于2*2*2=8啊,也就是说展开未合并之前是8项。合并之后是几项?
相乘,每个括号里面有两个字母,也就是是说有两种选择吧,因此项数就等于2*2*2=8啊,也就是说展开未合并之前是8项。合并之后是几项?
学生:8;是;4。
教师:我们观察二次方有3项,三次方有4项,似乎能在这两个展开式中找到了一些规律,3项和4项是不是项数的问题,我们再来看二次方展开每一项都是二次式,三次方展开每一项都是三次式,这又是一个特点,大家再来看一下系数的特点,观察一下,有没有明显的特点。
学生:是,对称。
教师:二次方展开的系数是121,三次方展开的系数是1331。(教师用手指示),那么也就是首项和末项的系数相同对吧,最近大家学了什么内容与这个特点具有类似的地方呢?(强调系数相等,前面的知识点,组合),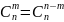 。教师指出二次方展开式的系数分别可以看成
。教师指出二次方展开式的系数分别可以看成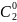 ,
,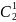 ,
,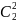 。三次方展示式的系数可以分别看成
。三次方展示式的系数可以分别看成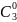 ,
,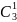 ,
,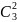 ,
,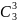 。
。
学生:组合。
教师:展示四次方的展开式,可以看成四个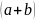 相乘,那么展开后每一项都是四次式,那么根据刚才我们发现的规律,请学生代表回答填空。
相乘,那么展开后每一项都是四次式,那么根据刚才我们发现的规律,请学生代表回答填空。
学生:回答,分别是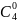 ,
,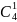 ,
,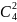 ,
,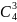 ,
,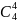 。
。
教师:根据以上的观察、分析,我们能不能猜想出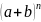 的展开式,请同学们独立动手写下来。
的展开式,请同学们独立动手写下来。
学生:独立书写。
教师:派学生代表进行回答,教师板演二项式定理内容。教师强调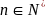 。这个式子就是我们今天学习的二项式定理。
。这个式子就是我们今天学习的二项式定理。
学生:回答。
二、定理的证明
教师:我们刚才都是猜想的过程,数学是一门严谨的学科,这个定理需要我们去证明它,我们需要哪些方面去证明它,项数和系数。N次方是不是相当于n个括号相乘,展示式的每一项是不是相当于从n个括号里面的每个括号选取一个字母,然后相乘,因此它的每一项的项的形式都是几次项?将这些项按a的降幂或a的升幂排列的话,大家看一下,会不会出现PPT上的这些项。之后,我们还需要解决一个什么问题啊,系数,系数的问题可以用我们前面学习的什么样的知识来解决呢?大家看一下对于一般项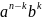 这一项的系数应该是多少呢?根据我们刚才的分析,是不是相当于在n个括号里面选取k个括号出b,然后剩余的n-k个括号里面出a啊,因此
这一项的系数应该是多少呢?根据我们刚才的分析,是不是相当于在n个括号里面选取k个括号出b,然后剩余的n-k个括号里面出a啊,因此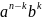 的系数也就是
的系数也就是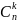 。第一项的系数是
。第一项的系数是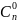 ,它代表着n个括号都没选b,都出a。大家看一下其他项的系数分别是什么。那么这两点项数和系数说明了,我们就能够证明二项式定理。(师生互动,得出结论)
,它代表着n个括号都没选b,都出a。大家看一下其他项的系数分别是什么。那么这两点项数和系数说明了,我们就能够证明二项式定理。(师生互动,得出结论)
学生:回答。
评析
二项式定理是计数原理一章中最为重要的内容之一,它是在学生掌握了基本计数原理和排列与组合的基础上学习的。二项式定理的教学目标是能用多项式运算法则和计数原理证明二项式定理,会用二项式定理解决与二项展开式有关的简单问题。[1]案例中该老师的教学基本实现了本节课的教学目标,教学过程新颖独到,以下是对该教师课堂教学的评析。
该案例展示的教学片断设计整体思路合理,符号定理教学的过程要求,包括定理的引入,定理的证明过程。首先以学生熟悉的
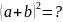 ,
,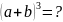 引发学生思考,归纳得出二项式定理公式及特征。然后以数学的严谨性为出发点,引导学生应用组合知识证明定理。教学中,该教师关注学生主体地位,引导学生发现,猜想,探究,归纳,类比,证明,充分培养发现问题、提出问题、分析问题,解决问题的能力,符合《课程标准》的要求。
引发学生思考,归纳得出二项式定理公式及特征。然后以数学的严谨性为出发点,引导学生应用组合知识证明定理。教学中,该教师关注学生主体地位,引导学生发现,猜想,探究,归纳,类比,证明,充分培养发现问题、提出问题、分析问题,解决问题的能力,符合《课程标准》的要求。
选择学生熟悉的问题情境是该案例的亮点,巧妙地将现实生活的问题与二项式定理联系起来,造成学生认知冲突,激发学习兴趣,激励学生学习二项式定理,体会数学和现实生活的联系,这样的导入后才有师生互动、生生互动,生动活泼的教学氛围。这样的设计独具匠心、引人入胜,能够取得较好的教学效率和教学效果,使得教师组织者、引导者和合作者的身份和学生的主体性地位都得以体现[2]。
该案例也存在不足之处,虽然学生经历了探究二项式定理的过程,但是教师在课堂中缺乏对学生做题的易错点的点拨,比如在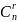 中r的取值范围,教师在课堂教学中并未着重强调这一点,学生就不能很好意识到
中r的取值范围,教师在课堂教学中并未着重强调这一点,学生就不能很好意识到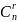 中r的取值范围。因此可以加以改进,按照教材的顺序,对语言进行精炼,充分体现定理的形成发展过程,抓住教材上关注的没一点,重视
中r的取值范围。因此可以加以改进,按照教材的顺序,对语言进行精炼,充分体现定理的形成发展过程,抓住教材上关注的没一点,重视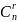 中r的取值范围。
中r的取值范围。
参考文献
1中华人民共和国教育部制定.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.
2王美春.学习共同体中的教师角色[J].黑龙江教师发展学院学报,2020, No.267,32-34.