基于提升算法的3阶Daubechies离散小波变换的FPGA实现

基于提升算法的 3阶 Daubechies离散小波变换的 FPGA实现

张宝贵，周俊

中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443003

摘 要：为进一步提高小波变换的计算效率，研究基于提升算法的3阶Daubechies离散小波变换及其逆变换的FPGA实现。简要介绍提升算法的基本原理，给出3阶Daubechies小波变换及其逆变换的提升算法过程，对正变换与逆变换的硬件实现结构进行设计。该结构无需附加内存，且采用流水线技术实现小波系数的快速并行输出，大大节省了传统变换所需的存储空间并提高了计算速度。在Quartus设计软件中对提升算法结构进行仿真，验证了提升结构的正确性。分别使用传统的基于卷积的DB3小波滤波器和设计的DB3提升结构对包含噪声的模拟信号进行小波阈值滤波处理。结果表明：提升结构算法计算复杂度小，在可承受的信噪比范围内，能够快速实现信号的小波变换处理。

关键词： 提升算法；DB3小波；小波变换；FPGA实现

小波变换是20世纪80年代后期发展起来的应¹用数学分支，并在近十几年里得到了快速的发展，由于其具有良好的时频局部特性和多分辨分析特性，小波变换在语音识别、图像处理、信号去噪、数据压缩、特征分析等领域都有广泛的应用^[1-3]。长期以来，离散小波变换的工程实现一直使用Mallat快速算法^[4]。这种基于卷积的算法计算复杂，运算量大，对存储空间的要求高，不太利于硬件的实时实现，制约了它在速度较高或数据量较大的信号处理场合的应用。

Daubechies等人在上世纪90年代末提出了小波变换的提升算法^[5]，被誉为第2代小波变换。它既继承了第1代小波良好的时频局部特性和多分辨分析特性，又不依赖于傅立叶变换，因此计算速度快，计算时无需额外的存储开销，非常适合硬件实现。目前使用提升算法的离散小波变换硬件设计研究都集中于JPEG标准中的5-3小波和9-7小波上^[6-7]，以完成二维图像的实时处理。对于信号处理中其他常用的小波变换研究较少，因此，笔者研究基于提升算法的3阶Daubechies小波变换和逆变换的硬件实现，以方便其在高速信号处理或实时图像处理等领域的应用。

1 提升算法的基本原理

Daubechies在文献[5]中提出了小波变换的提升算法，并且证明了任何离散小波变换都可以被分解成为一系列简单的提升步骤，可以用提升算法来实现。提升算法中的离散小波变换是通过将小波滤波器的多相矩阵(polyphase matrix)分解成为一系列的上三角阵、下三角阵和一个对角阵来实现的。多相矩阵P(z)可以使用Euclidean算法进行分解得到式(1)，此即为小波变换的提升方案。一个提升方案可以划分成分解、预测、更新和缩放4个步骤，图1是提升算法前3个主要步骤示意图。

(1)

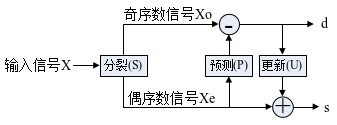
图1 提升算法示意图

分解：通常将输入信号分为偶数序列和奇数序列。预测：在基于原始数据相关性的基础上，用偶数序列X_e与一个预测算子P去预测奇数序列X_O，然后使用预测值与奇数序列的差值来代替奇数序列，即d=X_O-P(X_e)。这样就能使用更小的子集来代替原始信号集。更新：为了使原始信号的某些全局特性在偶序数信号中继续保持，需要进行更新。可以利用第二步计算得到的d进行更新，构造一个算子U去更新偶序数信号，s=X_e+U(d)。d和s代表最终输出的高频和低频信号。可以看出，提升算法能够在计算过程中不需要除了前级步骤的输出之外的数据，即实现原位运算。这样在每个点都可以用新的数据流替换旧的数据流，大大节省了运算过程中间变量的存储空间。

2 DB3离散小波变换的提升算法

Daubechies在文献[8]中给出了DB3小波变换的低通和高通滤波器，分别为：

(2) (3)

式中各系数为：h_-2=0.333, h_-1=0.807, h₀=0.459, h₁=-0.135, h₂=-0.085, h₃=0.035。设P(z)是DB3小波正变换的多相矩阵，笔者使用Euclidean算法对P(z)进行分解，转化为一系列的上三角阵、下三角阵和一个对角阵相乘的形式，得到式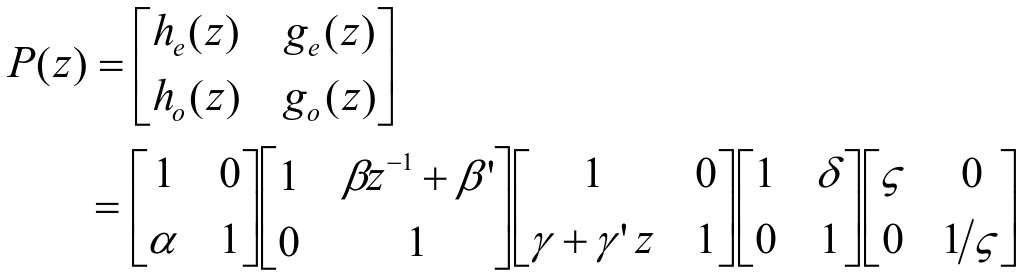(4)：

(4)

式中各系数为：α ≈ -0.4123, β ≈ -1.5651, β' ≈ 0.3524, γ ≈ 0.0285, γ' ≈ 0.4922, δ ≈-0.3896, ς ≈ 1.9182。将输入信号数据x_n分解为偶数序列信号x_2n和奇数序列信号x_2n+1，DB3小波正变换就可以转化为以下步骤：

(5)

(6)

(7)

(8)

(9)

(10)

式中s'_n、d'_n、s''_n、d'都是提升算法的中间结果，s_n和d_n分别为输出的低频系数和高频系数。由于式(6)中出现了s'_n前一时刻的信号s'_n-1，这里将式(6)～(10)中信号都延迟一个时刻，改写为：

(11) (12) (13) (14) (15)

根据式(4)还可以得到DB3小波逆变换的滤波器组的多相矩阵P(z)^-1，式中各系数的值与式(4)中相同，小波逆变换也可类似地转化为一系列乘法与加法运算，这里不再赘述。

（16）

3 基于提升算法的离散小波变换FPGA实现

3.1 DB3离散小波变换与逆变换的硬件结构

根据上述的提升算法计算步骤，设计了DB3小波变换与逆变换的硬件实现结构，如图2和图3所示。图2中“pider”表示信号分解器，将信号分解为奇偶序列；“mixer”是信号合成器，将输入的两路信号按奇偶秩序合成为一个信号；“P”是寄存器，表示信号延迟一个时间单位；“+”和“×”分别表示加法器和乘法器，乘法器的系数值就是提升算法计算步骤公式中的系数值。根据设计的小波变换与逆变换硬件实现结构，就能够方便地在FPGA中构建DB3小波变换与逆变换的功能模块。

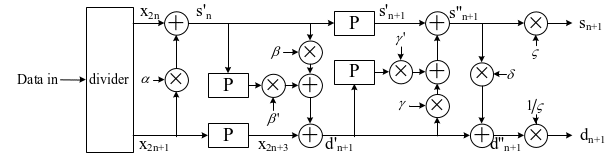
图2 DB3小波变换硬件实现结构

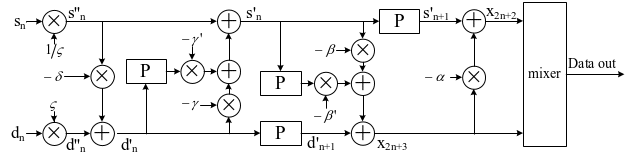
图3 DB3小波逆变换硬件实现结构

3.2 DB3离散小波变换与逆变换的FPGA设计

现场可编程门阵列(field programmable gate array，FPGA)是近年来广泛应用的超大规模、超高速的可编程逻辑器件，由于其具有高集成度、低功耗、高运算速度等优点，在超高速信号处理方面有非常广泛的应用。笔者使用Altera公司的Cyclone系列FPGA来实现DB3离散小波变换，FPGA型号为EP2C8Q208C8，使用Altera公司的Quartus II软件进行FPGA功能设计。首先在原理图设计模式下构建DB3小波变换的各步骤运算模块，它们分别对应式(5)～(15)。对各步骤运算模块创建各自设计文件，使用VHDL语言进行模块的功能描述。分别将前一步模块的输出作为后一步模块的输入，各模块使用统一系统时钟信号，连接各模块之后构成DB3离散小波变换与逆变换的整体模块。

3.3 软件仿真

在Quartus II软件中完成设计后，对工程文件进行编译，并建立矢量波形文件进行仿真测试，在仿真波形文件中添加输入信号、输出信号和各级运算模块中的寄存器以检验提升算法各步骤的运算结果。生成Quartus仿真网表后进行系统工程仿真。输入信号使用常见的正弦信号。通过对比得到的仿真结果和式(5)～(15)的公式的计算结果，可以验证设计的工程文件实现了DB3离散小波正变换和逆变换。但是各级运算步骤的中间量存在微小的误差，这主要是由于使用FPGA进行乘法除法运算时都是采用二进制数据移位的方式进行的，因此对滤波器系数有略微的近似。另外，提升算法每一步骤模块执行都会延时一个时钟周期，这是因为FPGA内部寄存器之间的赋值需要在下一个周期时钟上升沿才能触发完成。将正变换得到的输出结果(即高频输出信号和低频输出信号)作为逆变换的输入信号进行仿真验算，将结果对比原始输入的信号发现丢失了末尾几个数据，这是由于在提升算法步骤中，有部分公式需要将此时刻s值与下一时刻d值共同计算，这使最后的一个s值要作舍去处理，经过正变换与逆变换2次提升算法，就会丢失几个数据。但这对于数据量较大的输入信号的影响可以忽略不计。

4 小波阈值去噪与结果分析

滤波去噪是小波变换的一个重要应用领域，D.L.Donoho和I.M.Johnstone在小波变换的基础上提出了小波阈值去噪的概念，该方法在信号处理方面得到了广泛的应用。Donoho提出的小波阈值去噪方法分为以下3个步骤：

1) 对输入信号作小波变换，得到一组小波系数；

2) 对小波系数进行阈值处理，得到修正后的系数值；

3) 利用修正后的系数值进行小波逆变换，重构信号作为滤波去噪后的信号。

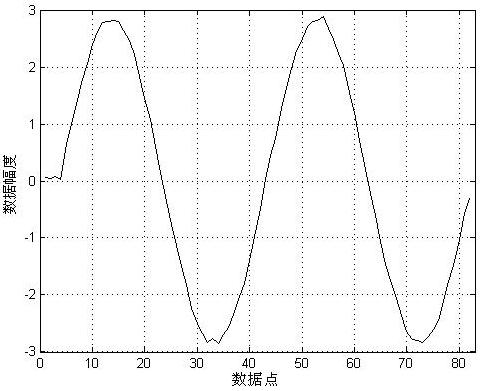
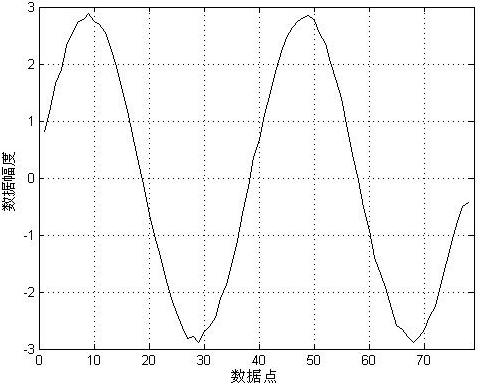
第二步的阈值处理是小波阈值去噪的重要步骤。Donoho小波阈值处理的基本思想是：当小波系数小于某个临界阈值时，认为这时的小波系数主要是由噪声引起的，予以舍弃；当小波系数大于这个临界阈值时，认为这时的小波系数主要是由信号引起，但仍含有噪声的影响，于是把这一部分系数进行压缩保留，即软阈值方法。为了验证本文中小波提升结构的实际应用有效性，这里将提升算法应用于小波阈值去噪的验算。在正弦波中添加高斯噪声构成输入信号，原始信号与输入信号如图4所示。

分别使用本文中的提升结构和传统的基于卷积的3阶Daubechies滤波器完成该信号的3层小波变换，得到的结果如图5所示。图5中左侧为基于卷积DB3小波分解得到的系数，右侧是基于提升方案的DB3小波分解得到的系数。

从图中的结果曲线可以看出小波变换后得到的高频系数主要是噪声引起的，低频系数则包含了原信号的信息。虽然两种方法得到的高频系数存在差异，但对高频系数进行阈值处理后，高频系数都被置零，而两种方法得到的低频系数基本相同。再进行信号的小波重构，得到结果如图6所示。

可以看出两种小波阈值去噪方法都有效去除了原输入信号中的噪声，但是使用提升小波实现信号滤波的结果中出现了信号头部的畸变，这主

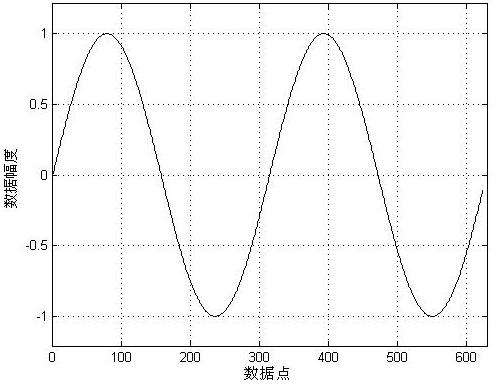
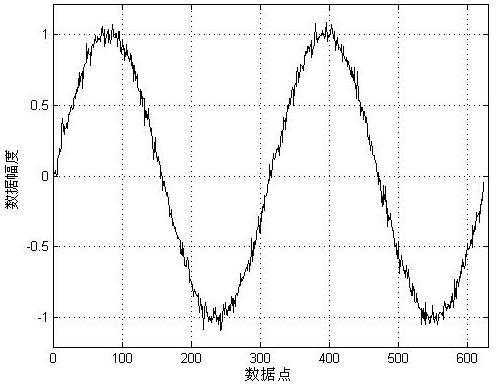
(a) 原始验算信号 (b) 添加噪声的信号

图4 原始信号与添加噪声后的信号

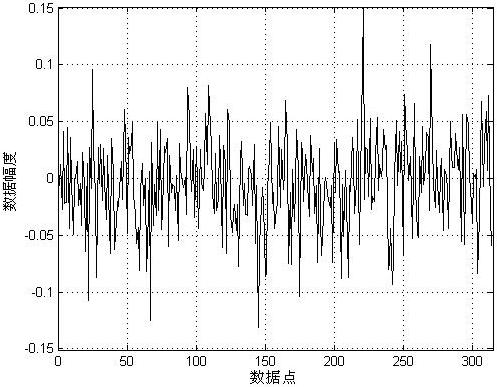
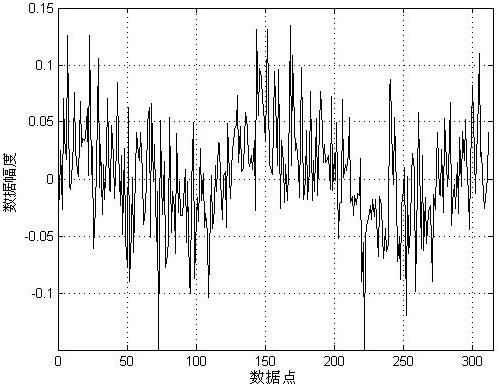
(a) 1层DB3小波分解与提升小波分解得到的高频系数

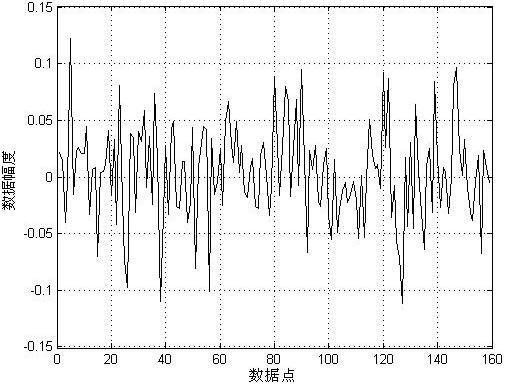
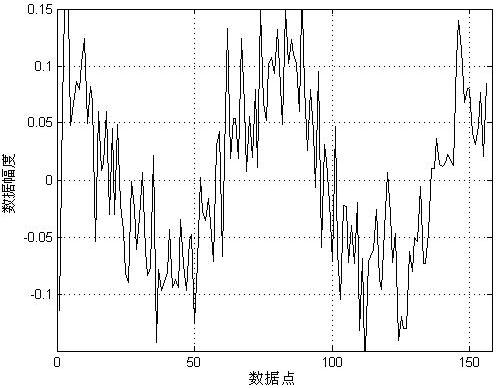
(b) 2层DB3小波分解与提升小波分解得到的高频系数

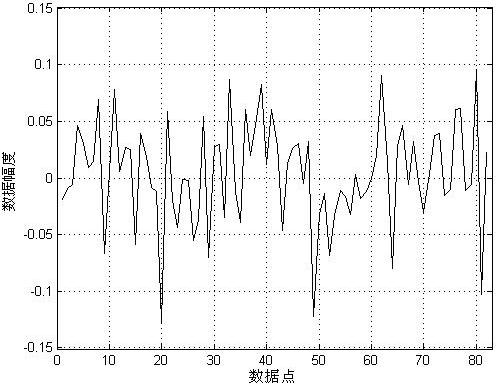
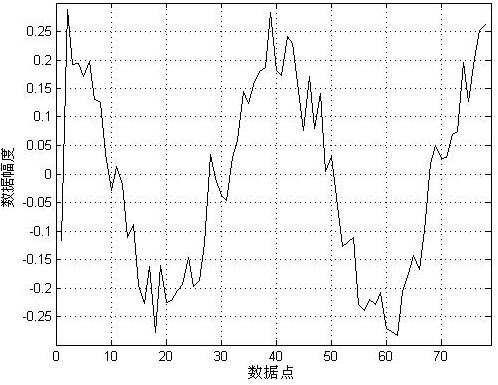
(c) 3层DB3小波分解与提升小波分解得到的高频系数

(d) 3层DB3小波分解与提升小波分解得到的低频系数

图5 三层DB3小波变换的结果

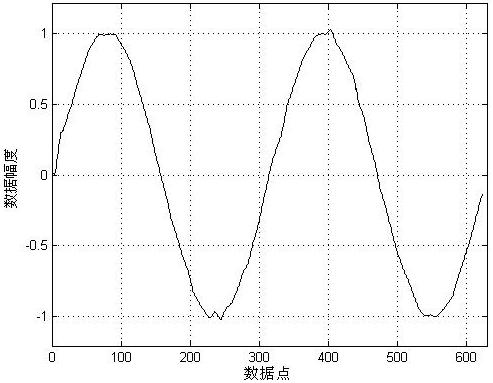
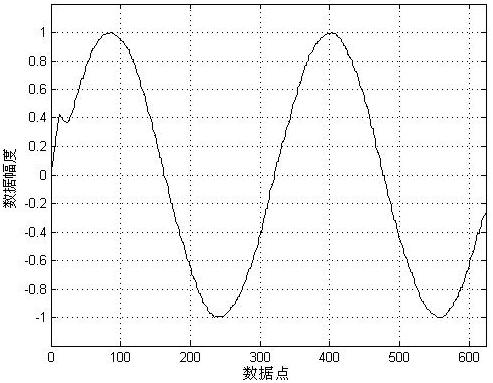
图6 小波阈值去噪处理的结果

要还是由前述的提升算法中首尾信号丢失造成的，对于信号数据量大的情况，这种影响可以忽略，而在数据量小的情况下要克服这一不足，可以使用信号的补零延拓或对称延拓等方法。为了对两种方法进行定量比较，笔者使用均方误差(MSE)和信噪比(SNR)作为比较指标，它们的定义如下：

(17)

(18)

式中s为原始正弦信号；y为含噪信号经过滤波处理后的输出信号；N为信号数据的长度。将输出的两种滤波处理后的信号和原始正弦信号分别代入式(17)和式(18)，计算得到基于卷积的DB3小波阈值处理结果的均方误差为2.6337×10^-4，信噪比为75.5565 dB，而基于提升小波的阈值去噪处理结果的均方误差为6.4×10^-3，信噪比为43.588 8 dB。虽然使用提升小波实现阈值去噪的结果的两个性能指标都较基于卷积的处理结果略低，但是仍在可接受的范围之内，信号波形没有产生严重畸变，能够应用于信号或图像的滤波去噪实时硬件实现。

5 结束语

笔者研究了基于提升算法的3阶Daubechies离散小波变换及其逆变换的硬件实现。由于提升结构能实现小波变换的流水线快速实现，计算复杂度小，可以达到实时处理的程度。实例计算和结果对比分析证明了笔者设计的硬件结构的可行性和实用性。

参考文献

[1] 陈晓惠, 郑晨, 段汕. 形态小波域多尺度马尔可夫

模型在纹理图像分割中的应用[J]. 中国图像图形学

报,2011, 16(5): 761-766.

[2] 姚诚, 刘广孚, 李忠国. 基于小波系数功率谱的潜

油电泵偏磨故障诊断[J]. 仪器仪表学报, 2011, 32(8):

1757-1762.

[3] 袁飞. 基于平移不变小波的语音信号去噪研究[J].

自动化技术与应用, 2011, 30(8): 40-42.

[4] Mallat S G. A theory for multiresolution signal

decomposition: the wavelet representation[J]. IEEE

Transactions on Pattern Analysis and Machine

Intelligence, 1989, 11(7): 674-693.

[5] Daubechies I, Sweldens W. Factoring wavelet

transforms into lifting steps[J]. Journal of Fourier

Analysis and Applications, 1998, 4(3): 247-269.

[6] 郝燕玲, 刘营. 应用于JPEG2000 的离散小波变换并

行超大规模集成结构[J]. 光学精密工程, 2009, 7(5):

1181-1186.

[7] 王前, 吕东强, 栗靖. 新型9/7小波基构造及快速实

现[J]. 电子与信息学报, 2009, 31(5): 1210-1213.

[8] Daubechies I. Orthonormal bases of compactly

supported wavelets[J]. Comm. Pure Appl. Math., 1988,

41(6): 909-996.

1

6