山西省长治市上党区第一中学校, 047100
笔者近日在教学人教A版高中数学必修二《第三章 直线方程》内容时,给学生列举了这样一道试题:
过点P(1,2)的直线l与x轴的正半轴、y轴的正半轴分别交于A,B两点,当∆AOB的面积最小时,求直线l的方程。
同学们主要有以下几种解法:
解法1:由题意知,直线l斜率存在。
设直线l的方程为:y-2=k(x-1)(k<0),则A(1- 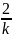 ,0),B(0,2-k),
,0),B(0,2-k),
所以 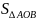 =
=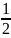 OA∙OB
OA∙OB
=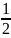 |1-
|1- 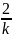 |∙|2-k |
|∙|2-k |
=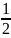 |-k+
|-k+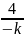 +4|
+4|
≥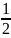 |2
|2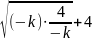 |=4,
|=4,
当且仅当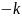 =
=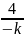 ,即k=-2时取等号。
,即k=-2时取等号。
∴∆AOB的面积的最小值为4,此时直线l的方程为
y-2=-2(x-1),即2x+y-4=0。
思路小结:本解法通过设出直线的点斜式方程,将面积表示为关于斜率k的函数,通过研究函数的最小值进而得到围成三角形面积的最小值。
解法2: 由题意,设直线l的方程为: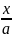 +
+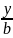 =1(a>1,b>2),
=1(a>1,b>2),
∵点P(1,2)在直线l上,∴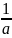 +
+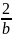 =1。
=1。
由基本不等式,得1= 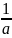 +
+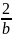 ≥2
≥2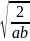 ,即ab≥8,
,即ab≥8,
于是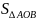 =
=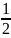 ab≥4,当且仅当
ab≥4,当且仅当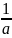 =
=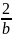 ,即a=2,b=4时取等号。
,即a=2,b=4时取等号。
∴∆AOB的面积的最小值为4,此时直线l的方程为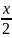 +
+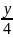 =1,即2x+y-4=0。
=1,即2x+y-4=0。
思路小结:本解法通过设出直线的截距式方程,然后构建出基本不等式对围成三角形面积的最值进行求解。
解法3:同解法2,得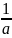 +
+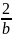 =1。由于a>0,b>0,令
=1。由于a>0,b>0,令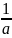 =
=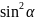 ,
,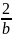 =
=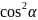 ,则a=
,则a=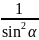 ,b=
,b=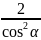 ,于是
,于是
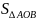 =
=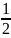 ab=
ab=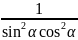 =
=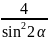 。
。
∵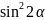 ≤1,∴
≤1,∴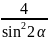 ≥4,即
≥4,即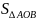 ≥4,
≥4,
当且仅当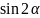 =±1,即α=
=±1,即α=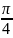 +
+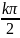 ,k∈Z时取等号,此时a=2,b=4。
,k∈Z时取等号,此时a=2,b=4。
∴∆AOB的面积的最小值为4,此时直线l的方程为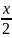 +
+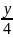 =1,即2x+y-4=0。
=1,即2x+y-4=0。
思路小结:本解法根据直线截距式方程的特点,类比三角函数的平方关系,通过三角代换,结合三角函数的有界性,对围成三角形面积的最小值进行了求解。
解法4:如图1所示,过点P分别作x轴、y轴的垂线,PM,PN,垂足分别为M,N。设
θ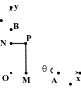 =∠PAM=∠BPN,0<θ<
=∠PAM=∠BPN,0<θ<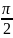 。于是
。于是
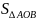 =
=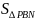 +
+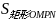 +
+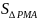 =
=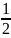 ╳1╳tanθ+2+
╳1╳tanθ+2+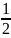 ╳2╳
╳2╳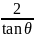
=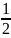 tanθ+
tanθ+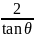 +2
+2
≥2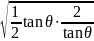 +2=4,
+2=4,
(图1)
当且仅当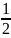 tanθ=
tanθ=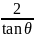 ,即tanθ=2时取等号。此时直线l的斜率为-2。
,即tanθ=2时取等号。此时直线l的斜率为-2。
∴∆AOB的面积的最小值为4,此时直线l的方程为y-2=-2(x-1),即2x+y-4=0。
思路小结:本解法通过观察图形的特点,进行了面积分割,以角度为自变量,进行了面积最小值的求解。
做完此题之后,我们不妨对此类问题的一般情形进一步探究如下:
问题 1 在一般情况下,过任意一点P(m,n)(其中m>0,n>0)的一条直线与x、y轴正半轴交于A,B两点时,所围成的∆OAB面积最小值怎么求解?此时,最小面积又是多少?
针对该问题,我们从以上解法2,可以找到其中的答案,求解过程如下:
解: 由题意,设直线l的方程为: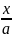 +
+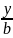 =1(a>m,b>n),
=1(a>m,b>n),
∵点P(m,n)在直线l上,∴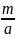 +
+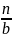 =1。
=1。
由基本不等式,得1 = 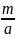 +
+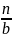 ≥2
≥2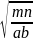 ,即ab≥4mn,
,即ab≥4mn,
于是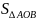 =
=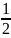 ab≥2mn,当且仅当
ab≥2mn,当且仅当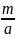 =
=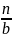 ,即a=2m,b=2n时取等号。
,即a=2m,b=2n时取等号。
∴∆AOB面积的最小值为2mn,此时直线l的方程为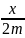 +
+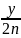 =1,即nx+my-2mn=0。
=1,即nx+my-2mn=0。
由以上解答,我们找出了此题的一般性结论,培养了学生从特殊到一般的数学思想方法。
利用坐标法解决解析几何问题,主要体现了数形结合思想。对于本题,我们可以思考以下问题。
问题 2 当所围成的三角形面积取得最小值时,此时相应的图形有何几何特征呢?
由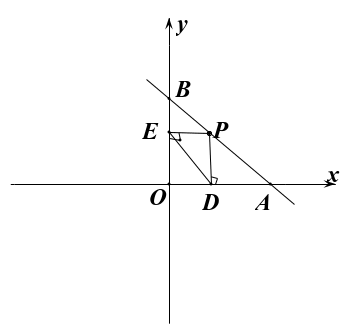 以上代数解法,我们发现∆AOB面积取得最小值时的条件,也就是基本不等式等号成立的条件:
以上代数解法,我们发现∆AOB面积取得最小值时的条件,也就是基本不等式等号成立的条件: 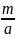 =
=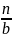 ,我们可以将该等式等价变形如下:
,我们可以将该等式等价变形如下: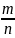 =
=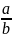 。那么变形以后的等式说明了什么问题呢?从右图2中,我们不难找到答案所在。
。那么变形以后的等式说明了什么问题呢?从右图2中,我们不难找到答案所在。
过P点分别作PD⊥x轴,PE⊥y轴,连接DE。 (图2)
由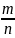 =
=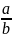 可知:
可知: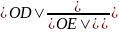 =
=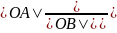
故从图2中,我们可以得到:Rt∆ODE∽Rt∆OAB,
即此时,DE//AB,
所以我们可以得到以下结论:
结论I:过任意一点P(m,n)(其中m>0,n>0)的一条直线与x、y轴正半轴交于A,B两点时,所围成的∆OAB面积最小值为2mn;
结论II:前提条件同上,当围成∆OAB面积最小时,DE//AB,此时我们可以很容易得到直线AB的斜率为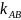 =
=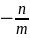 ,进而由点斜式整理化简,我们可以得到直线AB的方程形式为:nx+my-2mn=0;
,进而由点斜式整理化简,我们可以得到直线AB的方程形式为:nx+my-2mn=0;
结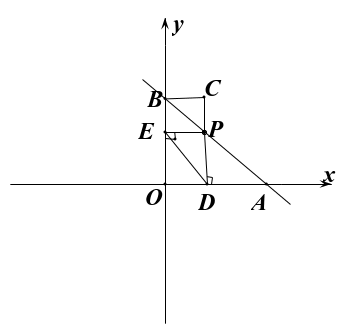 论III:前提条件同上,当围成∆OAB面积最小时,过点B作BC⊥y轴,延长DP与BC相交于点C。有以下结论成立:
论III:前提条件同上,当围成∆OAB面积最小时,过点B作BC⊥y轴,延长DP与BC相交于点C。有以下结论成立:
①四边形BEPC为矩形,由结论II可知,四边形BEDP此时为平行四边形,所以,∆CBP、∆BEP、∆EPD面积相等,都等于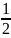 mn;
mn;
②此时矩形BODC的面积为2mn,和∆OAB的最小面积是相等的; (图3)
③此时DE为∆OAB的中位线,∆CBP、∆PDA面积相等,都等于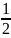 mn。
mn。
加强对数学问题的探究,有助于帮助学生在跳出题海的同时对所学的知识融会贯通,从而减轻学生的学习压力,在奇妙的探究过程中,让学生领略数学的魅力、体会学习数学的兴趣。
参考文献:
[1] 潘振嵘.摭谈对教材例、习题功能的深层挖掘 [J].数学通讯(下半月),2015(5).
[2] 谢宗明. 解析直线与坐标轴围成的三角形面积问题[J]. 中学生数理化(教与学), 2010(11).
[3] 杨绍国, 董成勇. 过定点直线与坐标轴围成的三角形问题探究[J]. 数学通讯, 2015(Z4).