基于动态自适应粒子群算法的加热炉钢温模型的研究

基于动态自适应粒子群算法的加热炉钢温模型的研究

王亚军

（淮北安兴古镇文化旅游开发有限责任公司，安徽淮北 235099）

摘要：蓄热步进梁式加热炉是轧钢生产线上非常重要的热工设备，针对钢坯的加热过程具有大滞后、大惯性、多变量、强耦合、时变、非线性等特点，传统的机理模型不够灵活，计算复杂，假设条件过多，因此，本文以蓄热步进梁式加热炉为研究对象，开展预测模型的研究工作。在标准粒子群算法的基础上进行了动态自适应调整惯性权重和学习因子的改进，经仿真验证，用该改进粒子群算法优化后，模型的收敛速度和预测精度有了进一步的提高。

关键词：加热炉；钢温预测模型；神经网络；粒子群

1 引言

蓄热步进梁式加热炉是轧钢生产线上非常重要的热工设备，由于目前的检测技术和加热炉自身因素等条件限制，使得直接、准确测得加热过程中的钢坯温度分布还有很大困难，只有钢坯出炉后才能知道出钢温度是否合格，一旦不合格也很难回炉补救了，因此建立加热炉的钢温预测模型，对于改善钢坯的加热质量是十分必要的。钢坯的加热过程具有大滞后、大惯性、多变量、强耦合、时变、非线性等特点，传统的机理模型不够灵活，计算复杂，假设条件过多。

粒子群算法是一种基于群智能方法的演化计算技术，同遗传算法类似，是基于迭代的优化工具，但它不像遗传算法那样要对个体进行选择、交叉和变异的操作，它采用速度–位移的模式，其收敛速度快（尤其是在进化初始阶段）、鲁棒性较高、全局搜索能力强，而且不需借助问题本身的特征信息（如梯度等），操作简单、易于编程且功能强大，是很好的优化工具。目前，已经提出了多种PSO的改进算法，也被广泛应用于函数优化、神经网络的训练、模式分类、模糊系统控制等不同领域。PSO的优点在于不仅简单容易实现，又有深刻的智能背景，它既适合于作科学研究，又特别适合于工程应用。本文在研究大量的文献资料，并做了大量的仿真试验，同时考虑所建模型实际的应用背景的基础上，提出了一种动态自适应调整粒子群参数的改进策略，能根据粒子群每代搜索的实际情况自适应的调整惯性权重和学习因子等主要参数，并引入了种群收敛程度判别机制，显著的提高了搜索的速度和精度。

2 粒子群算法的改进策略

粒子群算法的改进有多种方式，主要有：将基本PSO算法和选择机制相结合可得到杂交PSO模型（Hybrid PSO，HPSO），与一般的PSO及GA算法相比，HPSO收敛速度快，搜索精度高，对一些非线性优化问题可以得到较满意的结果；免疫PSO模型将免疫系统的免疫信息处理机制（如多样性、免疫记忆、免疫自我调节等）引入到粒子群算法中，这种模型结合了粒子群优化算法的全局搜索能力和免疫系统的免疫信息处理机制，从而可有效避免粒子群算法易于陷入局部极值点的缺点，提高了进化后期算法的收敛速度和精度；在PSO算法的搜索过程中，随着迭代次数的增加，搜索区域会越来越小，所以自适应PSO算法比标准PSO收敛速度更快，结果更好；基于遗传算法的PSO模型，将遗传进化机制引入到微粒群进化过程中，即在粒子群更新过程中，引入杂交和变异机制，该算法也可看作是对杂交粒子群的扩展与深入；基于模拟退火的PSO模型，利用模拟退火算法较强的跳出局部最优解的能力，将其与PSO算法的全局寻优能力，以及计算速度快、实现简单、需要调整的参数少等优点相结合，从而避免了PSO容易陷入局部极值点的缺点，提高了PSO进化后期的收敛速度。两者的结合在许多优化问题上都取得了很好的效果，显著的提高了搜索的精度，具体广阔的应用前景。

3 实现步骤

本文在研究大量的文献资料，并做了大量的仿真试验，同时考虑所建模型实际的应用背景的基础上，提出了一种动态自适应调整粒子群参数的改进策略，能根据粒子群每代搜索的实际情况自适应的调整惯性权重和学习因子等主要参数，并引入了种群收敛程度判别机制，显著的提高了搜索的速度和精度，现具体叙述如何应用该算法优化钢温模型。

3.1 粒子群算法早熟收敛分析

本文用来评价粒子群早熟收敛程度的指标定义如下：

设种群的粒子总数为 ，第 次迭代中粒子 的适应度值为 ，最优粒子的适应度值为 ；粒子群的平均适应度值为 ，将适应度值优于 的粒子的适应度求平均得到 ，定义 ， 可用来评价粒子群的早熟收敛程度，且 越小说明粒子群越趋向于早熟收敛。

分析式（4.3）可以发现，粒子群到达局部最优附近时，粒子速度的更新主要由 决定。由于标准PSO算法的惯性权重 通常小于1，粒子的速度将会越来越小，甚至停止运动，发生早熟收敛。如果发生这种情况，本文的改进算法可赋予粒子大于1的惯性权重，以使粒子具有较大的速度，从而有效地跳出局部最优，避免早熟收敛。

3.2 自适应调整惯性权重

为了克服标准PSO算法参数设置的不足，应根据粒子群个体的搜索情况和群体早熟收敛程度自适应地调整惯性权重

。本文的自适应调整策略，不仅用到个体的搜索程度和群体早熟收敛等信息，还根据个体适应度的不同将种群分为3个子群，分别采用不同的自适应调整 的操作，使得群体始终保持惯性权重的多样性。惯性权重较小的粒子用来进行局部寻优，加速算法的收敛；惯性权重较大的粒子早期进行全局寻优，后期用来跳出局部最优，避免早熟收敛。这样，具有不同惯性权重的粒子各尽其责，全局寻优和局部寻优同时进行，在保证算法全局收敛和收敛速度之间做了一个很好的折衷。具体做法为，适应度值为 的粒子 ，其惯性权重 调整如下：

（1） 优于

这些粒子为群体中较为优秀的粒子，更容易接近或已经比较接近全局最优，应被赋予较小的惯性权重，以加速向全局最优收敛。本文根据粒子适应度值按下式调整粒子 的惯性权重，其中 为惯性权重的最小值，本文取0.5。粒子越优秀，其惯性权重相应越小，强化了局部寻优。

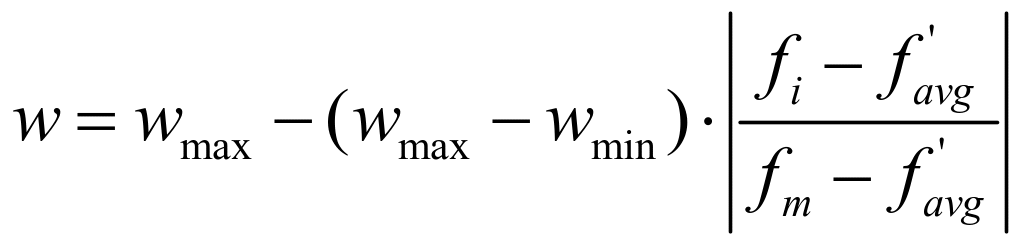（1）

（2） 优于 ，但次于

满足此条件的粒子是群体中的一般粒子，具有良好的全局寻优和局部寻优能力。这里不再采用线性递减 的策略，而是惯性权值 随着搜索的进行按余弦规律减小，开始搜索时 能较长时间保持较大值以提高搜索效率，在搜索后期 能较长时间保持较小值以提高搜索精度，本文 的修正公式为：

（2）

其中： 为搜索开始时最大的 ， 为搜索结束时最小的 ， 为迭代所进行的步数，即粒子搜索的当前代数， 为允许的最大迭代步数。

（3） 次于

满足此条件的粒子是群体中较差的粒子，对其惯性权重的调整引用文献^[45]中调整控制参数的方法：

（3）

算法停滞时，若粒子分布较为分散，则 较大，由上式降低粒子的 ，加强局部寻优，以使群体趋于收敛；若粒子分布较为聚集，如算法陷入局部最优，则 较小，通过上式增加粒子的 ，使粒子具有较强的探查能力，从而有效地跳出局部最优。上式中参数 ， 的选择对算法的性能有很大的影响。 主要用来控制 的上限， 越大， 的上限越大。根据前面分析， 的选取应使上式能够提供大于1的惯性权重。本文取 ，显然 ，主要用来控制上式的调节能力；若 过大，在早期停滞时， 会迅速变得很小，虽然会加快收敛，却使算法在早期的全局寻优能力不足：若 过小，则上式的调节能力不是很明显，尤其在后期算法不能有效地跳出局部最优，本文取 。

3.3自适应调整加速常数

在粒子群优化算法中，加速系数 和 分别控制“认知”部分和“社会”部分对各粒子速度的影响。取 和 分别如下

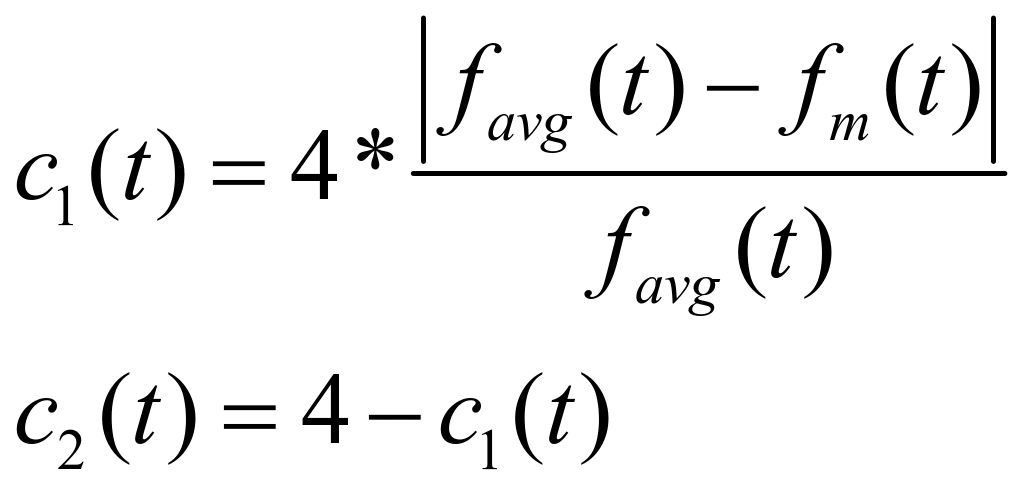（4）

其中， 是粒子群当前代的平均适应度， 是粒子群当前的全局最优位置的适应度。因此：

（5）

3.4粒子群收敛程度的判定

粒子群算法在运行过程中，如果某粒子发现了一个当前最优位置，其它粒子将迅速向该位置靠拢；如果该最优位置是局部最优点，粒子速度会迅速降低，接近为0，此时粒子群就会无法在解空间内继续搜索，因此，算法将陷入局部最优，出现所谓的早熟收敛现象。试验证明，无论是早熟收敛还是全局收敛，粒子群中的粒子都会出现“聚集”现象：要么所有粒子聚集在某一特定的位置，要么聚集在某几个特定位置，这主要取决于问题本身的特性以及适应度函数的选择。

通过考察粒子的适应度方差，和当前全局极值的适应度来确定变异的时机。

当 _（6）

时，说明粒子群搜索陷入了早熟收敛。

式中： ——收敛的精度，它的取值与实际问题有关，一般取一个远小于 的最大值； ——当前全局最优粒子的适应度值； ——粒子适应度的理论最优值或经验最优值。也就是说：当算法收敛而又未获得全局最优解，即陷入早熟收敛时，再继续进行粒子群的搜索已无多大的意义，此时可退出粒子群的循环，经过试验选定 。另外，早熟收敛即为最优值连续数代保持不变，因此当最优值连续数代不变或变化很小时，也应退出粒子群的循环，此方法可作为前种早熟判据的补充。

以动态自适应调整粒子群参数的改进粒子群算法来代替原网络的L-M学习算法去优化三段式神经网络钢温预测模型，以下具体说明改进的自适应粒子群算法优化神经网络的实现过程。实现步骤如下：

（1）建立三个串联的BP神经网络，输入训练数据，即提供输入向量 和期望输出向量 ，并进行归一化处理；

（2）粒子群参数初始化：给定粒子个数 ，初始化每个粒子，包括最大迭代次数及每个粒子的维数，种群允许的最小适应度 （即当搜索到的全局极值点的适应度小于 时，退出循环，不再搜索），惯性权重 ，收敛的精度 ，粒子适应度的理论最优值 ，记录粒子群全局最优值保持不变的代数的参数 ，随机产生粒子的初始位置 和初始速度 ，置迭代次数 ；

（3）根据粒子位置 和训练样本，据实际问题计算每个粒子的适应度；

（4）根据误差函数 ，评价每个粒子的适应度，更新当前的个体极值 和全局极值 ；

（5）根据式（1）、（2）、（3）调整 ，根据式（4）调整学习因子 ；

（6）更新每个粒子的位置（即调整权值和阈值）

和飞行速度 。检验位置和速度是否越出边界，若是，调整它们为算法规定的最大值；

（7）当种群适应度达到最小设定值或达到最大迭代次数，学习过程结束，否则，令 ，返回第（3）步继续迭代，直至满足要求为止；

（8）寻找到的最优粒子的位置即为要优化的神经网络的权阈值，将其赋给神经网络，输入预测数据并进行相应的规范化处理，仿真可得出结果。

4 仿真验证

现采用动态自适应PSO算法代替第三章中用到的L-M算法（利用梯度下降法与高斯-牛顿法结合而形成的快速优化算法）来优化BP神经网络，借此在原标准PSO算法优化的基础上进一步提高三段式加热炉钢温预测模型的预测精度。

经过多次的仿真试验，各项参数的设置为：粒子的个数 ；由于BP网络的结构是5-15-1，所以每个粒子的维数 ；最大迭代次数 ；种群允许的最小适应度 ；惯性权重 ， ；收敛的精度 ，粒子适应度的理论最优值 ，记录粒子群全局最优值保持不变的代数的参数 ；粒子的位置范围是 ，速度范围是 。

动态自适应PSO优化三段式神经网络钢温模型的预测结果如图1所示。

预测性能指标分析如表1所示。

表1 动态自适应粒子群优化三段式神经网络的钢温预测性能指标分析表

误差分析	最大绝对误差	平均绝对误差	方差	标准差
误差值（℃）	6.7749	1.9170	5.7981	2.4079

动态自适应PSO优化三段式神经网络钢温模型的预测误差分析图如图2所示。

由仿真结果可以看出，用动态自适应粒子群算法代替原标准的粒子群算法来优化BP神经网络是成功的，粒子群在每一次的迭代中都会根据自身搜索和种群收敛的情况自适应的调整惯性权重和学习因子，不再需要为了确定这几项参数的值而进行大量的仿真试验，并且在种群陷入早熟收敛时能及时的退出循环，大大提高了搜索的效率和速度，而且平均绝对误差和标准差等性能指标也明显减小，最大绝对误差是6.7749℃，大部分的误差分布均在 6℃之内，预测的精度和准确性明显提高。

5.结束语

本文主要介绍了利用粒子群算法来优化三段式神经网络的钢温预测模型。首先介绍了粒子群算法的起源、基本思想、特点、应用、基本及标准粒子群算法的原理；然后介绍了粒子群算法和神经网络结合的方式，用标准粒子群优化BP神经网络的具体过程，并给出了标准粒子群优化三段式神经网络钢温预测模型的仿真结果；接着根据粒子群算法的自身缺陷，重点介绍了动态自适应粒子群算法优化神经网络的实现过程，并用此改进的方法代替原标准的粒子群算法来优化钢温模型，最后给出了仿真结果并加以分析，证明了应用改进的自适应粒子群算法优化第三章中基于神经网络的钢温模型的合理性与可行性。

参考文献

[1]王锡淮,李柠等.步进式加热炉建模和炉温优化设定策略[J].上海交通大学学报，2001，35(9):1306-1309.

[2]吴成东.钢坯加热时传热数学模型的研究[J].沈阳建筑工程学院学报，1994，10(4):16-20.

[3]梁军.大型板坯届热炉中钢坯温度分布的软测量研究及实现[J].1999，20(1):81-83.

[4]毕春长.蓄热式加热炉钢温预报与炉温优化设定研究[J].自动化学报，2004，30(3):476-480.

[5]Jean-Luc,Roth.Computer control of slab furnace based on physical models[J].Iron and Steel Engineer,1986,56(6):41-47.

[6]巢海,王伟,李小平.步进梁式加热炉钢温预报的数学模型[J].东北大学学报，1998，19(5):499-501.

[7]石伟,陈海耿,宁宝林.以炉温为基准的炉膛总括热吸收率[J].钢铁，1997，32(4):69-72.

[8]梁军.自适应技术在加热炉控制中的应用[J].工业炉，1997，19(1):59-64.

[9]梁军.自适应控制系统的鲁棒性研究及应用[D].杭州：浙江大学，1993.

[10]H.J.Wick.Estimation of ingot temperature in a soaking pit using an extended kalman filter[C].Preprints papers for IFAC 8th triennial World Congress,1981,6(4):94-99.

[11]肖冬,杨英华,毛志忠.基于PCR改进方法的加热炉钢温预报模型[J].信息与控制，2005，34(3):340-343.

9