深究教材习题 巧解折叠问题

深究教材习题 巧解折叠问题

应国光

浙江省绍兴市诸暨市次坞镇秀松初级中学 浙江省 诸暨市 311815

内容摘要:

教材是执行课程标准与体现课改精神的载体,也是众多教育专家和一线教师智慧的结晶.教材上每个章节的每一道例题都有一定的教学目标,不仅如此,例题中的每一个问题,其背后都蕴涵着特定的意图.同样,各道练习题也有不同层次的要求与目标.需要我们进行深入的解读.只有这样我们对于解题才能更得心应手.本文以教材中的一题课后练习为基础,对其进行深入探究,提炼结论,并运用到一类折叠问题中,使问题更加的简便,达到了巧解的目的.

关键词:

教材 折叠 结论 能力

正文：

折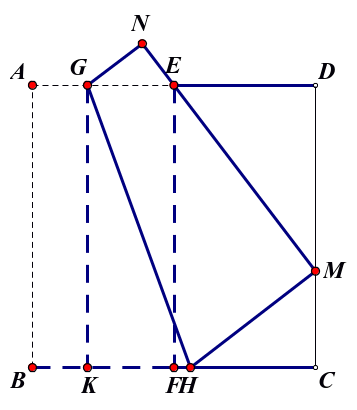 叠问题是近年来中考中出现频率比较高的热点、难点问题, 折叠问题题型多样,变化灵活,这对于识别和理解几何图形的能力、空间思维能力和综合解决问题的能力都提出了比以往更高的要求.折叠问题从图形看起来比较复杂,学生有点望而生畏不知从何下手。因此在教学中,教师应教会学生找其中的规律性。在正方形、矩形的折叠问题中,直角三角形,K形图是经常出现的,我们可以抓住重合的图形是全等的关系,三角形的相似关系找出隐含条件,牵线搭桥,找到解题的中间环节,起到画龙点睛的作用,使问题化难为易.

一、挖掘习题,碰撞思维

已知,如图1,将边长为6的正方形ABCD对折,折痕为EF,展开后再将点B折到边CD上的M处,使边AB经过点E,折痕为GH,点A的对应点为N.

(1)若CM=x,则CH= (用含有x的代数式表示);

(2)求折痕GH的长度

图1

遇到这类问题如何入手解答呢?根据以往解题经验,学生们认为,要学会联系上下文.是的,通常把关题的命制时,第(1)问的给出往往不是孤立的,它可能为后面问题的解答提供必要的条件或者解决问题的思路.当然,这与我们教师平时的训练分不开的,我们在平时教学过程中要学会适时留白,时常锻炼学生的思想方法,不要采取满堂灌的教学方法,让学生自主探究,独立去思考,解题时遇到这种关节就一定能够打通,解决这类问题就有可能会得心应手.经过他们研究可以发现,此问题(2)中解决问题的关键就是如何求出问题(1)中的x的值.那么,如何求x的值呢?

学生经合作探究得知,该图形里还包含一组相似三角形:△MCH∽△EDM,这组相似三角形的出现,成了另一种解题的关键.如果证明出这两个三角形相似了,就可以借助于相似三角形对应边成比例得出HC:DM=CM:DE,然后把CM=x,DM=6-x,DE=3,代入得CH:(6-x)=x:3,运用比例性质可得出 .由于CH表示同一条线段,因而可以建立等量关系式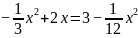 ,可求出 , 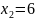(不合题意舍去),从而可得CM=2.

学生解答:由于求出线段CM=2,可知MD=4,由于DE=3,在Rt△MDE中,根据勾股定理可得ME=5 ,接着可求出EN=1.若设AG=m,则GN=m,GE=3-m,在Rt△GNE中,根据勾股定理 ,即 ,解得m=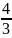 ,于是BK=AG= 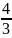,由于HC= 因而KH=6-BK-HC=6-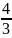 - =2.于是在Rt△GKH中,GK=6,KH=2,根据勾股定理, .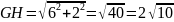

此题已经解出来了,但是仔细观察思考发现,上面的解法是按照常规思路解答的,过于繁琐,对于此问题的解决是否还有更好的途径呢?

二 、深究教材,提炼结论

教材中关于正方形的问题涉及的较多,能否从教材中探讨出来其它更为简捷的解法呢?经过探究教材发现,教材中的这道题对于解决此题第二问非常有利.

(浙教版八下第127页,作业题第4题)

如图在正方形ABCD中,E、F分别是BC、CD上的点,AE⊥EF,

求证：AE=BF.

这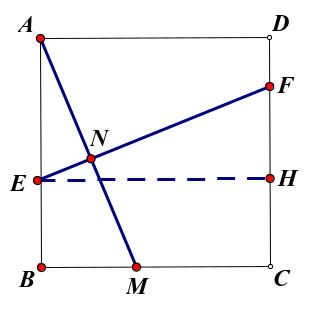 道题很容易就能证明△ABE≌△BCF,由此得到结论AE=BF.对于这一练习题,我们也可以进行初步的延伸.

如图2,在正方形ABCD中,E、F、M分别在ABCD、BC上,且EF⊥AM,垂足为N,那么EF与AM相等么?

图2

过点E作EH⊥DC,垂足为H,则∠EHF=∠B=90°.因为AB∥DC,所以∠EFH=∠AEF,因为EF⊥AM,所以∠BAM+∠AEN=90°,又因为∠BAM+∠AMB=90°,所以∠EFH=∠AMB,又因为AB=EH,所以△ABM≌△EHF,所以AM=EF.于是得出

结论1:正方形一组对边两点连线如果与另一组对边上两点连线互相垂直,那么这两条线段相等

如 果运用这一结论在正方形的翻折问题中,涉及到求折痕长度问题时,是不是可以使解题速度更快一些呢?

下面我们回过头来看一看问题中的第(2)问

(结论1的运用)如图3,连结BM,因为点B与点M关于折痕GH对称,所以BM⊥GH,因为正方形ABCD,所以有BMGH.在Rt△BCM中,BC=6,CM=2,根据勾股定理, ,

,根据结论1可得,GH=BM= .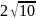

图3

这样解决问题思路很明确,问题变得更简洁,学生更容易理解和掌握.

以后遇到正方形中关于求折痕的长度问题时,可以根据上面的结论进行转化.需要注意的是,应当如何准确的找出另一条垂线呢?由上边问题可以知道,连结翻折后落在正方形边上的角的顶点与翻折前形成的对称点之间的线段,根据轴对称的性质,这两点的连线被对称轴平分.运用这个结论求正方形翻折问题中折痕的长度时,易求也易懂.

图4

三、延伸思维, 拓展变式

如图4,已知矩形ABCD中,点E在线段DC上,M、N分别在AD、BC上,且MN⊥AE,则MN: AE= AB: AD

过点M作MH⊥BC,易证明△MNH∽△AED,于是可证MN:AE=ABAD矩形翻折问题中,如果运用这一结论,也可秒杀折痕的求值问题

结论2:如果矩形中一组对边上两点之间的线段与另外一组对边上两点之间的线段互相垂直那么这两条线段的比等于不含该线段端点的矩形两条邻边的比值.矩形问题中十字交叉线的找法与正方形类似,正方形中的十字交叉线相等,矩形中的十字交叉线中的两条线段与矩形相邻两边成比例.

结论2的运用:

(1)直接运用:

例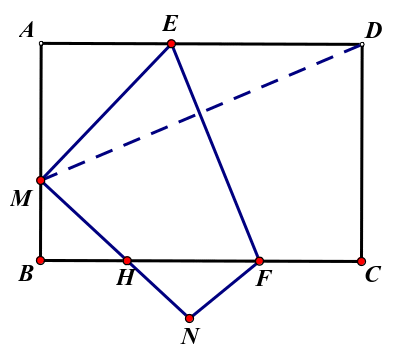 1矩形ABCD中,翻折边DC使点D落在AB边的M处,C落在N处,若AB=8,AD12,BM=3.求折痕EF长.

解析 如图5,本题如果运用结论2来解答,即可得到EF:MD=AB:AD=8:12=2:3,由勾股定理可求MD=13,因而EF=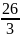

图5

四、吃透教材,提升能力

折叠问题中“折”是过程,“叠”是结果,其实质是轴对称变换,平面图形的折叠问题能够考查学生空问想象能力与动手操作能力及推理能力．这也是新课标对我们提出更高的要求．如果能发现折痕(对称轴)平移时对称点在一条定直线上运动的特征,在解决这类问题时,可以达到降低难度的目的．所以教师在课堂教学过程中要多挖掘一些行之有效的例题和习题,进行变式练习,发现问题的本质、规律,打开学生的思路,使学生的解题思路更为清晰,思维的应变能力得到充分的锻炼和培养．

在素质教育的今天,考试更重视考查学生的素质,教师必须多钻研新课程标 准,多研究教材,吃透教材,灵活应用教材．《初中数学课程标准》中指出：“数学教学活动应激发学生兴趣,调动学生积极性,引发学生的数学思考,鼓励学生的创造性思维；要注重培养学生良好的数学学习习惯 ,使学生掌握恰当的数学学习方法．教师教学应该学生的认知发展水平和已有的经验为基础,面向全体学生,注重启发式和因材施教．教师要发挥主导作用,处理好讲授与学生自主学习的关系,引发学生独立思考、主动探索、合作交流,使学生理解和掌握基本的数学知识与技能、数学思想和方法,获得基本的数学活动经验.

参考文献：

1.文志光. 浅谈中考中的折叠问题.素质教育论坛 2009 年 8 月(总第 112 期 )

2. 黄建阳.几种常见折叠问题.教学教育研究.2011年第33期

3. 金建伟 冯婷婷. 折叠问题中折痕平移的探索. 中学数学研究2017 年第 3 期 (下)

2