福建省漳州市漳州立人学校 363000
摘要:切线放缩法是解决导数不等式问题的一种常见方法,多次出现在高考试题中。本文主要通过利用两个常见切线放缩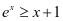 (1),
(1),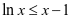 (2)来解决2020年新高考(山东卷)第21题第(2)问。
(2)来解决2020年新高考(山东卷)第21题第(2)问。
关键词:切线放缩;导数不等式
切线放缩是解决导数不等式问题的一种常见方法,在历年高考试题中曾多次出现。题目中若包含有对数、指数或者指对数混合的不等式,切线放缩的目的是将指数或者对数转变成一个常见函数或者一次,二次函数,从使导数不等式成立或者求含参数范围中把复杂问题简单化。
1.两个常见不等式证明
首先证明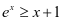 (1)
(1)
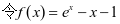 ,
,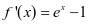 ,可得
,可得 ,
,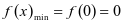 ,所以
,所以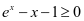 ,即
,即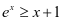 ,
, 。
。
用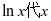 即可得
即可得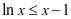 (2),当
(2),当 。
。
2.试题展示:
21.已知函数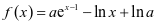 .
.
(1)当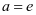 时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求a的取值范围.
3.考查目标
本题考查导数几何意义、利用导数研究不等式恒成立问题,考查学生的逻辑推理能力、综合分析求解能力,分类讨论思想和等价转化思想。
4.解法探究
本题的表达方式简洁明了,设问方式干净利落。第(1)问略,第(2)问主要考察导数在研究函数性质与不等式证明的应用即不等式恒成立求参数取值范围问题,解题方法较多,以下从多个角度用切线放缩来对第(2)问进行分析和求解。
第(2)问解法一:
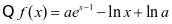 ,
,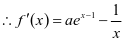 ,且
,且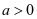 .
.
设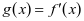 ,则
,则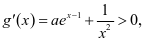 ∴g(x)在
∴g(x)在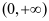 上单调递增,即
上单调递增,即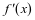 在
在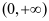 上单调递增,
上单调递增,
当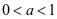 时,
时, 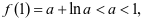 ∴
∴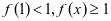 不是恒成立,不合题意。
不是恒成立,不合题意。
当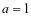 时,
时,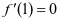 ,∴
,∴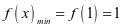 ,∴
,∴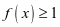 成立.
成立.
当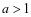 时,由(1)(2)式可得
时,由(1)(2)式可得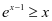 ,
,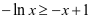 ,所以
,所以
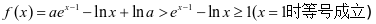
综上所述,实数a的取值范围是[1,+∞) 。
解法二:
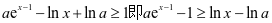 ,由(1)式得
,由(1)式得 ,只需证
,只需证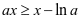 即证:
即证: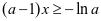
当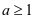 时,
时,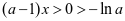 恒成立;当
恒成立;当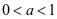 时
时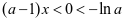 不合题意;
不合题意;
综上所述,实数a的取值范围是[1,+∞) 。
解法三:
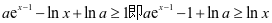 ,由(2)式得只需证
,由(2)式得只需证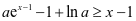
即证: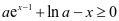 ,令
,令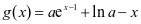 ,
,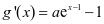 ,
,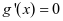 ,得
,得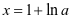 ,所以
,所以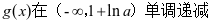 ,
,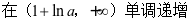 ,所以
,所以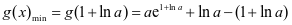 =
=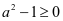 ,所以
,所以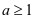 ;
;
又因为当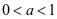 时,
时, 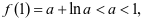 ∴
∴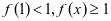 不是恒成立,不合题意。
不是恒成立,不合题意。
综上所述,实数a的取值范围是[1,+∞) 。
解法四: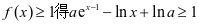 ,又
,又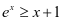 ,
,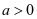 所以要证
所以要证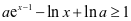 ,只需证
,只需证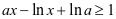 ,令
,令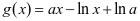 ,
,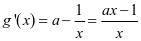 ,易得
,易得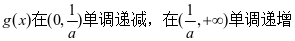 ,
,
所以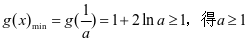 ,
,
又因为当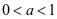 时,
时, 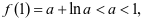 ∴
∴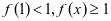 不是恒成立,不合题意。
不是恒成立,不合题意。
综上所述,实数a的取值范围是[1,+∞)。
解法五: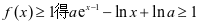 ,记
,记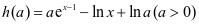 ,
,
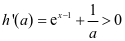 ,所以
,所以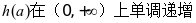 ,又因为
,又因为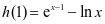 ,
,
由(1)(2)式可得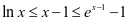 ,所以
,所以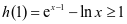 ,
, 。所以当
。所以当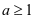 时
时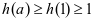 ,即
,即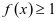 ,
,
又因为当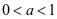 时,
时, 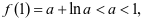 ∴
∴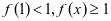 不是恒成立,不合题意。
不是恒成立,不合题意。
综上所述,实数a的取值范围是[1,+∞)。
总结感悟:函数、方程、不等式是高中数学的核心内容之一,是各类考试中重点考察的内容,本题作为一个含参不等式恒成立问题出现,题目矮小精悍,有效考察了学生处理问题的能力,凸显数学核心素养,用好两个重要的“切线不等式”,能达到化繁为简、以简驭繁的效果。
本论文系2019年度漳州市基础教育教学研究“数学科高考题型研究”课题(ZPKTZ19002★)的阶段性成果。
1