在“错误”中，让学习深度发生

在“错误”中，让学习深度发生

黄霞

福建省福州市闽清县实验小学

教育家苏霍姆林斯基曾经说过:“上课并不像把预先量好、裁好的衣服摆到布上去,问题的全部在于我们的工作对象不是布,而是有血有肉的,有着敏感而娇弱心灵和精神的儿童”。在平时的课堂教学过程中,学生肯定会出现这样或那样的错误,暴露出学生在学习过程中思维的不足。但是为了完成所谓的教学任务,尤其是在一些公开性的教学展示中,某些教师害怕学生答错,害怕学生出现一些不是在自己预设范围内的问题,当学生出现错误问题时,教师往往是令其坐下再想一想,而不让其陈述其中的理由。这样的课堂看似很顺利,实质是扼杀了学生的个性思维,新型教师应允许学生在课堂上犯错误。下面,是我在教学中对待学生出现的“错误”的一些做法。

一、在找“错误"中,培养学生观察能力

经常有学生在单元测试后高兴地跑来向我汇报:老师,这次我一定会得到好成绩的,所有的题目我都会做。但是,事与愿违,往往成绩和他们的预测相差甚远。学生在不知不觉中出现错误,而他们却浑然不知。教师应该有意识地让学生找“错误",促进学生观察能力的发展。

1.找同学的“错误”

在平时的教学过程中,学生经常出现一些好笑而又令人费解的错误,我时常让同学互相来找“错误”,每找一处"错误”,这个小组就能得到1分的奖励。这样学生乐于找“错误”,积极去观察,发现诸多学习中存在的问题。一道简单的题目,有时出现的错误类型是老师难以想象的。

如:水是由氢和氧按1:8质量比化合而成的,如果要化合7.2千克的水,需要多少千克的氧?

错例1: 7.2÷1+8=0.8(千克) 0.8x8=6.4(千克)

错例2: 7.2÷(1+8)=0.8(千克)

错例3: 7.2÷8=0.9 (千克)

错例4: 7.2÷ (1+8)=0.8(千克) 0.8x8=6.4(千克) 0.8+6.4=7.2(千克)

…

2.找老师的“错误”

人无完人,老师在课堂上也是难免出错的,我们要正自己的"错误”,让学生找老师的“错误”。老师在学生的心目中是完美无缺的,能发现老师的“错误”,对学生来说可能也是一种对自己的肯定,也是一种成功的体验。我鼓励学生找我的“错误”每找一处,这个小组将得到10分的奖励。一次公开课《平行四边形的面积计算》教学中,我在推导出公式后这样板书:平行四边形=底x高,并让学生齐读了一遍。这时一个学生站了起来老师：“你错了,平行四边形可以求周长,也可以求面积,甚至可以求角度,底x高只是求它的面积,所以应该加‘的面积’这3个字才比较完整”。 (全体学生都惊呆了)我是这样评价这位学生:观察仔细、善于发现、大胆指错、加10分。(全体学生鼓掌)

二、在议“错误”中,培养学生思维能力

在教学中学生所暴露出来的错误,往往是很具有典型性和普遍性的,当学生出现错误时,老师要保持沉默,让学生说说:你是怎么想的?为什么这样想?只有理解学生的错的理由,老师才能有针对性地讲评,千万不能轻易地给学生一个“错"的评价,而要找出学生错误中正确的地方,让美丽的错误生成出精彩的课堂。例如,在教学“某商店出售一种什锦糖,是由3千克的水果糖,2千克的奶糖和5千克的酥糖混合而成的，已知每千克水果糖10元，每千克奶糖是14元，每千克酥糖是12元，问每千克什锦糖应售价多少元？”此题一出，很快就有学生得出结论：

生1:根据“单价=总价÷数量”,应列式为(10+14+12)÷(3+2+5)=1.2(元)

生2:这个答案肯定是错的,因为最便宜的水果糖每千克都售价10元了,更何况什锦糖里还有更贵的奶糖和酥糖,它的单价肯定不会低于10元。

生3:每千克糖才1.2元,不符合生活实际。

生4:我有不同的意见。我的答案是12元,列式是这样的(10+14+12):3=12(元)

师问:你是怎么想的?

生4:什锦糖是由水果糖、奶糖和酥糖三种糖混合而成的所以它的单价应该和三种糖的单价有关,所以我就把三种糖的单价的平均数作为什锦糖的单价。

生5:我反对,这还没考虑到数量呢。这是一题求平均数的问题,应找出总数和份数。

师问:该怎样找出总数和份数呢?

生最终总结得出正确结论: (10x3+14x2+12x5)÷(2+3+5)=11.8（元）

通过学生的不断辩论,学生的思维发生碰撞,观点得到交流。错误也是一种教学资源,老师不要急于下结论,要引导学生从不同的角度去讨论错误,修正错误,给他们提供争论的时间,让学生获得良好的思维空间。

三、在比“错误”中,培养学生总结能力

一些抽象的数学题目是很容易让学生出错的,老师如果仅仅是用浅显的语言来讲评,学生还是不知其然,不知自己错在哪儿。如果把学生出现的错误进行比较辨析,找出它们的联系和区别,这样会得到事半功倍的教学效果。例如,在教学完分数应用题后,我出示了这样一题选择题:两根同样长的绳子,第一根用去了它的

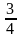,第二根用去了 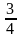米,哪根绳子剩下的比较长? A.第一根B.第二根C.同样长D.无法确定。结果答案五花八门,大家谁都认为自己的解法是对的。于是,我让学生用举例子的方法来证明自己的解法是对的。通过比较发现了这样的结论:选择A的同学,他们举例的绳长都小于1米,选择B的同学他们举例的绳长都大于1米,而选择C的同学,他们举例的绳长始终都等于1米。这时就有学生总结得出:绳子的具体长度是解题的关键,但是本题未给出明确的数据,所以答案也不能确定,只能选择D。

四、在改“错误”中,培养学生解决问题能力

学生在学习过程中所犯的犯错误,细加分析,或理解有偏差,或思维不够深刻,或看待问题的方式不同,老师如能对症下药针对错误,寻求正确解决问题的方法,许多问题都能有效地加以纠正,同时也能培养学生解决问题的能力。

总之,每个学生都是不同的个体,他们的学习基础、已有的认知起点都是不同的,在课堂上出错误是难免的、是允许的,这也是学生的权利。一位社会心理学家就曾说过:我们期望学生犯错误,因为从错误中吸取教训,便可争取明天的成功。我们老师要用资源的眼光看待错误,这是一个全新的视角。