抛物线的尺规作图方法-中国期刊网

首页 > 《教育学文摘》 > 2020年36期 > 抛物线的尺规作图方法

（整期优先）网络出版时间：2021-04-07

作者: 李恩斌1 李轩宇2

文化科学 >教育学

打印

同系列资源

/ 1

抛物线的尺规作图方法

李恩斌 1 李轩宇 2

1 四川省巴中市第二中学 636600 2 四川省巴中市奇章中学 636025

摘要：尺规作图是数学理性思维的体现，也是数学与艺术的结合，而抛物线是初中和高中数学中非常重要的内容，学习时往往需要数形结合，鉴于此本文给出五种抛物线的尺规作图方法，希望对各位读者理解尺规作图和抛物线有所帮助。

关键词：尺规作图、抛物线、数学思想

菱形法

图1

作法：1、建立如图1所示直角坐标系，O为坐标原点，直线L⊥x轴交于点M，F为x轴正半轴上一点，使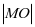 = 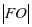。2、在x轴负半轴上任取一点A，以A为圆心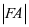，为半径作弧，交直线L于B，C两点。3、分别以B、C和F为圆心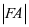，为半径作弧，分别交于点D、E，则D、E在抛物线上。4、同理可作出D₁，E₁，D₂，E₂……均在抛物线上，用光滑的曲线连接这些点，即得所求抛物线。

中垂线法

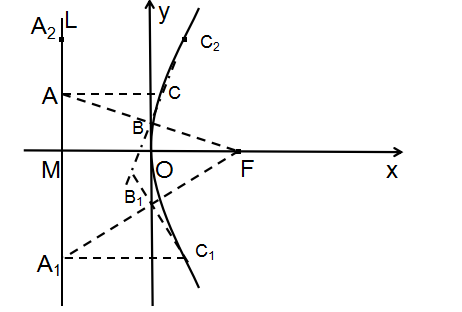图2

作法：1、建立如图2所示直角坐标系，O为坐标原点，直线L⊥x轴交于点M，F为x轴正半轴上一点，使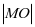 = 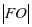。2、在直线L上任取一点A，连接FA交y轴于B点。3、过B点作FA的垂线，再过A点作x轴的平行线与该垂线交于点C，则C在抛物线上。4、同理可得C₁，C₂……均在抛物线上，用光滑的曲线连接这些点，即得所求抛物线。

垂线作弧法

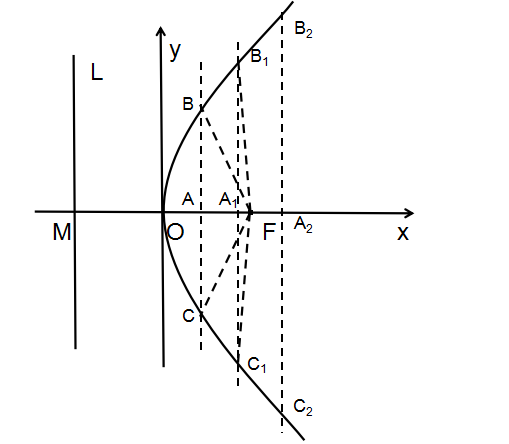图3

作法：1、建立如图3所示直角坐标系，O为坐标原点，直线L⊥x轴交于点M，F为x轴正半轴上一点，使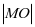 = 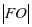。2、在x轴正半轴上任取一点A，过A作x轴的垂线。3、以F为圆心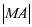，为半径作弧，交该垂线于B、C两点，则B、C在抛物线上。4、同理可得B₁，C₁，B₂，C₂……均在抛物线上，用光滑的曲线连接这些点，即得所求抛物线。

等角法

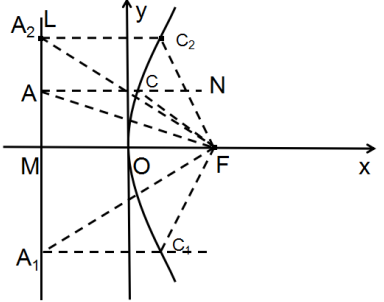图4

作法：1、建立如图4所示直角坐标系，O为坐标原点，直线L⊥x轴交于点M，F为x轴正半轴上一点，使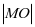 = 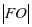。2、过点F作直线FA交L于点A，过点A作x轴的平行线AN。3、在直线AN上找一点C，作∠AFC=∠CAF，则点C在抛物线上。4、同理可得C₁，C₂……均在抛物线上，用光滑的曲线连接这些点，即得所求抛物线。

相交法

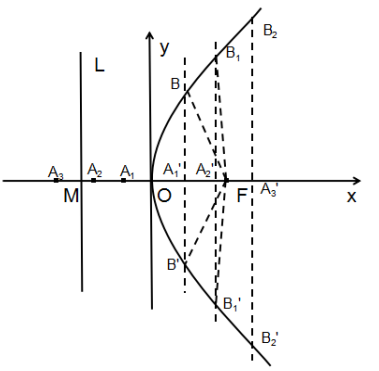图5

作法：1、建立如图5所示直角坐标系，O为坐标原点，直线L⊥x轴交于点M，F为x轴正半轴上一点，使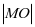 = 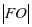。2、在x轴负半轴上任取一点A₁，以F为圆心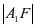，为半径画圆弧。3、在x正半轴上取点A₁’，使 = 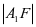,过点A₁’作x轴的垂线，与圆弧交于点B、B’，则B、B’在抛物线上。4、同理可得B₁、B₁’、B₂、B₂’……均在抛物线上，用光滑的曲线连接这些点，即得所求抛物线。