DEH阀门特性在线分析与诊断技术

DEH阀门特性在线分析与诊断技术

高鹏义

内蒙古能源发电投资集团有限公司电力工程技术研究院 010020

摘要：本文提出的DEH阀门特性在线分析与诊断方法，使用自学习回归神经网络算法模型，以机组运行过程的历史数据为模型训练数据，以期望的特征变量为响应输出和预测输出，在机组正常运行中求出DEH阀门开度-流量特性曲线，从中分析诊断出阀门存在的问题和严重程度，指导运行人员有针对性将问题解决在萌芽状态，杜绝小问题酿成大故障，为提高机组安全、稳定、高效、经济运行水平提供切实可行的技术手段。

1. 背景

汽轮机电液调节系统（DEH）的关键执行机构-电液伺服阀、油动机及阀芯在机组长期在线运行时始终处于开-关往复运动状态，由于反馈机构的机械漂移、控制信号电气漂移、阀芯的机械磨损、汽蚀和故障造成的损伤等原因，造成当下阀门实际流量特性曲线与当初设定值发生偏离，引起运行中阀门振荡，而这种振荡故障若不早消除会加速发展，严重时会造成功率难以控制、单顺阀切换困难、自动发电控制（AGC）和一次调频等调节性能下降、机组协调响应能力不足等现象。常规解决办法是在机组停机时重新校正DEH系统，仍不能解决时申请调度安排调阀流量测试试验，根据测试结果修改当初的设定曲线，还不能解决时将阀门返厂处理。从整个常规解决过程看出，阀门特性出现问题时发现晚，总是在问题比较严重时才能发现；解决问题费时，影响正常生产，经济性差。如何快速发现问题并表达出问题的严重程度和解决办法而尽量不影响生产，是当下智能数字化技术的一个研究方向。

2. 自学习回归神经网络算法

自学习回归神经网络模型描述响应（输出）变量与一个或多个预测（输入）变量之间的关系。拟合模型后，就可以使用模型来预测或仿真响应，使用假设检验来评估模型，或者使用绘图来可视化诊断、残差和交互作用。具体原理已有大量文献介绍不再赘述，下面主要介绍基于该算法的2个典型应用案例。

1. 1. 故障阀门的在线分析与诊断

某C320/248-16.67/0.8/538/538型汽轮机DEH阀门配置如图：

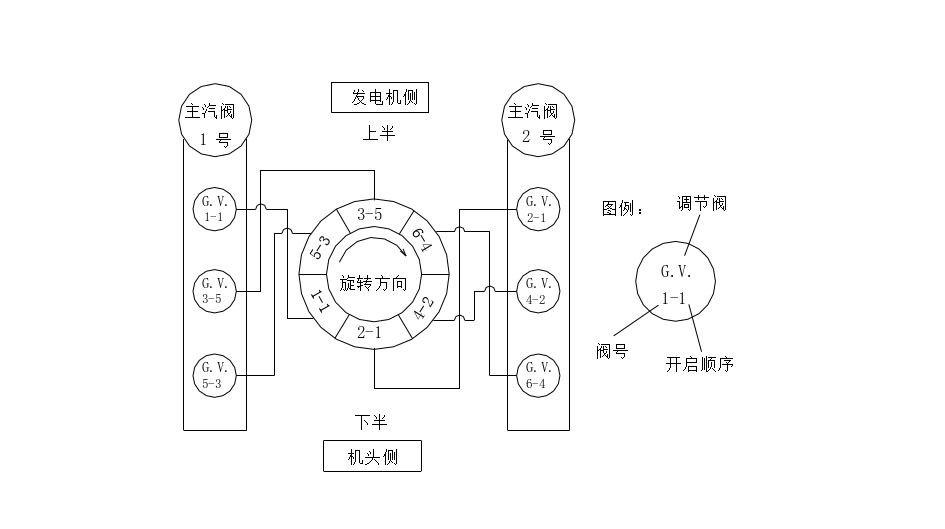
图1 DEH阀门配置

采集输入变量17个：电功率、主汽压力、主汽温度、调节级压力、调节级温度、一抽压力、一抽温度、高排压力、高排温度、背压、GV1指令、GV2指令、GV3指令、GV4指令、GV5指令、GV6指令、主汽流量。每个变量采集样本数8400个，采样间隔2秒一个，共计总样本数142800个。

响应输出变量1个：主蒸汽流量。

预测输入变量6个：GV1指令、GV2指令、GV3指令、GV4指令、GV5指令、GV6指令。

拟合自学习回归神经网络模型6个：trainedModel_GV1_0~trainedModel_GV6_0。

基于自学习回归神经网络模型DEH阀门在线分析与诊断结果如图2所示：

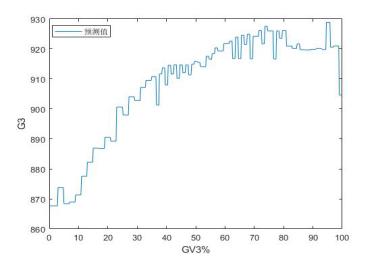
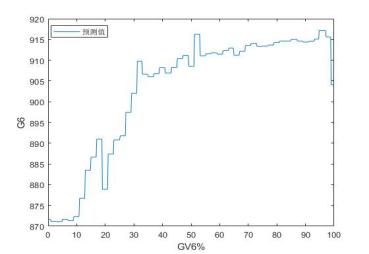
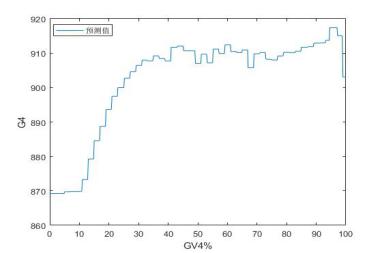
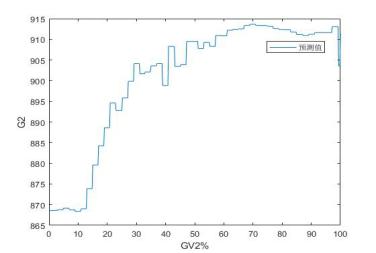
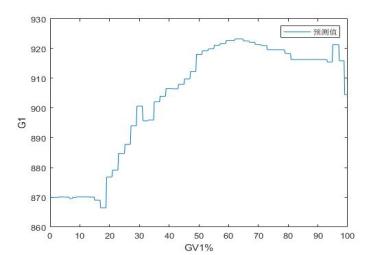
图2 GV1~GV6阀门特性分析诊断结果

由图2所示各阀特性曲线可知：

1）每个GV阀不同程度地存在不同位置的控制回差，沿阀门开度增长方向流量波动剧烈。说明要么电液伺服阀校正不好，灵敏度差，阀门指令与实际阀门位置线性度不好；要么在这些位置阀芯出现了问题。

2）个别GV阀预启行程大，最大GV1达到20%左右，其它也达10%。这在顺阀运行时尤其是阀门重叠过渡位置流量肯定难以控制。

该机组实际运行情况确实如此，机组长期单阀运行，且负荷控制很差，单顺阀切换过程负荷波动剧烈，故一直无法切换至顺阀。

1. 2. 正常阀门的在线分析与诊断

某CZK330/272-16.67/0.4/538/538汽轮机DEH阀门配置如图3所示：

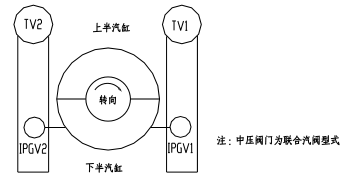
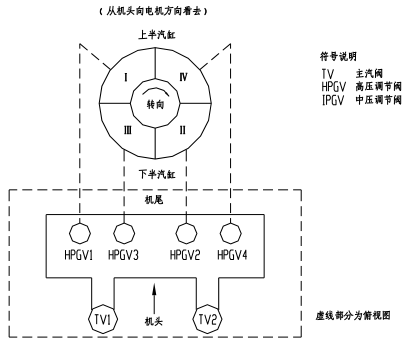
图3 DEH阀门配置

采集输入变量15个：电功率、主汽压力、主汽温度、调节级压力、调节级温度、一抽压力、一抽温度、高排压力、高排温度、背压、CV1指令、GV2指令、GV3指令、GV4指令、主汽流量。每个变量采集样本数1500个，采样间隔2秒一个，共计总样本数22500个。

响应输出变量1个：主蒸汽流量。

预测输入变量2个： GV3指令、GV4指令。

拟合自学习回归神经网络模型2个：

trainedModel_GV3_0 、trainedModel_GV4_0。

基于自学习回归神经网络模型DEH阀门在线分析与诊断结果如图4所示：

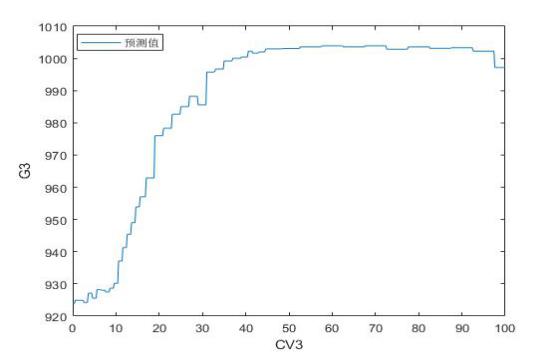
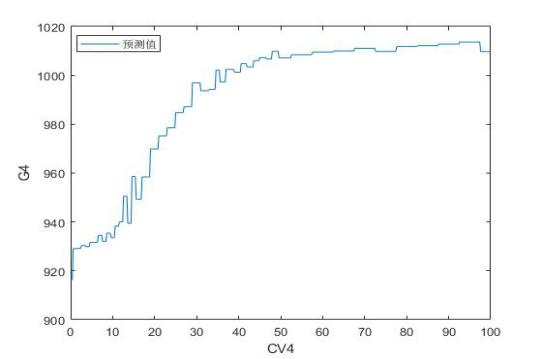
图4 GV3 GV4阀门特性分析诊断结果

由图4所示各阀特性曲线可知：

1）GV3阀有2点存在10t左右流量跳变，预启行程在10%左右流量渐变明显。阀门拐点位置清晰。其他位置线性度良好。

2）GV4阀存在2个5%左右行程区间线性度不佳，阀门拐点位置清晰。其余位置线性度良好。

该机组实际运行情况确实如此，机组单顺阀切换正常，负荷控制理想。采样数据来源于只对长期带负荷顺阀运行的GV3、GV4的特性试验。

1. 3. 对其他变量的分析诊断

在不得已对DEH阀门进行流量特性试验时，一个重要试验条件就是保证主汽参数稳定。究其原因，是因为试验过程中主汽参数的波动会造成流量信号的波动，一般各电厂的主汽流量都按调节级压力进行计算，即主汽流量等于调节压力的线性化。实际上汽轮机厂给出的主汽流量与调节级压力关系曲线也是线性化的。那么，实际上调节级压力与主汽流量的关系、主汽压力与主汽流量等的关系到底是怎么样的，自学习回归神经网络算法能对这些相关变量进行识别吗？答案是肯定的。下面列出辨识结果：

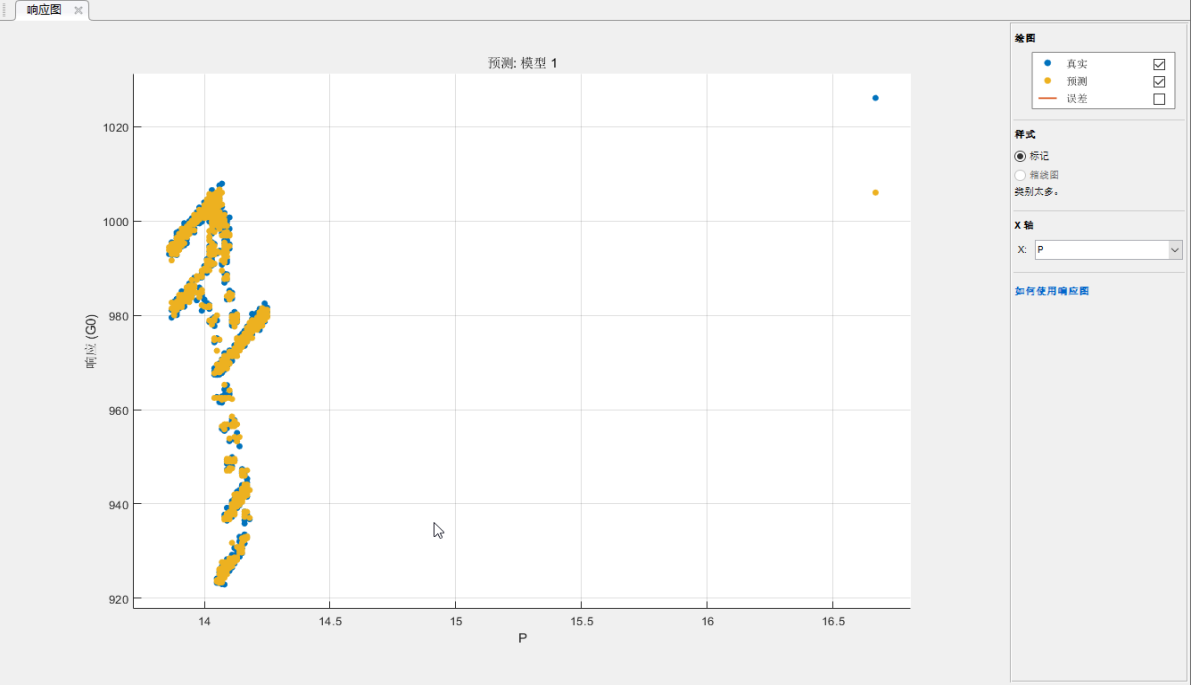
图5 试验过程中主汽压力对主汽流量的影响

从图5可以看出，在整个试验过程中主汽压力波动约0.2MPa，影响流量约14t，即如果主汽压力波动控制在0.2MPa时，整个试验过程按额定流量1026.1t算，精度约为1.4%。这也表明试验过程如果取调节级压力线性化的主汽流量信号，在主汽压力波动0.2MPa时其试验误差约为1.4%。为了消除或尽量减少这样的误差，有的试验公式往往采用改进了的弗流格尔公式(1)对主汽压力波动加以修正。

0. 额定工况

1. 调节级后

2. 一抽

d-调节级、高排或一抽

G-流量

P-压力

v-比容

那么修正后，效果如何呢？见下图：

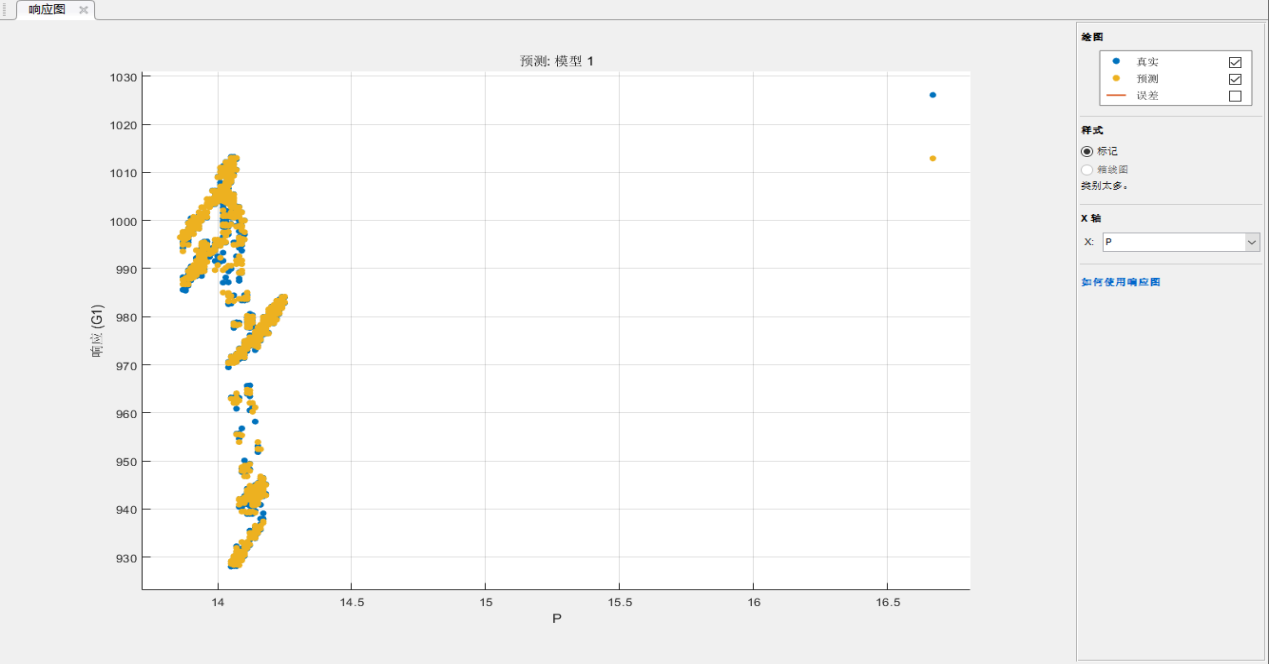
图6 d为调节级时计算的主汽流量

主汽压力最大变化0.2MPa，影响流量18t，误差1.75%。

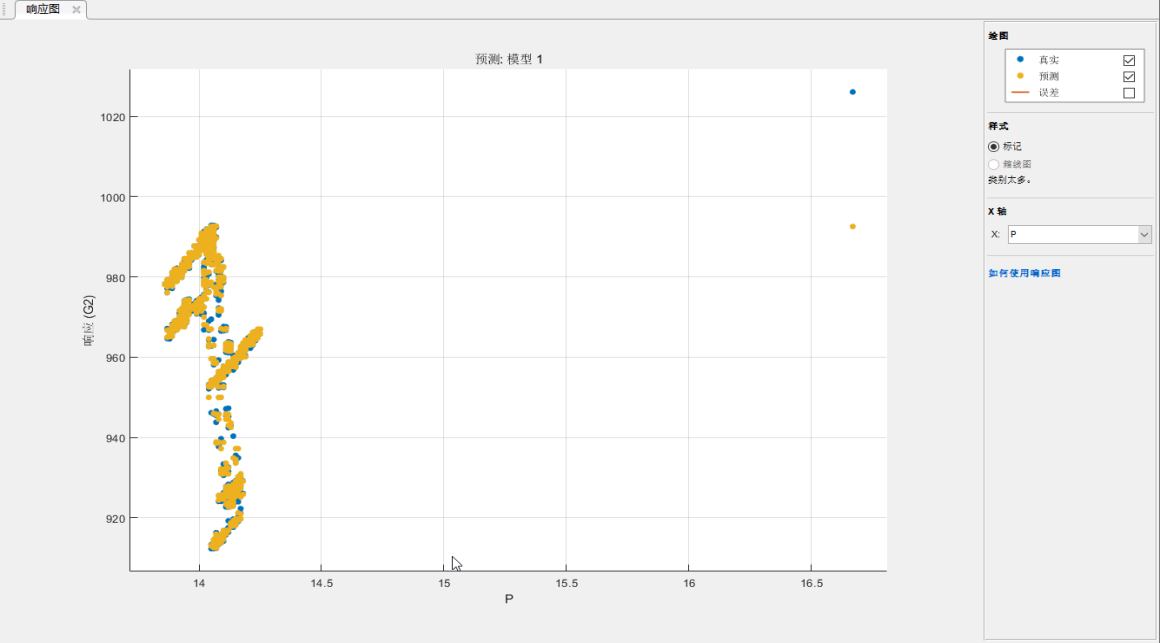
图7 d为一抽时计算的主汽流量

主汽压力最大变化0.2MPa，影响流量15.1t，误差1.47%。

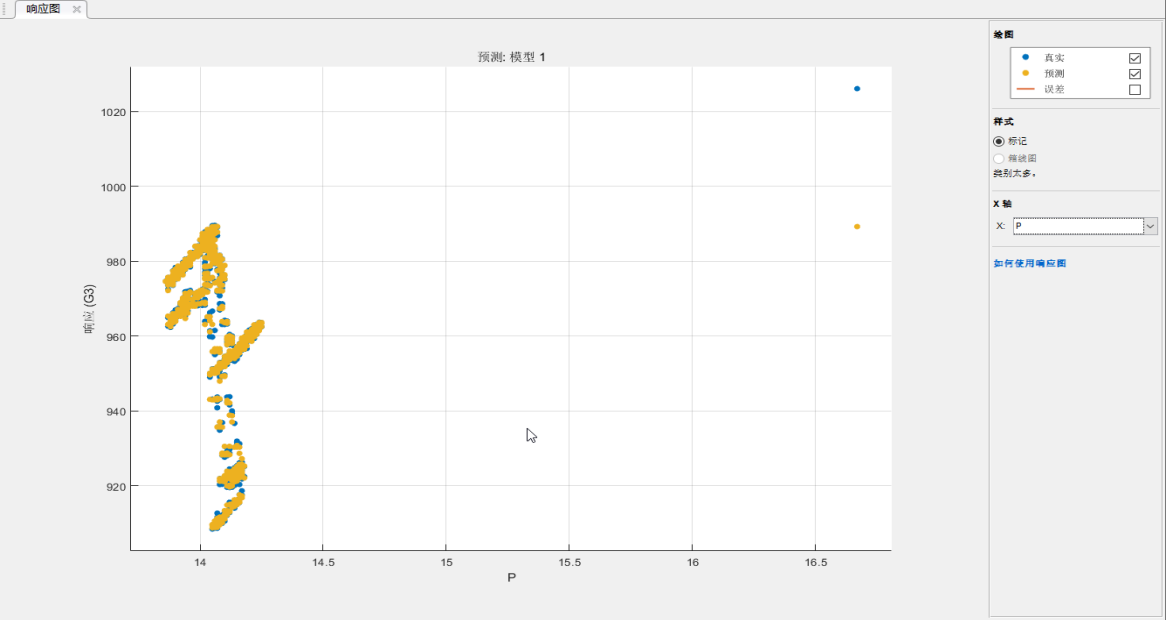
图7 d为高排时计算的主汽流量

主汽压力最大变化0.2MPa，影响流量15.67t，误差1.53%。

比较上述各计算公式，采用改进的计算公式计算值离散度较小，d取一抽计算精度与调节级压力线性化公式相当，所以建议选取一抽参数的改进计算公式。

那么，调节级压力与蒸汽流量的线性特性，自学习回归神经网络算法辨识结果如何呢？见下图：

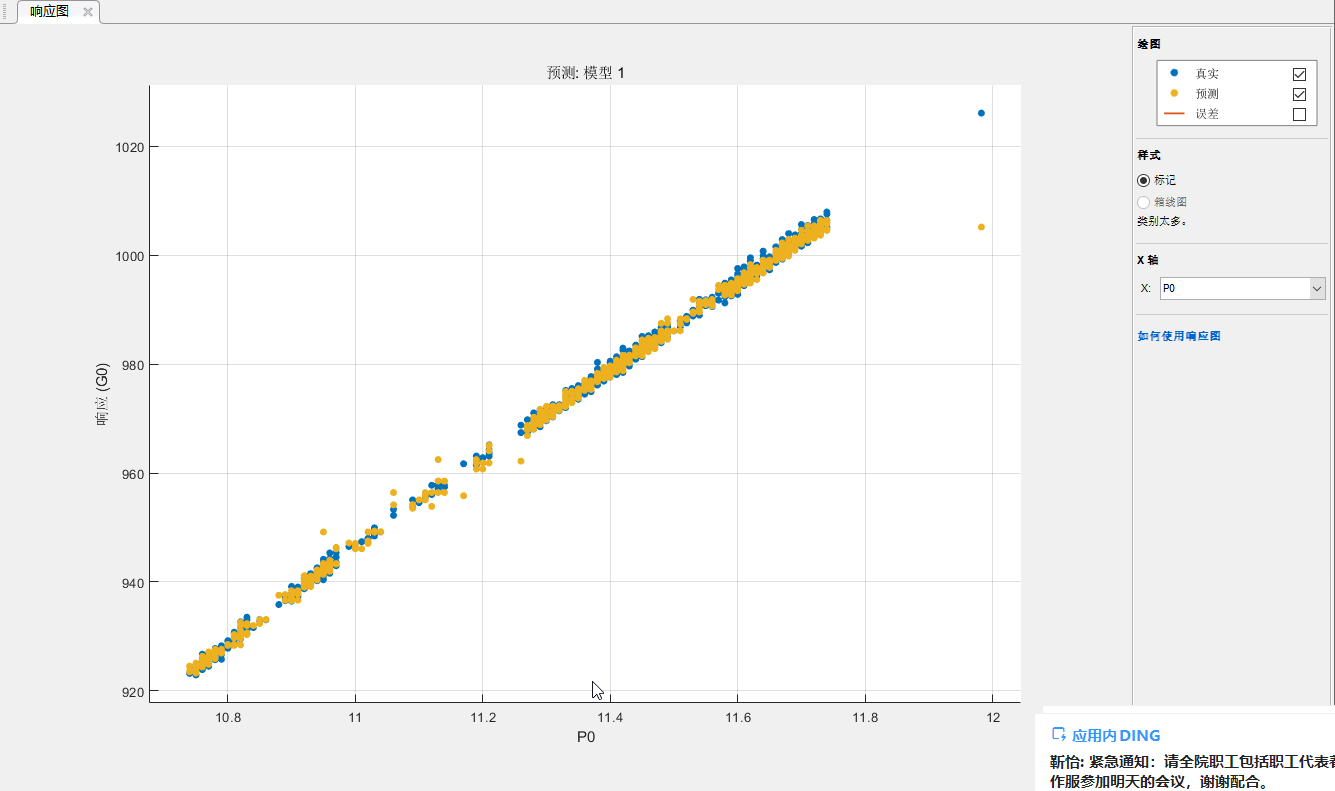
图8 调节级压力线性化计算蒸汽流量

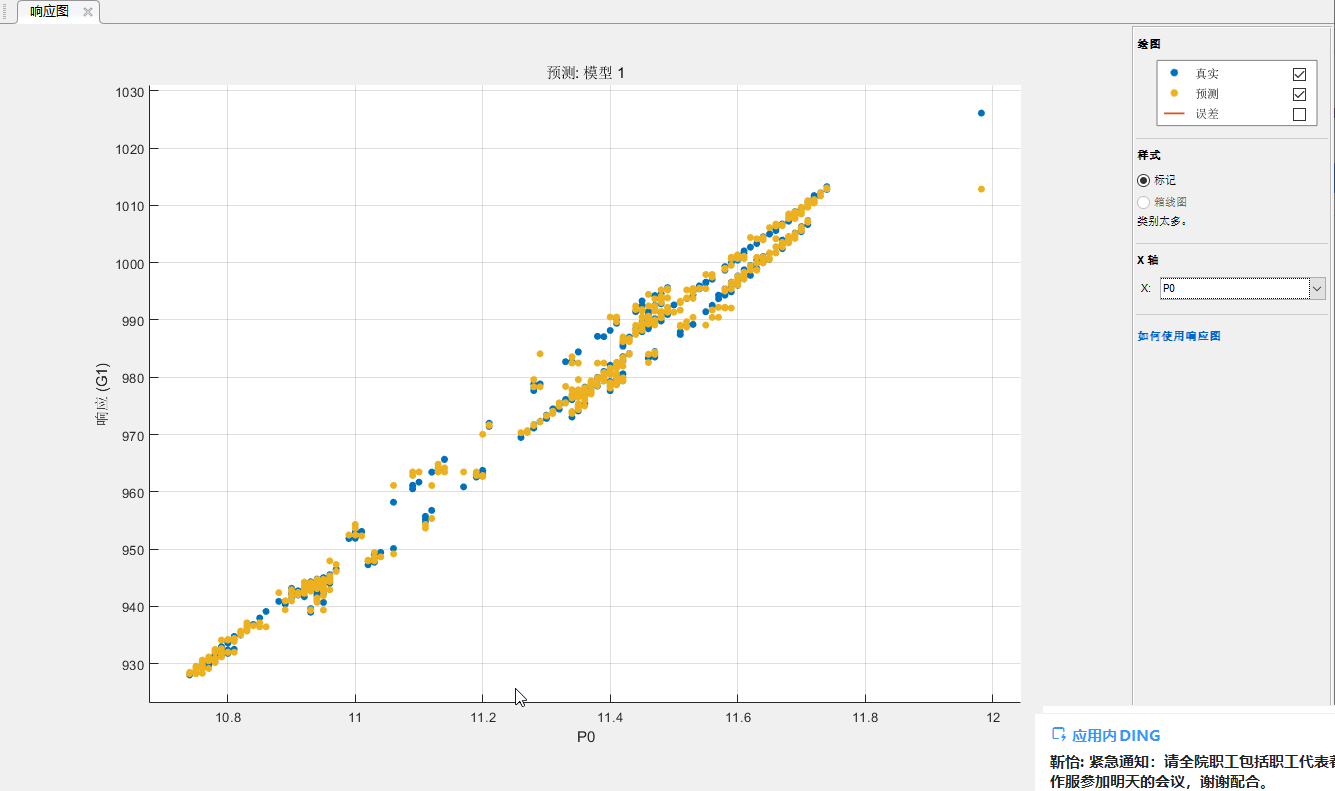
图9 d为调节级改进公式计算蒸汽流量

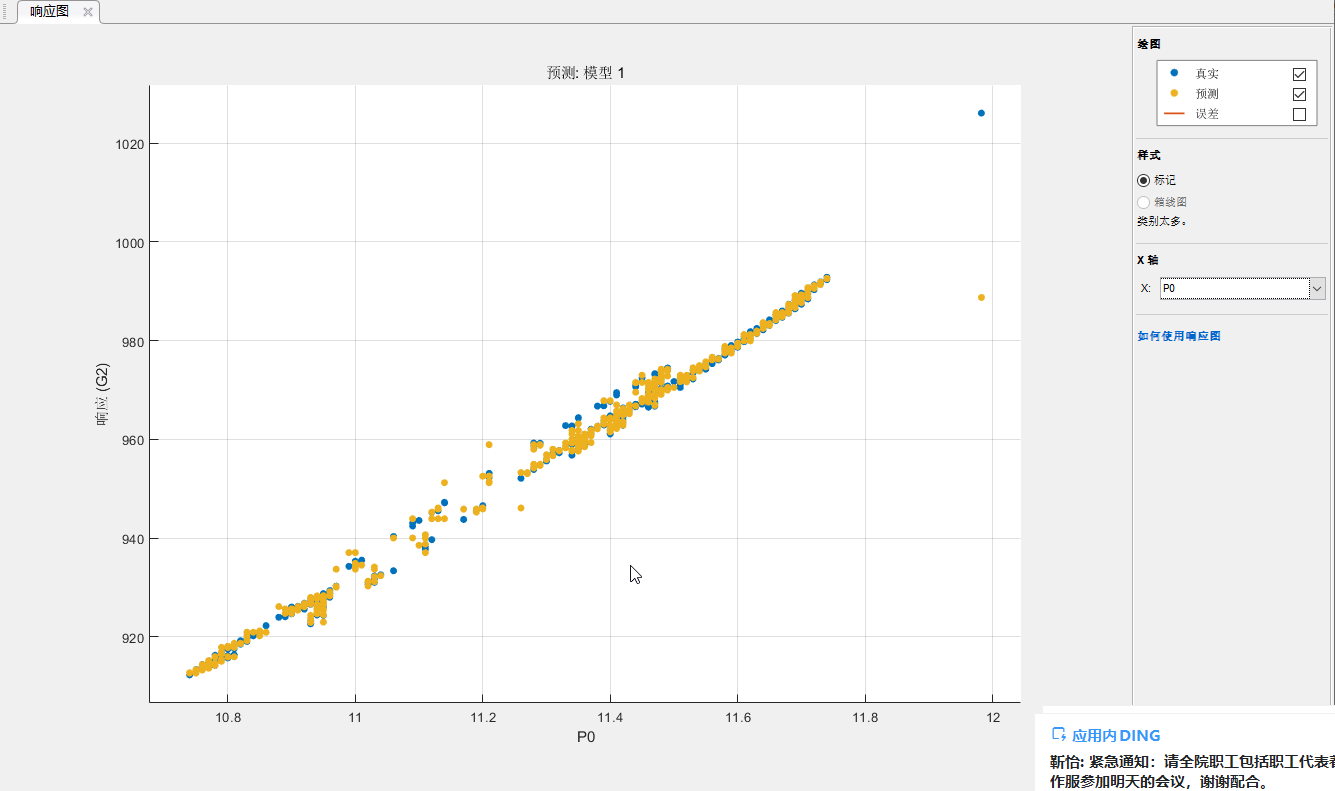
图10 d为一抽改进公式计算蒸汽流量

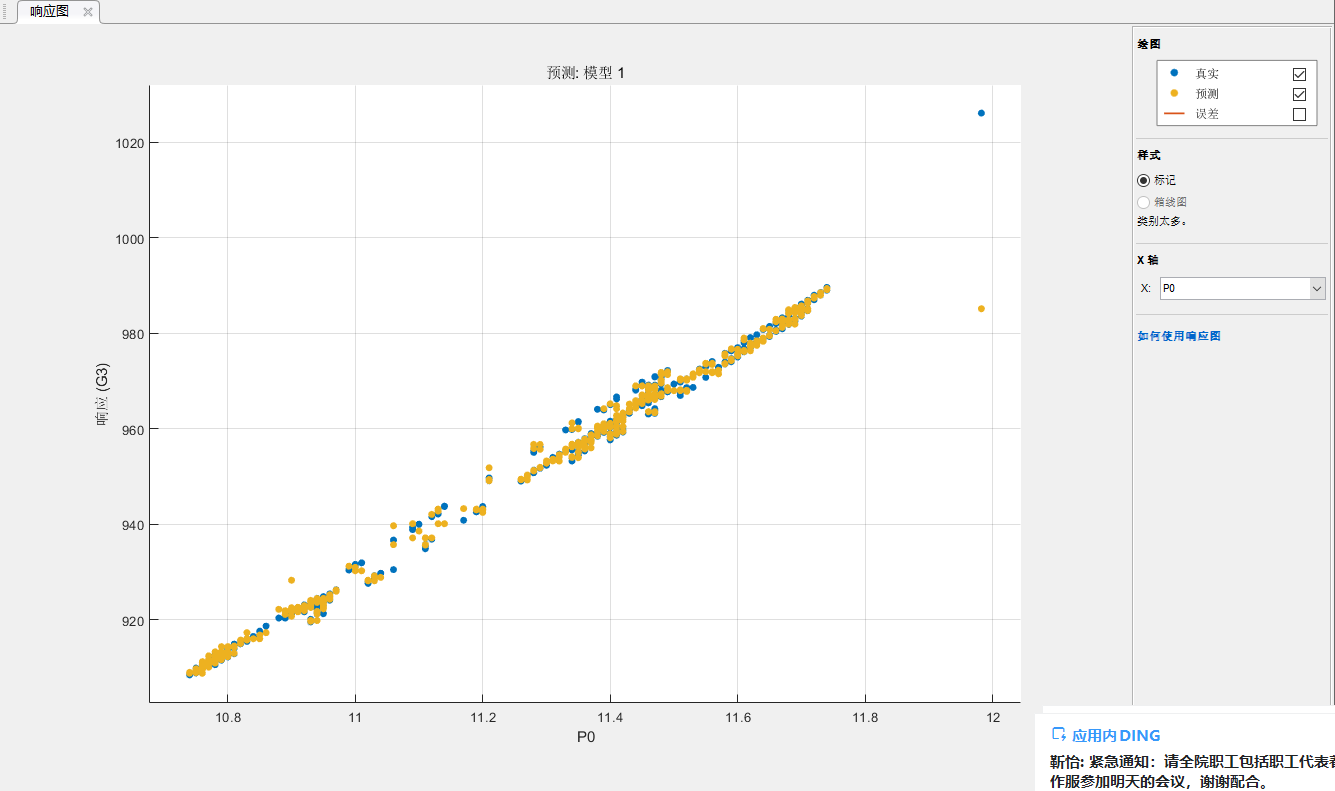
图11 d为高排改进公式计算蒸汽流量

由上图可知，图8纵坐标主汽流量本身是横坐标调节级压力的线性化结果，因此辨识结果是高度线性拟合的，而图9、图10、图11并不是调节压力的线性化结果，进行了不同参数的开方计算，实际辨识结果却都是线性的，图9计算结果离散度较大些，图10、图11接近，但较图9略差些。

3. 结束语

通过自学习回归神经网络算法对多变量系统中任意相关变量之间关系的大数据辨识和期望特征值提取，可以准确分析和诊断相关变量之间的性质和数量关系，对于多变量系统，尤其是变量间机理不清的系统，自学习回归神经网络算法的优势再明显不过，上述3个例子说明，此方法不仅用于相关变量间特性的分析与提取，还可用于故障诊断与预警，提取特性后可进一步进行优化等技术处理，对于智能数字化领域技术优势明显，值得推广。