抛物线中的“多题一解”

抛物线中的“多题一解”

李梦

沈阳市二十七中学

抛物线是圆锥曲线的一种，抛物线的形式为或 。这种“一个一次，一个二次”的形式决定了抛物线有自己独特的魅力，有它区别于其他圆锥曲线的地方，值得我们去深入探究。为此也经常受到命题者的青睐。

一、高考实例

例1.（2013年广东）已知抛物线 的顶点为原点,其焦点 到直线 : 的距离为 .设 为直线 上的点,过点 作抛物线 的两条切线 ,其中 为切点.

(Ⅰ) 求抛物线 的方程；

(Ⅱ) 当点 为直线 上的定点时,求直线 的方程；

(Ⅲ) 当点 在直线 上移动时,求 的最小值.

(Ⅰ)抛物线 的方程为 .

(Ⅱ) 抛物线 的方程为 ,即 ,求导得 设 , (其中 ),则切线 的斜率分别为 , ,

所以切线 的方程为 ,即 ,即

同理可得切线 的方程为

因为切线 均过点,所以,

所以 为方程 的两组解.

所以直线 的方程为.

以上解决问题(Ⅱ)的方法我们在解决椭圆和双曲线的切线问题中也都用到，可以把这类分题统称为切线问题的拓展———切点弦问题，而解决这种问题的方法我们称之为同一法，在上述方法中我们看到只要用到切点弦方程，我们就可以用这种方式来求切点弦方程。下面我们继续探究问题(Ⅲ)

(Ⅲ) 方法（1）：由抛物线定义可知 , ,

所以

联立方程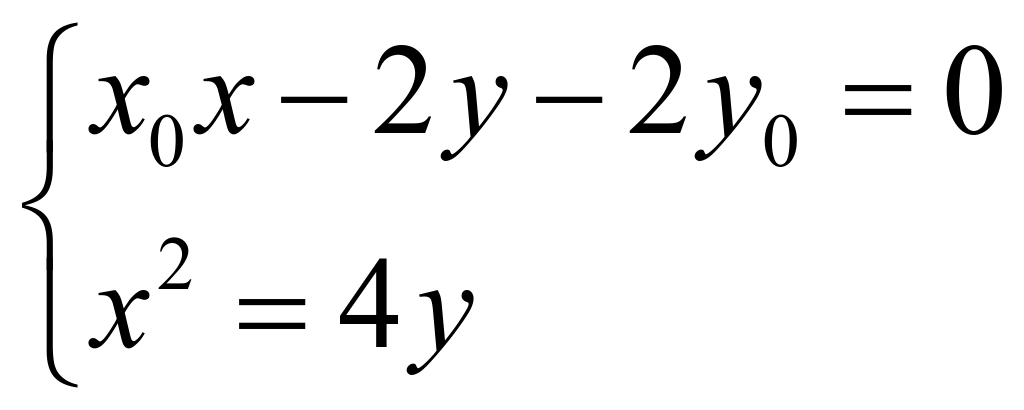 ,消去 整理得

由一元二次方程根与系数的关系可得 ,

所以

又点 在直线 上,所以 ,

所以 所以当 时, 取得最小值,且最小值为 .

因为前面的(Ⅱ)已经用两条切线的交点来表示切点弦方程，所以接下来的问题(Ⅲ)，我们会想到接着用这条切点弦的方程与抛物线方程联立，从而把最后的最值问题又转化成了我们以往对韦达定理的常规应用。但是如果把第(Ⅲ)问抽离出来，当我们只面对(Ⅲ)，而没有(Ⅱ)的铺垫，这样的做法未免舍近求远。下面我们用另一种方法来独立解决问题(Ⅲ)。

方法（2）：抛物线 的方程为 ,即 ,求导得 设 , (其中 ),则切线 的斜率分别为 , ,

所以切线 的方程为 ,即 即 ，可得同理可得切线 的方程为

因为切线 均过点 ，所以，

所以是方程即方程的两根

所以 ；,

接下来的做法同方法（1）

方法（2）之所以可以畅通无阻，恰恰是由于抛物线具备这种 “一个一次，一个二次”的形式，我们可以轻而易举的用二次来表示一次。在以上方法（2）的操作中也是用到了同一法的思想。

二、方法归纳

综合问题(Ⅱ) 和问题(Ⅲ)我们可以总结出抛物线切线问题的一般解决方式。

若为抛物线上一点，则抛物线在处的切线方程的两种形式为形式；

形式 对应解决两类问题如下：

若为抛物线外一点，过向抛物线引两条切线，切点分别为,求出所在直线方程

，即求切点弦方程用形式

对于其他问题我们都使用形式。其他问题主要包括只写出一条切线方程，或求两条切线两个切点之间的关系：求

， ； ， ；

这些问题在我们的平时练习及高考中层出不穷，具体如何应用，我们拭目以待。

三．具体应用

例2.已知曲线 ， 为抛物线外的点，过 向抛物线 引两条切线，切点分别为 ,（1）若 为直线 上动点，求证：直线 过定点

（2）若直线 过定点 ，求证： 为直线 上动点.

此题是极点极线问题的一种特殊情形。证明的关键就在于设 ，则切点弦的方程可以用表示为：从而能证明（1）反之能证明（2）用到的是上面的形式

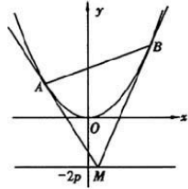
例3.（2008年山东） 如图，设抛物线方程为 ， 为直线 上任意一点，过 引抛物线的切线，切点分别为 ，

（1）求证： 三点的横坐标成等差数列；（2）已知 时， ，求此时抛物线的方程

可设，，此题证明（1）即证所以用上面的形式，对于问题（2）的处理，只需用上面的形式将写成：，与抛物线方程联立，借助弦长公式即可求出

例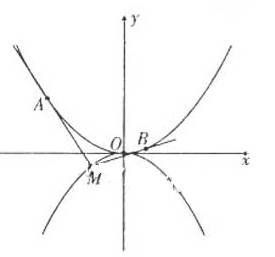 4.（2013辽宁） 如图，抛物线

（I）；

（II）

（I） ；（II）设 ， ， ，

因为 所以 + = ，

.只需用上面的形式 得出

=于是得到

例5.（2011课标）在平面直角坐标系 中，已知点 ， 点在直线 上， 点满足 ， ， 点的轨迹为曲线 .

（Ⅰ）求 的方程；

（Ⅱ） 为 上的动点， 为 在 点处的得切线，求原点 点到 距离的最小值

（Ⅰ） （Ⅱ）只需用上面的形式 设的方程为 ，接下来利用点到直线距离公式，看作关于 的函数即可解决问题.

四．感悟启示

以上几道习题其实是一类问题，都是在反复利用抛物线切线方程的两种形式。圆锥曲线问题是高考的一个区分点，因为这道题既考查了学生分析问题的能力，又考查了学生的计算能力。这个板块的题纷繁复杂，如果不能理清头绪，看到问题的本质，解决起来如同大海捞针。特别对于高三学生的复习，必须让学生一探究竟，才能在面对具体问题时，找对方向。无论这道题的外表如何包装与叙述，只要看到内核与本质，就能化繁为简，让繁难的运算变得轻松自如。从而让学生能够敢于面对圆锥曲线，不是逃避，而是层层剥离，理解精髓，用系统化的知识把看似散落的习题与分布的知识点串在一起。冲破束缚，迎战高考。