寻找特殊图形 洞悉隐藏玄机

寻找特殊图形 洞悉隐藏玄机

卢剑威

广东省佛山市顺德区勒流江义初级中学

对于许多初级中学的学生来说，学数学不算难，做数学才是难，做几何方面的数学题就更加难了。原因何在？就在于有些几何题目根本不知道该怎样下手，思维的源泉犹豫遇到了一堵坚固的门，流淌不过来；一旦发现玄机所在，思维的源泉就会奔流不息。如何指导学生发现题目的这个玄机并由此激发学生的兴趣呢?下面我就北师大版的《数学》九年级上下册的一些题目，谈一下洞悉题目中隐藏的玄机的一个方法：寻找特殊图形。

为什么要寻找特殊图形呢？其实道理很简单，特殊图形之所以特殊，就在于这些图形蕴含了大量特殊的性质，特别是关于线段与线段之间的数量、位置关系，利用这些性质与关系我们就可以很快的找到解决题目的通途。

那么，有哪些常见的特殊图形呢，如何利用它们呢？现举例如下：

1. 特殊四边形＋特殊角60º

这里的特殊四边形主要指：菱形，矩形，等腰梯形。这三种四边形与60º结合起来，就会出现等边三角形，简单概括如下：

菱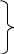 形

矩 形 ＋ 60º 等边△

等腰梯形

例1、（矩形＋60º）矩形ABCD的两条对角线相交于点O，已知∠AOD =120º，AB=2.5㎝，求矩形对角线的长。（上册课本87页例题）

分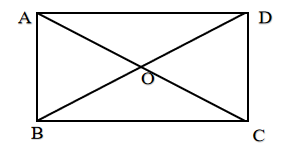 析：如右图所示， ∠AOD =120º

∠AOB =60º 等边△AOB

AO=AB=2.5㎝

AC=2AO=5㎝

小结：等边三角形有时候也会以30º或120º的隐蔽形式出现，所以，凡是遇到特殊角度就要多个心眼。

二、特殊的直角三角形

直角三角形本身就是特殊图形，因为直角三角形的直角为我们求角的度数提供了一些数据，直角三角形中的勾股定理是我们求解边的长度的有力工具。特殊的直角三角形，除了30º、45º或60º的直角三角形外，还有一些由常用勾股数，如3、4、5和5、12、13等组成的直角三角形。

例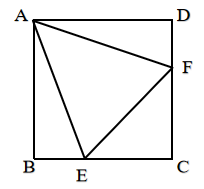 2、（等腰Rt△）如图，在正方形ABCD中，等边三角形AEF的顶点E、F分别在BC和CD上。若△AEF的边长为 ，求正方形的边长。

分析：从图上我们可以看到三个特殊的图形：

正方形、等边三角形、等腰直角三角形。

由等腰Rt△CEF的斜边EF= ，易得CE=1。

从而，设BE=x，AB=BC=1＋x,在Rt△ABE中， 由勾股定理得：（1＋x）²＋x² =²，解一元二次方程可得。

现在剩下的工作就是证明Rt△CEF是等腰的，即证明CE=CF或∠FEC=∠EFC。只要证明了△ABE≌△ADF（HL），问题迎刃而解。

小结：本题由三种特殊图形组合而成，并在题设中把“等腰直角三角形”这一条件隐藏起来。发现等腰Rt△CEF并不难，难就难在意识到EF是等腰Rt△CEF的斜边，并通过勾股定理和二次方程把三种图形的特性有机地串联起来。

三、特殊的中点与特殊的线段

中点的特殊性体现在它是很多特殊线段的重要组成部分，而特殊的线段往往又是题目的要害所在。与中点紧密结合的特殊线段主要有：线段的垂直平分线、三角形内的中线和中位线。

例3、（斜边上的中线＋底边上的中线）如图，在四边形ABCD中， ∠ABC=∠ADC=90º，M、N分别是AC、BD的中点。求证：MN⊥BD。

分析：这道题目总给人一种很突兀的感觉，不知道该如何下手。其原因在于找不出MN与BD有何联系。其实，如何下手无非两个方向：要么从已知条件出发，挖掘更多的隐藏条件为证明问题铺路；要么从求证出发，不断转化所证问题，最终将问题转化为已知条件。

方向一：从已知条件出发。

题目里有什么特殊的图形呢？

9 0º Rt△ABC和Rt△ADC，AC是它们的公共斜边；

中 点M 斜边上中点，

M B、MD是斜边上的中线， MB=MD 等腰△BDM；

中点N MN是底边上的中线，由等腰三角形的三线合一可得垂直关系。

方向二：从求证出发。

如果MN⊥BD，将有什么特殊的图形出现呢？中点，别忘了N是BD的中点！这样一来，MN就是BD的垂直平分线，那么应该有MB=MD。反过来，如果MB=MD，MN就是BD的垂直平分线。所以，问题变成了求证MB=MD。MB和MD为何相等呢，这两条线段又有什么特殊呢？由90º和中点可以得到Rt△和斜边上的中线，问题基本解决。

小结：不管从已知条件出发还是从求证出发，发现斜边上的中线是解题的关键所在。图形中没有连接MB和MD，斜边上的中线无踪无迹， MN与BD显得孤立无援。当我们连接MB、MD之后，犹豫长江两岸一桥飞架南北，天堑变通途。这就启发我们，不但要睁大眼睛寻找特殊图形，还要张开翅膀大胆想象，构造特殊图形。当我们不断地反复地咀嚼那些特殊图形，总会有灵光一闪、矛塞顿开的一刻，思维的源泉因此而欢快流畅。

特殊图形就是题目的玄机所在，找到了它我们就可以顺利、简洁地解题，所以我们应该对特殊图形保持着一种敏感，解题的灵感往往就是因为特殊图形而触发。

3