华南师范大学 广东省广州市 510631
摘要:
数学建模活动已成为高中阶段数学课程不可或缺的内容之一。本文基于数学建模的过程,设计了一个求解成卷材料长度的模型,给出了一些对数学建模活动的教学思考。
关键词:数学建模;数学课程;成卷材料长度模型
引言
在《普通高中数学课程标准(2017年版)》中,课程内容突出四条主线,“数学建模活动与数学探究活动”是其中之一,必修6个课时,选择性必修4个课时,是中国课程发展中的首次将数学建模列入到必修内容。在普通高中数学教科书(新人教A版)中,分别含有两个“数学建模”的栏目,分别为:必修第一册中的“建立函数模型解决实际问题”,以及选择性必修第三册中的“建立统计模型进行预测”[2]。在这样的背景下,数学建模活动在高中数学知识的教学中必将成为大众关注的焦点。许多学者以及一线教师都对高中数学建模的教学内容、教学实施等进行了研究和实践,也对于高中数学建模的起步和摸索提供了一定的经验。
1 案例分析
(一)观察实际情境,发现和提出问题
纸卷、布卷、磁带、油毡卷等物品是日常生活中常见的,通过测量工具可以很方便的测出它们外壳的长度、宽度,但是对于它们的长度,却不易直接去测量。那么从具体问题出发探究,对于成卷材料怎样去求它的长度?如果铜片绕在盘上,那么满盘时一盘铜片有多长呢?
(二)建立模型,求解模型
1.分析问题
对铜片侧面图进行简化,得到如下图4左侧的截面图。由于铜片厚度较薄,为0.1毫米,故可以把缠绕在绕片盘上的铜片近似看成一组同心圆。从简化图形中,可以看出,如果要求成卷物品的长度,即是需要求解一组同心圆的周长之和。为了求出一个圆的周长,则需要知道其半径,因此,在前期准备工作中需要对同心圆的半径进行测量,其中第1圈半径为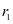 ,第2圈半径为
,第2圈半径为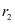 ,依次类推。而从其侧面图看,每增加一圈铜片,半径也会增加一个铜片的厚度,故需要对铜片的厚度(
,依次类推。而从其侧面图看,每增加一圈铜片,半径也会增加一个铜片的厚度,故需要对铜片的厚度(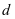 )进行测量。
)进行测量。
2.收集数据、计算数据
用千分尺量测量相关长度,并收集数据。空盘时,盘芯的直径为80毫米,即空盘时盘芯半径为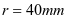 ;满盘时,直径为160毫米,即满盘时半径为
;满盘时,直径为160毫米,即满盘时半径为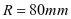 .铜片厚度
.铜片厚度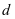 经测量得到为0.1毫米,即
经测量得到为0.1毫米,即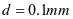 。
。
因为铜片有厚度0.1毫米,所以接下来按照厚度的中心线计算各圈的长度(单位:毫米)。
表1 铜片相关数据计算列表
圈数 | 半径 | 长度 |
| | |
| | |
| | |
| | |
| | |
3.建立模型,求解模型
通过表1可以看到,各圈长度形成一个等差数列,可以用等差数列求和公式求出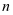 圈的总长度
圈的总长度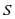 是
是
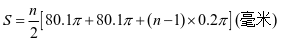 ,
,
即
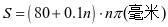 . ①
. ①
(等差数列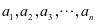 共
共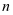 项的和
项的和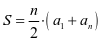 .)
.)
空盘时直径80毫米,满盘时直径160毫米,即增加了80毫米。因为铜片的厚度是0.1毫米,所以每绕一圈,盘的直径增加0.2毫米,因此,从空盘到满盘,铜片一共所绕的圈数是
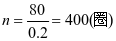 .
.
将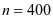 代入式子①,就得到满盘时的总长度是
代入式子①,就得到满盘时的总长度是
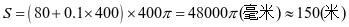 .
.
所以可以通过上面的实例,建立求解成卷材料长度的模型:
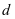 为成卷材料厚度,
为成卷材料厚度,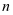 为成卷材料一共所绕圈数,
为成卷材料一共所绕圈数,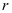 为材料空心时的盘芯的半径,
为材料空心时的盘芯的半径,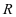 为材料满盘时的半径,
为材料满盘时的半径,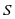 为满盘时总长度。(注意:按照厚度的中心线计算各圈的长度)
为满盘时总长度。(注意:按照厚度的中心线计算各圈的长度)
材料第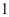 圈长度:
圈长度:
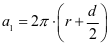
材料第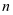 圈长度:
圈长度:
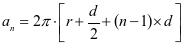 .
.
材料圈数:
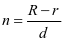 .
.
故,材料满盘时总长度有:
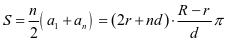 ,
,
即
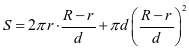 . ②
. ②
至此,最终得到了成卷材料长度的数学模型。
(三)检验结果
在这一环节中,可以用已知长度的铜片绕回空盘芯中,记录绕完铜片后所需要的圈数,通过上述模型求解绕好后的半径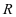 (通过式子②变形得到):
(通过式子②变形得到):
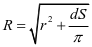
再去测量铜片实际绕好时的半径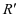 ,比较
,比较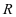 与
与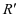 ,若两者相差较小(存在一定误差可能是由于测量过程中产生的误差,或是材料自身的材质导致的厚度不平均等问题),可以认为该模型是稳健的,否则,可以认为模型出错,需要重新建模。除了用
,若两者相差较小(存在一定误差可能是由于测量过程中产生的误差,或是材料自身的材质导致的厚度不平均等问题),可以认为该模型是稳健的,否则,可以认为模型出错,需要重新建模。除了用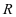 来检验模型是否稳健,也可以通过其他的变量来检验模型。
来检验模型是否稳健,也可以通过其他的变量来检验模型。
除此之外,还可以借助其他成卷的物品来检验模型,例如卷纸、涂改带、录音带等。
(四)得出模型
经过上述环节,最终得出成卷材料长度模型为:
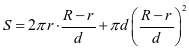
其中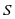 为满盘时总长度,
为满盘时总长度,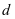 为成卷材料厚度,
为成卷材料厚度, 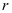 为材料空芯时的盘芯的半径,
为材料空芯时的盘芯的半径,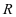 为材料满盘时的半径。即若想知道成卷材料的长度,只需测量空芯时的半径,满盘时的半径,以及材料厚度即可。
为材料满盘时的半径。即若想知道成卷材料的长度,只需测量空芯时的半径,满盘时的半径,以及材料厚度即可。
2 数学建模活动融入课堂的一些思考
(一)将高考真题与数学建模教学相互融合
近年来高考创新题型逐渐成为大众关注的焦点,而数学建模则是融入到这些题目中的一种重要的数学学科素养,所以高考试题或模拟试题中与数学建模素养相关的题目是能与数学建模教学相互结合的。这需要教师有良好的专业知识,将有关的高考试题与模拟试题进行整理、编制成学习资料,并把这些文字形式的知识转化为学生易于接受的课堂内容,让学生体验新题型,体验数学建模的魅力。
(二)发挥数学建模活动在教学中的作用
数学建模教学不仅是可以以实践活动的形式融入到教学活动中,还可以将数学建模教学有机地融入于数学解答题教学中。以真实情境为背景,教师可以编制问题驱动下的数学建模问题,这些问题可以是一种将“发现问题→提出问题→分析问题→解决问题”的培养模式,转化为“面对问题→分析问题→解决问题”的培养模式[9],有利于让学生在不知不觉中体会到数学知识及数学思维的应用,也可以进一步培养学生对现实问题进行数学抽象、用数学语言表达问题、用数学方法构建模型解决问题的数学素养。
(三)数学建模活动的开展
数学建模活动主要可以以两种形式进行开展。一种是教师结合高考知识点,问题驱动下的数学建模活动教学,并在数学建模活动后,结合高考试题中与该知识点有关的数学建模类题目进行讲解分析,以应对近些年来的高考新题型考查。另外一种是鼓励学生在课后,以小组为单位,结合实际生活中可能会遇到的与数学建模相关的问题,进行数学建模活动。若将以上两种数学建模活动相结合,则可以实现第二点中提出的两种培养模式。
参考文献
[1]章建跃,张艳娇,金克勤.数学建模活动的课程理解、教材设计与教学实施[J].中学数学教学参考,2020(13):13-19.
[2]章建跃,张艳娇,金克勤.数学建模活动的课程理解、教材设计与教学实施(续)[J].中学数学教学参考,2020(16):13-16+31.