弹簧类问题初探

弹簧类问题初探

武锦花

山西省晋中市祁县中学 山西 晋中 030900

摘要：对于弹簧，从受力角度看，弹簧的弹力是变力；从能量角度看，弹簧是个储能元件。因此，弹簧问题能很好地考查学生的综合分析能力，学生在解题过程中也常出现问题，故备受高考命题者的青睐．

高中物理中涉及弹簧的问题是较多的，学生的答题情况不容乐观，出现很多问题，错误率较高。我认为有两方面的原因，一是没有掌握弹簧类问题的规律方法，缺乏信心，硬着头皮，稀里糊涂地做，，二是确实题的难度较大，涉及到的知识综合性强，做不出来。所以，探讨一下关于“弹簧类”问题蛮有必要。结合高考题大致有下列几方面问题。

1、弹簧的瞬时问题

弹簧的两端都有其他物体或力的约束时，使其发生形变时，弹力不能由某一值突变为零或由零突变为某一值。

2、弹簧的平衡问题

这类题常以单一的问题出现，涉及到的知识是胡克定律，一般用f=kx或△f=k•△x来求解。

3、弹簧的非平衡问题（临界或振动问题常见）

这类题主要指弹簧在相对位置发生变化时，所引起的力、加速度、速度、功能和合外力等其它物理量发生变化的情况。要注意变化的外力存在极值问题。尤弹其注意合力为零或者簧恢复原长的位置。

4、 弹力做功与动量、能量的综合问题

在弹力做功的过程中弹力是个变力，并与动量、能量联系，一般以综合题出现。有机地将动量守恒、机械能守恒、功能关系和能量转化结合在一起。分析解决这类问题时，要细致分析弹簧的动态过程，利用动能定理和功能关系等知识解题。W=KX²/2

弹簧的瞬时问题

例1.（2001年上海）如图（A）所示，一质量为m的物体系于长度分别为l1、l2的两根细线上，l1的一端悬挂在天花板上，与竖直方向夹角为θ，l2水平拉直，物体处于平衡状态.现将l2线剪断，求剪断瞬时物体的加速度.

2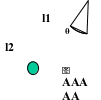 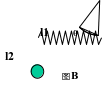.若将图A中的细线l1改为长度相同、质量不计的轻弹簧，如图（B）所示，其他条件不变，求剪断瞬时物体的加速度.

分析：我们讨论的弹簧都是轻质弹簧，即不考虑弹簧的质量，且认为弹簧两端的弹力大小一样，否则的话，轻弹簧的加速度很大。对于两端接有物体的弹簧，它的形变发生改变的过程因两端物体的惯性而需时较长，在很短的时间内形变量可认为是不变的，因弹簧的弹力由形变决定，即在很短的时间内认为弹簧的弹力是不变的；但一端如果因失去物体而作用力消失，那么另一端的作用力也必将消失。

平衡问题：

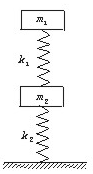
例2.如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，上面木块压在上面的弹簧上（但不拴接），整个系统处于平衡状态.现缓慢向上提上面的木块，直到它刚离开上面弹簧.在这过程中下面木块移动的距离为( )

A m₁g/k₁ B．m₂g/k₁

3. m₁g/k₂ D．m₂g/k₂

分析：在共点力作用下物体的平衡条件是物体所受的合外力为零，但如果涉及到弹簧，那么就得多考虑一个因素——弹簧的弹力与弹簧的伸长量（或压缩量）有关系。弹簧形变量的变化量就是物体移动的位移。同压缩（同拉长）位移为两形变量之差，拉长变到压缩或压缩变拉长位移为形变量之和。

临界问题：

例3 （2005年全国理综III卷）如图所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量分别为mA、mB，弹簧的劲度系数为k,C为一固定挡板。系统处一静止状态，现开始用一恒力F沿斜面方向拉物块A使之向上运动，求物块B刚要离开C时物块A的加速度a和从开始到此时物块A的位移d，重力加速度为g。

分析：弹簧连续形变其弹力为变力，在弹簧作用下的运动一般是加速度变化的变速运动，简谐运动只是其中的一种。如果连接弹簧的物体做匀变速，必有变化的外力作用，要注意变化的外力存在极值问题。尤弹其注意合力为零或者簧恢复原长的位置。

解：令x1表示未加F时弹簧的压缩量，由胡克定律和牛顿定律可知

令x2表示B刚要离开C时弹簧的伸长量，a表示此时A的加速度，由胡克定律和牛顿定律可知：mgsinθ=kx1 ①

kx2=mBgsinθ ②

F－mAgsinθ－kx2=mAa ③

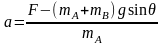
得

由题意 d=x1+x2 ⑤

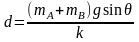
由①②⑤式可得

与振动结合问题

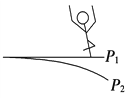
例4如图所示，跳板跳水运动员向下压跳板，随跳板一起从位置P₁运动到位置P₂，则此过程中(　)　

(A) 运动员的速度不断减小。

(B) 运动员的加速度不断变大。

3. 先是弹力做的负功小于重力做的正功，然后是弹力做的负功大于重力做的正功。

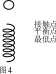( D) 到最低点时，运动员加速度的值一定大于重力加速度的值 。

解析：本题常见形式是一个球从高处下落到一支竖在地面上的弹簧的顶端（图4）。运动员下落到与跳板接触时，就相当于球下落到直立的弹簧上，我们把图4球接触弹簧后的运动划分成三个点和三个点之间的两个阶段来研究，这三个点就是接触点、平衡点和最低点。从接触点到平衡点，小球所受的重力大于弹力，加速度逐渐减小，速度逐渐增大，重力的功大于弹力的功，动能逐渐增大，重力势能逐减少，弹性势能逐渐增大；；从平衡点到最低点，小球所受的弹力大于重力，加速度逐渐增大，速度逐渐减小，重力的功小于弹力的负功，动能逐渐减少，重力势能逐渐减少，弹性势能逐渐增大。对于选项（D），把小球接触弹簧后的运动看作简谐运动，简谐运动具有对称性。最低点是简谐小度中插入文力），这三个力的全运动的一个端点，而接触点不是端点，接触点位置有速度，由于简谐运动过程中速度小处加速度大，接触点处的加速度为g，所以最低点处（端点）的加速度就大于g 。

与功能结合问题

例5. (2005年全国卷Ⅰ)如图，质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连，弹簧的劲度系数为k，A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮，一端连物体A，另一端连一轻挂钩。开始时各段绳都处于伸直状态，A上方的一段绳沿竖直方向。现在挂钩上挂一质量为m3的物体C并从静止状态释放，已知它恰好能使B离开地面但不继续上升。若将C换成另一个质量为(m1+m3)的物体D，仍从上述初始位置由静止状态释放，则这次B刚离地时D的速度的大小是多少？已知重力加速度为g。

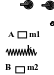
分析：弹力做功是一个“变力”做功的问题，在中学物理中，“变力”做功应用动能定理来解答，弹性势能在中学物理中没有定义式，在求其值的时候，必须应用能量守恒的原理来求，对于较综合的题型，虽然先后涉及到几个较复杂的过程，但往往会出现先后二个状态弹簧的形变情况一样，这就意味着先后二个状态弹簧的弹性势能一样，对此必须引起足够的重视。

解析：先后两个状态都讲到B刚要离开地面，即弹簧的弹力都等于m₂g，即先后讲到的B要离开地面的两个状态对应的弹簧弹性势能相等，由于初态的弹性势能一样，可见弹性势能的改变量E相等。

初态：弹簧的压缩量x₁ = m₁ g/ k

B刚要离开地面时弹簧的伸长量x₂= m₂g/k₂

第一过程E= m₃g（x₁ +x₂）－m₁ g（x₁ +x₂）

第二过程E=（m₁+ m₃）g（x₁ +x₂）－m₁ g（x₁ +x₂）－（m₁+ m₃）v²－m₁v²

解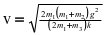 得

学生的认知水平和科学思维都是在应用知识，方法解决物理问题中不断发展的，只要不断总结，学生解决问题的能力就会不断提升，思维会越来越敏捷，解题速度和准确率会大大提高。