如何讲授《二次函数》

如何讲授《 二次函数》

马雪

黑龙江省桦川县横头山镇中学 154300

摘要：二次函数是人教版初三年级上学期第二十三章内容。这章设置在初三的开端不仅体现了它的重要性，也体现了初中阶段由初二过渡到初三的关键期，无疑，二次函数是初中阶段较重要较困难的一章，在之前已经学习了《一次函数》同学们对函数有了初步的认识，但由《一次》过渡到《二次》难度也是成倍增长的。那么如何讲授这章内容呢？如何能让同学们快速掌握那，下面说说我的几点看法。

关键词：二次函数;数学竞赛;教师辅导

《二次函数》在多年来都成为教师较为头疼的一章，学生也因“变化”而对函数望而生畏。教师也因不能由浅显易懂的切入点将“变化”讲授给学生而苦恼。我觉得原因主要有两点，一、学生在认识上的转变。在初一，初二阶段，多数知识点都是固定不变的，具有固定答案的。而二次函数是由多对连续且变化的点组成的曲线，同时也无法将图与式子建立联系而困惑。二、教师站在已有知识的高度去讲授，不能从初学者，且思维发展还不是很全面的角度去研究这章内容。

那针对这样的情况我是这样做的。首先在给函数下定义时要联系与一元二次方程的关系。用类比的思想，先回顾一次函数以及一元一次方程的关系。先让学生在思想上放轻松，从而给二次函数下定义时，就可以利用类比记忆。并且说明一次函数与二次函数的不同点及相同点。再次要讲清几种二次函数的形式，由基础式入手，研究其图像找到顶点坐标，对称轴以及最值与y=ax²的联系。a是确定开口方向以及大小的。再由移动顶点从而引出顶点式，同样要研究顶点坐标，对称轴及最值，更重要的是要与基础式做比较。清楚基础式其实也是顶点式的一种特殊形式。再回归到一般式讲清一般式与顶点式的关系，虽然形式不同，但都可以表示同一种函数，它们是可以互相转化的。对这两种形式进行说明，一般是可以直观的认识到a是决定抛物线开口方向以及大小的。而a和b决定了对称轴与y轴的位置。例如左同右异a与b同号对称轴在y轴左侧，异号对称轴在y轴右侧。c决定抛物线与y轴的交点，而顶点式中a也决定开口方向，并且可以直观确定顶点的位置，直接找到其最值。要着重理解几种形式间的关系。例如1.y=ax²向左右移动h个单位长度。可以得到y=a(x-h)²。2.y=ax²向上或者是向下移动k个单位长度。可以得到y=ax²+k。这里可以利用顺口溜左加右减纵不变，上加下减，横不变。3.那么顶点式y=a(x-h)²+k是由y=ax²向上下移动k个单位长度向左右移动h个单位长度得到的。4.根据一元二次方程的关系说明，函数图像与x轴有两个交点时，可以用两根式。两根式y=a(x-x₁)(x-x₂)这种形式是抛物线与x轴有两个交点(x₁，0)（x₂，0）这种形式可以快速找到对称轴，并且还可以根据这函数解析式。快速找到与X轴的两个交点坐标。例如基础式y=4x²，其顶点坐标为（0，0）。对称轴便是x=0，也就是y轴。当x=零时，y有最小值。Y=4x²+1，顶点坐标是(0，1)。对称轴是x=0，当x=0的时候，y有最小值1。Y=（x-1）²，其顶点坐标为(1，0)，对称轴为x=1。当x=0时，y有最小值1;y=4(x-1)²+1顶点坐标为（1，1）。对称轴是x=1，当x=1时，y有最小值1。而一般式y=ax²+bx+c，其顶点坐标为(-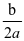 , 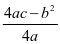)，就可以找到对称轴，以及最值，只要将规律弄清楚，就可以将二次函数灵活掌握，并且知道它的顶点坐标，对称轴，以及当对称轴为多少时y有最值。

接着二次函数这章较为重要的就是利用待定系数法来求二次函数的解析式，同样只要掌握几种类型，就能轻松掌握。若题目中出现抛物线，经过a点b点c点已知的三点。那么就可以利用将三点带入一般式y=ax²+bx+c得到abc的值，得到顶点坐标，对称轴以及最值；若出现抛物线经过顶点a以及点b就可以利用，将两点代入顶点式y=a(x-h)²+k。若出现抛物线与x轴交于两点，x₁，x₂以及任意一点A就可以用两根式来求得。那学习二次函数比较重要的就是要了解它的函数解析式是什么样的，它的图像是什么样的。根据式的不同，来选择不同的解法。要根据给的点的坐标，由哪些特点来选择，适当的解析式的形式。

那对二次函数有了一定的基础，并且已经掌握了一些知识，那接下来我们要学习的就是二次函数的应用，通常会与一次函数，三角形和平行四边形综合出题，这里就要注意以下几点，将两个函数联立起来，就可以求得交点的坐标，要从学会设点的坐标，直接设或者是间接设来入手，例如,当点p在抛物线y=x²+2上。那么就可以设p的坐标为(t,t²+2);若题目中说点Q在x轴上,过Q可以做PQ垂直x轴于点Q。过P做抛物线y=x²+3那Q点坐标为(t,0)那么设p点坐标就是(t,t²+2)。在平面直角坐标系中会求得线段的长，只要有两点坐标就可以求得线段的长度，例如，a点坐标为(1,2)，b点坐标为(1,3)，那么线段AB就等于2，他们的纵坐标相减，横坐标不变。A点坐标为（2,0）,B点坐标为(4,0)。那么ab线段就等于2。只需将横坐标相减，斜线段的求法通常可以构造直角三角形，利用勾股定理来求得，从而得到线段AB。那么两点间距离公式

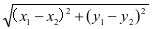.由点到线段再到三角形的面积，四边形的面积。这是二次函数中比较重要的过渡。

那学习在平面直角坐标系中求三角形的面积，四边形的面积时，就要利用函数解析式或者勾股定理。当三角形一边平行或垂直于x轴时，三角形的底边很容易求得，那么高，如何求得呢？这就是我们这里的重点以及难点底边所对的顶点向底边做垂线，用公式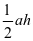 来求得三角形的面积。例如当三角形AOB在三角形平面直角坐标系中，A点的坐标为（3,2）b点的坐标为（4,0），那么它的面积就是1/2×4×3=6。,那如果一个三角形没有一条边平行于x轴或者是垂直于x轴，我们就要运用补形法或者是切割法来求得三角形的面积，就是先求出三角形所在区域的矩形的面积，然后减去它周围的三个三角形的面积，从而求得。例如，当a点坐标为（1,3）B点坐标（5,3）c点坐标（3,0）时。要想求得三角形ABC的面积，就要先求得四边形的面积，从而减去三个三角形的面积得到，也可以用切割法，用函数的知识来求。那么就要需要做BD垂直AC求出AC的函数解析式，那么就能得到直线BD函数解析式的k值，再将B点代入就能求得BD的函数解析式，连BAC和直线CD，那么就可以得到D点的坐标。知道D点的坐标B点的坐标，知道带入两点间距离公式就可以得到BD的长度，a点坐标c点坐标。同样可以得到ac的长度，这样1/2底乘高就求得了三角形ABC的面积。

总体看来，二次函数是初中的重点以及难点，但是他的学习是循序渐进的。所以在讲授的时候，一定要从基础入手。先将几种基础的函数解析式弄清楚,然后熟悉图像。这就是我对这一章《二次函数》的学习的一些建议和方法。

参考文献：

[1]如夫. 二次函数的应用.教育学,2005-12.

[2]二次函数（二）.教育学,2010-03.

[3]二次函数（二）.教育学,2009-06.