等比数列概念 教学设计

等比数列概念 教学设计

陈洪卫

贵州省仁怀市第一中学 564500

摘要：本文主要探究等比数列概念的教学设计措施。

关键词：等比数列概念；教学设计

前言：

在新课程目标中，要求教学活动以智力参与为前提，以学生为主体为基础，以个人体验为终结。在学生学习中，不仅仅需要教师从外向内为学生传递知识，还需要学生能够自主选择加工，主动改造、通过新旧知识相互作用，充实现有知识经验，形成新认知经验。本文主要以等比数列概念为例，分析教学设计措施，从而加强学生对知识的理解。

1教学分析

1.1教材分析

高中教学中，数列作为重要内容，是离散现象刻画的函数，其作为重要数学模型，具有承上启下作用。教学内容及过程为学生核心素养发展提供生长点，以数学语言进行数列描述，构建等比数列概念，可培养学生抽象数学思维。

1.2学情分析

高一学生拥有一定推理、概括、分析及理解能力，初步形成逻辑思维能力，但受到年龄制约，尽管思维较为敏捷活跃，却也缺乏深刻和冷静，问题思考存在不严谨，片面情况。学生对等比数列具有一定认知，对数列公式和方程应用技能不透彻、不全面。

2教学目标

一般目标：通过生活实例，使学生掌握等比数列概念，能够通过概念证明和判断等比数列，面对具体情境问题，发现数列等比关系，利用知识解决问题。在教学中，坚持问题导向，开展观察、运算、抽象、推理、验证等活动，设置问题情境，以促进学生形成和发展数学核心素养，培养其勇于探索的学习方法与积极思考的学习习惯，增强数学应用意识，个性品质上激发学习兴趣。

教学重点：掌握等比数列概念，体会等比数列自然规律，采取类比、归纳等方式解决实际问题。

教学难点：深刻理解等比数列通项公式与定义，探索具体问题情境，利用概念与公式实现新问题解决。

3教学过程

3.1新课导入

教师在课堂上通过新媒体为学生展示图片（见图1）。

图1 7层蛋糕塔

师：这个蛋糕塔一共有7层，每一层蛋糕均为圆形，蛋糕最上层半径为8cm，第2层半径12cm，以此类推，每一层蛋糕塔半径相较于上一层的半径均多出4cm，那么最下面的蛋糕半径是多少？

生：32cm。

师：同学们都回答的很好，最后一层蛋糕为32cm，在解答过程中，我们主要应用了哪些知识呢？

生：等差数列。

师：那同学们还记得等差数列概念及其通项公式吗？

生：记得！（回答概念与通项公式）

设计意图：传统教学中通常为教师提问、学生回答，此种模式无法达到良好效果。而采取情境设置的方式，利用图片信息吸引学生注意，设置学习情景，进而引导学生了解学习目标，能够将数学信息直观、刺激的呈现到学生面前，以激发其数学学习兴趣，启迪思维，调动学生发现与和好奇心。

3.2探究新知

师：类比等差数列和项之间关系，同学们还能想到其他特殊数列吗？请举出例子，小组之间交流讨论。

学生先通过独立思考，之后在小组交流中将思考内容列出，写出独特列式。

生1：有1、1、1、1、1、1、…

生2：有1、2、4、8、16、…

生3：有1、2、1、2、1、2、…

生4：有1、2、3、5、8、13、…

生5：有1、-1、1、-1、1、…

生6：有1、3、9、27、81、…

师：根据上述列式，你能发现它们有哪些特征，给它们起个名字吧！通过小组讨论方式，学生概括上述列式特点。

生1：a₁=a₂=a₃…，为常数列，即等差数列。

生2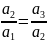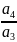： = …，为等比数列。

生3：a₁*a₂₌a₂*a₃…，称为等和数列，即等积数列。

生4：a₁+a₂=a₃,a₂+a₃=a₄,…，通过课前预习，了解其为斐波那契数列。

生5：a₁+a₂=a₂+a₃=a₃+a₄…，为等和数列，等比数列、等积数列。

生6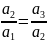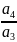： = …，为等比数列。

师：在以上数列中，我们已经研究过等差数列，等积数列等内容明确，较为简单，今天让我们共同了解等比数列，其内容丰富，研究价值较高。

设计意图：让学生在回顾等差数列得知识点后，通过“你能够想到其他特殊数列”的方式，引发学生想象与联想，鼓励学生从“运算”层面思考，从数学内部引出新概念，以辨析、比较的方式，揭示“等比数列”研究必要性与合理性。并且，采取小组讨论合作方式，可构建讨论“局域网”，实现相互启发，推动学生参与到新概念学习中。

3.3推导分析

师：等比数列相较于等差数列，具有哪些特点？

生：可以了解等比数列的项，从第2项开始，之后每一项都是前一项2倍。

师：这就是我们研究的等比数列，学习等比数列的概念。请同学们结合等差数列概念与等比数列特点，看看哪个小组能够迅速归纳等比数列概念特点？并能用数学语言准确表达这等比数列的概念。

给出列式：1/2、2、8、32、128、…

提问：这是什么数列？公比q为多少？数列第n项是什么？

设计意图：引导学生类比推导出等比数列通项公式。在电脑上利用PPT展示该数学思维过程，使得学生能够探索详细过程，引导学生猜想、分析、验证，以归纳等比数列通式，不仅可帮助学生掌握公式，还能为后续使用等比数列解题奠定基础。

3.4应用概念

例题1：（1）-4、b、c、1/2；（2）2、a、8。求出等比数列未知项。

例题2：数列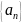 中，任意正整数n（≥2），均有 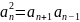，则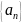 一定为等比数列吗？

设计意图：通过探究练习，使学生回到概念定义中，应用概念及变式解决问题，加深学生列概念能力，进而实现概念活化应用，让概念成为学生观念，成为问题解决的经验与工具。

4教学反思

教学内容在于发展学生核心素养，数学学习中，素材作为重要资源，理解教学内容，吃透教材有助于教师通过教学设计落实核心素养，为教学提供着力点。而等差数列由于和等比数列相似点较多，等比数列概念教学中，可采取类比归纳方式，以等差数列为导入的旧知识点，建立等比数列概念，明确等比数列与等差数列内在联系。并且，课堂中将主动权给学生，让学生自己反思，如“你还能想到其他特殊数列吗”，设计开放性和思想性问题，吸引学生思考，给出自身答案，提高学生求知欲。同时，通过一连串问题展开“小组合作”，建立“微型学习共同体”，围绕概念、特点等进行辨析讨论，学生能够主动积极参与其中，让课堂绽放出智慧火花。

参考文献：

[1]杨瑞强.基于核心素养的数学单元教学设计初探——以“数列”的教学为例[J].中小学数学(高中版),2020(05):5-8.

[2]陈平.基于发展核心素养的概念课教学设计——以“等比数列”教学为例[J].中学数学研究,2020(04):4-8.

[3]赵亚娟.基于等比数列递增的线性WSNs网络部署方案[J].中国电子科学研究院学报,2018,13(04):389-393.

[4]柴有茂.核心素养引领下的“等比数列”教学设计[J].当代教育与文化,2018,10(03):85-88.