中国民航大学 天津 300300
摘要 为了减少无人机飞行控制训练中外界因素的影响,降低无人机的试飞成本,设计一款飞行操控仿真训练系统。综合运用Matlab/Simulink、FlightGear等仿真工具,以虚拟现实方式对无人机模型、持控系统、环境实景等进行仿真,实现安全、高效、低耗的模拟飞行训练。
关键词 无人机;飞行控制仿真;模拟训练系统
0 绪论
无人机 (UAV)体积小、重量轻、机动性好、使用维护方便[1]。现阶段,国内外无人机都迎来了大发展,有着很大的发展潜力和良好的应用前景。我国在航空航天等领域的半实物仿真技术方面已成功建设了一批大规模、高水平的实物成果。随着科技水平的进步以及国家实力的增强,半实物仿真技术也取得了长足的进步[2]。
不过无人机作业人才培养的模式还存在一些缺陷,无人机的飞行训练往往受场地、天气、备件、燃料等因素影响,尤其新手训练时极易因操控熟练度问题造成安全事故,危及人员和财产安全。
针对这种情况,课题设计一款无人机操控模拟训练系统,基于目前已有的MATLAB/Simulink RTW 接口集成技术,以虚拟现实方式对无人机模型、操控、环境实景等进行仿真,以“真实性”和“互动性”为设计理念实现操控反馈、数据通信及过程训练,可有效提高学习训练效率,提高受训人员的专业素质,同时也降低了训练成本和无人机损耗,减少了危及人员和财产安全事故的发生[3]。同时该系统还可用于无人机飞行规律研究、性能评估、飞控系统的仿真测试等场景,因此具备较强的研究意义与应用价值。
1系统总体结构概述
该无人机飞行控制仿真模拟系统主要包括持控系统,无人机模型和环境实景构建三个板块,系统结构如图1所示。以下描述各模块的作用及相互间的关系。
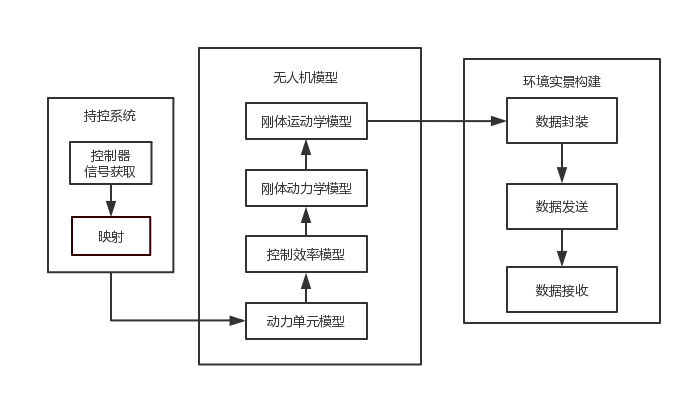
图1 系统结构
(1)持控系统分为外接控制器信号获取和信号映射两部分,利用Matlab Simulink提供的模块获取外接控制器的操作信号,处理后模拟为无人机控制器的通道输入信号,再在映射中将其转换为对无人机电机的指令信号,传递至无人机模型板块。
(2)无人机模型板块由动力单元,控制效率,刚体动力学,刚体运动学四个模型组成,接收持控系统传来的油门指令,通过四个模型依次进行运算将油门的数据最终转化成无人机的位置和姿态信息传递给下一板块。
(3)将无人机位置、姿态等基本信息按环境实景软件要求格式进行封装处理,设置发送端和软件接收端参数建立网络通信,将数据发送至实景软件端产生仿真图像。
2实时飞行仿真模块设计与实现
2.1无人机模型
2.1.1无人机的选取
市面上常见的无人机类型有三种,分别是固定翼、直升机和多旋翼。对于仿真系统的设计来说,理想化了模型,减少了一些因素影响,例如电池电量的情况对飞行时间的影响。所以重视的性能是无人机的易用性和可靠性。固定翼无人机但起飞必须要助跑或者弹射助力,降落也需要跑道滑行,这对于环境要求较高,易用性上的体验极差[4]。直升机类型能够垂直起降,但自身的物理结构复杂、维护成本高不适用于非专业用户。而多旋翼无人机能够不受起点环境限制垂直起降,且结构简单易于维护,虽然载重和续航能力相对较差,但对于仿真系统的开发并无影响。综上比较, 决定采用结构简单、模块化的四旋翼无人机进行模拟。
通过对比常见无人机的参数和性能,权衡后最终选取了重量为1.4kg,轴距450mm的F450四旋翼无人机,并通过simulink进行动力系统建模。
2.1.2参数定义
表1 动力器件参数
器件 | 参数指标 |
螺旋桨 | Θp={直径Dp=6mm,螺距HP=11mm,桨叶数Bp=4,重量Gp=20g} |
电机 | Θm={标称空载值KV0=1500kv,最大电流ImMax=16A,标准空载电流Im0=0.7A,内阻Rm=95mΩ,重量Gm=46g} |
电调 | Θe={最大电流IeMax=60A,持续电流Ie=40A,重量Ge=26g} |
电池 | Θb={总容量Cb=25C,内阻Rb,总电压Ub=11.1V,最大放电倍率Kb=2200mAh,重量Gb=196g} |
表2 无人机各项指标参数
无人机定量名称 | 参数 | 参数值 |
无人机总质量 | m | 1.4(kg) |
重力加速度 | g | 9.8(m/s²) |
转动惯量矩阵 | Jxx | 1.349e-2(kg.m²) |
Jyy | 1.349e-2(kg.m²) | |
Jzz | 2.352e-2(kg.m²) | |
机身半径(1/2轴距) | d | 0.225 (m) |
单桨综合拉力系数 | Ct | 8.102e-6(N/(rad/s)²) |
单桨综合力矩系数 | Cm | 1.051e-7(N.m/(rad/s)²) |
电机曲线 | CR | 747.44(rad/s) |
电机螺旋桨转动惯量 | Jm | 5.60e-5(kg.m²) |
电机响应时间常数 | Tm | 0.0176(s) |
机身阻力系数 | Cd | 0.06579(N/(m/s)²) |
机身阻尼力矩系数 | Cdm | 9.012e-3 N.m/(rad/s)² |
2.2动态模型的建立
2.2.1坐标系的定义
地球坐标系oexeyeze用于研究无人机相对于地面的运动状态,确定机体的位置,忽略地球曲率。将起飞位置作为坐标原点oe,让oexe轴在水平面内指向一方向,oeze轴垂直于地面向下。按照右手定则,右手拇指指向oexe轴,中指指向oeze,食指指向oeye轴。
机体坐标系obxbybzb与无人机机体固连,原点ob取在多旋翼的重心位置,obxb轴在无人机对称平面内指向机头方向。Obzb轴在无人机对称平面内,垂直obzb轴向下。按照右手定则,右手拇指指向obxb轴,中指指向obzb,食指指向obyb轴。
定义如下单位向量:
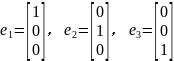
在地球坐标系下,沿oexe、oeye和oeze轴的单位向量分别表示e1,e2,e3。在机体坐标系下,沿obxb,obyb和obzb轴的单位向量满足如下关系:bb1=e1,bb2=e2,bb3=e3,在地球坐标系下,沿obxb、obyb和obzb轴的单位向量分别表示eb1,eb2,eb3[5]。
2.2.2姿态表示
(1)欧拉角定义:根据欧拉定理,刚体绕固定点的旋转可以堪称绕该点的若干次有限旋转的合成。地球坐标系统固定点经过三次基本旋转,可以得到机体坐标系。在这三次基本旋转中,旋转轴是待转动坐标系的某一对应坐标轴,旋转角度即为欧拉角。因此,字条矩阵可以用三次基本旋转矩阵的乘积表示。直观地,令地球坐标系与机体坐标系完全一致,则定义偏航角、俯仰角和滚转角。偏航角Ψ为机体轴为obxb在地面上的投影与地轴oexe间的夹角(规定机体向右偏航时角度为正),俯仰角θ为机体轴obxb与地平面间的夹角(规定机体头部上扬时角度为正),滚转角Φ为机体轴obyb与地轴oeye之间的夹角(规定机体向右滚转时角度为正)
(2)姿态变化率与机体角速度关系:
如果机体旋转角速度为
b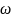 =[
=[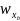
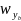
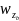 ]T,
]T,
那么姿态变化率与机体旋转角速度有如下关系,
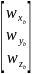 =
=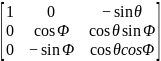 =
=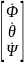
则
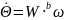
其中
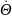 =
=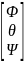 ,W=
,W=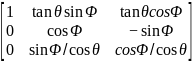
2.3无人机的控制模型
2.3.1关于无人机的几个假设
为了简便动力系统建模,作出以下几个假设:
假设1.无人机是刚体;
假设2.质量和转动惯量是不变的;
假设3.无人机的几何中心与重心一致;
假设4.无人机只受重力和螺旋桨拉力,其中螺旋桨拉力沿Zb轴负方向,而重力沿Ze正方向。
2.3 2无人机控制模型
无人机控制模型的总体是由动力单元模型,控制效率模型,刚体动力学模型,刚体运动学模型这四部分组成,如图2所示。
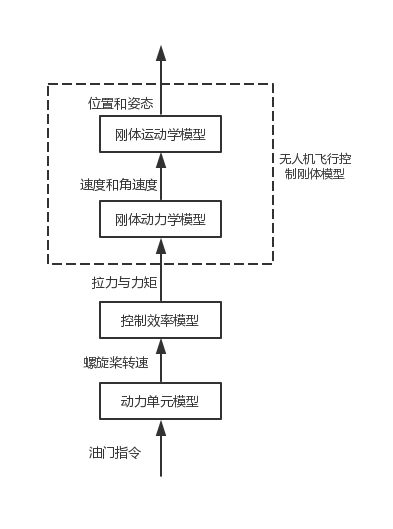
图2 无人机建模层次结构
动力单元模型是以无刷直流电机、电调和螺旋桨为一组的动力机构,如图3所示。
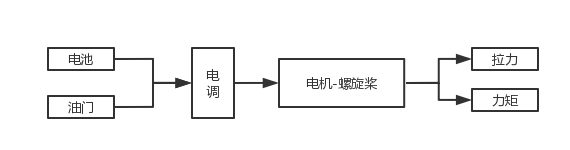
图3 动力系统信号传递图
由电池和油门输入电池电压和0到1的电机油门指令后进行电调,然后进入电机螺旋桨,其中从油门产生转速可由关系式
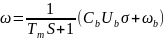
(其中σ表示油门指令的输入,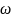 表示电机转速为输出,Ub是电池输出电压,Tm是电机动态响应的常数,
表示电机转速为输出,Ub是电池输出电压,Tm是电机动态响应的常数,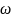 b为常数)
b为常数)
得出转速,传给下一接口计算拉力和力矩。
控制效率模型接收到上一接口传来的螺旋桨的转速,输出拉力和力矩。所研究的X字形四旋翼无人机如图4所示。
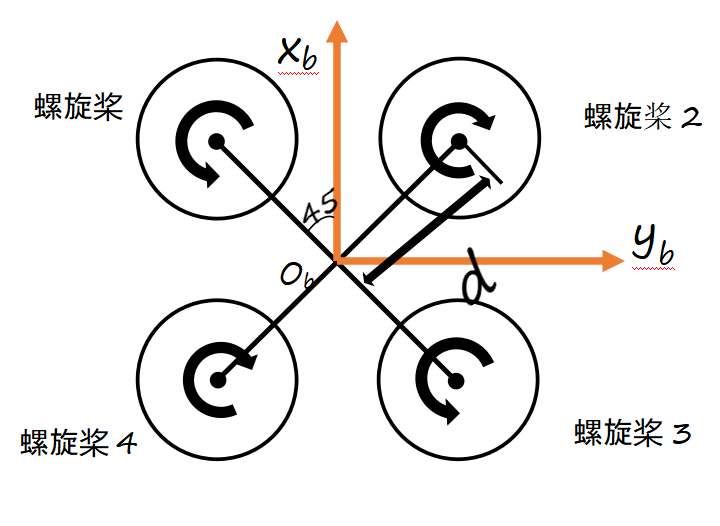
图4 X型无人机机架布局
由 f=CT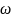 2 ,
2 ,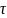 =CM
=CM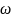 2
2
可以得到关系式:
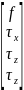 =
=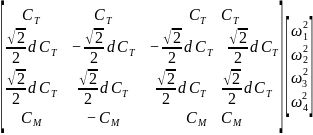
(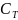 ,
,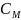 分别为拉力系数和扭矩系数,
分别为拉力系数和扭矩系数,
f是作用在机体上的总拉力,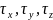 分别是螺旋桨俯仰力矩、横滚力矩和偏航力矩,
分别是螺旋桨俯仰力矩、横滚力矩和偏航力矩,
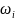 是螺旋桨i的转速)
是螺旋桨i的转速)
用此关系进行计算得到拉力和力矩传给下一接口。在这里将关系式化简,用控制器把未知参数进行补充,可得到下列关系式,
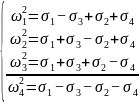
(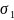 、
、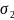 、
、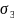 、
、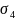 分别设为油门、俯仰、横滚和偏移四个通道的输出)
分别设为油门、俯仰、横滚和偏移四个通道的输出)
(3)刚体动力学模型接收上式计算出的拉力和力矩,转化为速度和角速度并输出。首先在假设4成立下,地球系下的位置动力学模型无人机只受重力和螺旋桨升力,它与一般刚体动力学模型是不同的。其中螺旋桨拉力沿Zb轴的负方向方向,也就是说它是垂直于机身所在的平面,重力是沿Ze方向。基于假设4:由方程
e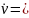 eF/m
eF/m
(m为无人机的总质量,eF为总拉力)
得到位置动力学模型,基于假设1-3,在机体坐标系下由
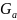 =JRP(b
=JRP(b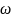 ×e3)(-1)k+1
×e3)(-1)k+1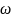 k
k
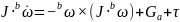
(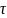 表示螺旋桨在机体轴上产生的力矩,J表示无人机的转动惯量,
表示螺旋桨在机体轴上产生的力矩,J表示无人机的转动惯量,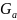 表示陀螺力矩,JRP表示整个电机转子和螺旋桨转轴的总转动惯量,b
表示陀螺力矩,JRP表示整个电机转子和螺旋桨转轴的总转动惯量,b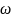 表示电动机曲线常数参数,)
表示电动机曲线常数参数,)
可以得到内姿态动力学模型。
(4)最后刚体运动学模型收到速度和角速度后,基于假设1,通过方程
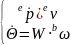
(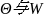 的等式在2.2 2中已经给出推理)
的等式在2.2 2中已经给出推理)
将位置和姿态信息传递给三维图像显示模块。
2.4持控系统搭建
持控系统由遥控器和控制器两部分组成。遥控器部分获取外接真实遥控器的操作将其转换为信号,控制器将遥控信号转换至无人机电机的预期信号。
2.4.1遥控器模块设计
遥控器模块的功能在于产生控制器模块需要的通道输入信号,同时要以符合现实无人机的操作逻辑来对应相应信号。本系统中只设计滚转、俯仰、油门和偏航的遥控。
该模块的期望效果为将遥控器的右摇杆上下方向推动对应控制无人机俯仰角即向前后飞行;左右方向对应控制无人机滚转角即向左右飞行;左摇杆的上下方向对应油门即无人机的升降;左右方向对应偏航控制;此外虽然本系统中以F450为研究对象在遥控时为直接式油门控制方法,不推动摇杆时摇杆固定,油门值也固定。
确认对应关系后,使用Simulink提供的JoystickInput模块接入手柄,获取手柄摇杆和按钮的信号,模拟得到最终的通道信号。
2.4.2控制器模块设计
该模块分为遥控信号处理、姿态控制、电机分配三部分,共九个输入,一个输出。
(1)输入输出情况。输入包含遥控器的四个通道输入,从1号到4号分别为油门、俯仰、滚转和偏航,还包含五个无人机状态信号,从6号到10号分别为滚转、俯仰和偏航的角速度以及滚转角和俯仰角,本系统直接取自无人机模型输出状态值。经过一系列处理后最后输出一个电机的PWM调制信号作 为下一部分无人机模型的输入信号。
(2)遥控信号处理。把来自遥控器的通道信号转换为姿态控制需要的滚转和俯仰角度。
(3)姿态控制。通过输入的期望姿态信号计算输出期望力和力矩大小,此处以图4为基础进一步解释。
a.垂直上升与下降运动
理想状态下,在竖直方向上无人机的升降取决于四个螺旋桨产生的合力F与无人机自身的重力mg的差,因此若想上升只需令四个螺旋桨的升力同时增大,反之若想下降则令四个螺旋桨的升力同时减少。
b.俯仰运动
无人机的俯仰运动是围绕y轴进行的,若想向前进即俯运动则令螺旋桨1、2的升力和小于螺旋桨3、4的升力和;反之向后运动同理。两组螺旋桨的升力和差产生的不平衡力拒会使无人机绕y轴旋转,从而实现俯仰运动,此外,为了避免运动过程中x轴方向的影响,改变每组螺旋桨升力大小时应该令两个螺旋桨改变相同的值以避免产生影响x轴的力拒。
c.滚转运动
无人机的滚转运动是围绕x轴进行的,若想向右运动则令螺旋桨2、3的升力和小于螺旋桨1、4的升力和;反之向右运动同理。两组螺旋桨的升力和差产生的不平衡力拒会使无人机绕x轴旋转,从而实现滚转运动,此外,为了避免运动过程中y轴方向的影响,改变每组螺旋桨升力大小时应该令两个螺旋桨改变相同的值以避免产生影响y轴的力拒。
d.偏航运动
螺旋桨旋转时带动周围空气运动产生扭矩,同时空气对螺旋桨反作用力也在对螺旋桨产生力拒,螺旋桨因此带着无人机机身一起旋转。在无人机正常平稳飞行状态下,为了避免旋转即抵消反力拒,令对角线上的螺旋桨旋转方向相反,一般为螺旋桨1、3拟时针旋转,螺旋桨2、4顺时针旋转,当四个螺旋桨转速相同时,正好互相抵消。
无人机的偏航运动是围绕z轴进行的,若想向右偏航则令螺旋桨1、3的转速提高,螺旋桨1、4的转速降低,令无人机受到的顺时针方向反力拒大于逆时针反力拒;反之向右偏航同理。两方向反力拒的差会使无人机绕z轴旋转,从而实现偏航运动,此外,为了避免运动过程中xy轴方向的影响,使无人机保持水平飞行,改变每组螺旋桨转速大小时应该令两个螺旋桨改变相同的值以避免产生影响xy轴的力矩。
(4)电机分配。将姿态控制中计算出力和力矩对应计算得到对应4个电机的油门控制量。
2.5环境实景构建
2.5.1环境平台介绍
本系统使用FlightGear软件显示飞行仿真的三维实景情况,该软件功能齐全且开源,支持Windows、Linux等多平台运行,并且在Simulink中包含各种用于传输数据的模块,方便使用。
FlightGear在开源的环境下提供了大量的接口供用户使用,在软件中用户可以更改飞行地图、时间等环境,除了软件自身所提供的部分机场地图外,还可以导入自己建模制作的地图。
软件的GUI界面可通过XML文件进行修改利于后续功能的优化和增加,如针对不同的需求提供相应的选项,也可将飞行过程中的各类信息实时显示。
2.5.2 Simulink与FlightGear联合仿真
基于建立好的数学模型,无人机的速度、位置、姿态等状态量会实时动态的受手柄操作而更新,通过将Simulink中完成的建
模运行实时的数据进行处理封装,转换成FlightGear所能接收的数据然后再发送给FlightGear,在FlightGear端设置将数据作为参数传递生成三维图像显示出来。整个过程为单向的数据传输过程,FlightGear端只根据收到的数据更新图像的显示。
(1)FlightGear的接收设置。FlightGear自身支持网络通信,对数据的接收也支持多种协议,在已有动力学模型的情况下设置使用native_fdm协议传输参数。通过软件自身的设置即可在软件端接收UDP方式的native_fdm协议数据。
(2)Simulink的数据封装。该部分由网络通信设置、封装接口设置、对应数据处理三部分构成。首先通过Simulink中的Generate Run Script 模块进行运行路径、网
络通信的设置。脚本设置完毕后开始对数据的处理,在Simulink中提供有Pack net_fdm Packet for Flightgear 模块用于将发送给 Flightgear的数据封装的模块,该模块设置中可以选择Flightgear 版本以及预设的信息类如海拔位置、姿态、发动机状态等,在设置完成后模块会提供相应的数据接口。本系统选择发送的是地面坐标系位置、姿态信息、升降舵、电机转速数量信息。数据处理如图5所示。
数据封装好后,通过Simulink提供的Send net_fdm Packet to FlightGear模块设置好IP、端口信息和输出频率,将封装好的数据以UDP协议发送。
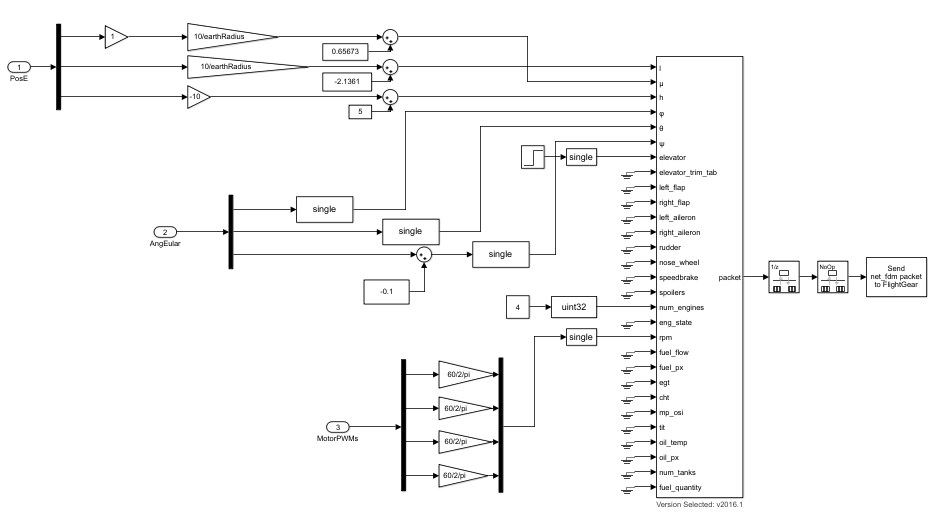
图5 视景仿真系统simulink工程
3 仿真实验与分析
3.1 飞行姿态仿真
接入手柄运行建立的Simulink工程,如图1所示无人机运动画面出现在FlightGear中,使用手柄进行操作,测试俯仰、横滚、
偏航各类型运动效果。如图6所示均运行良好,联合仿真效果达到预期。

图6 姿态效果图
3.2 飞行过程仿真
飞行仿真计算按照图7所示的过程进行,f段进行爬升,g段进行前行,h段进行爬升,j段进行盘旋,k段进行下滑,i段进行前行。
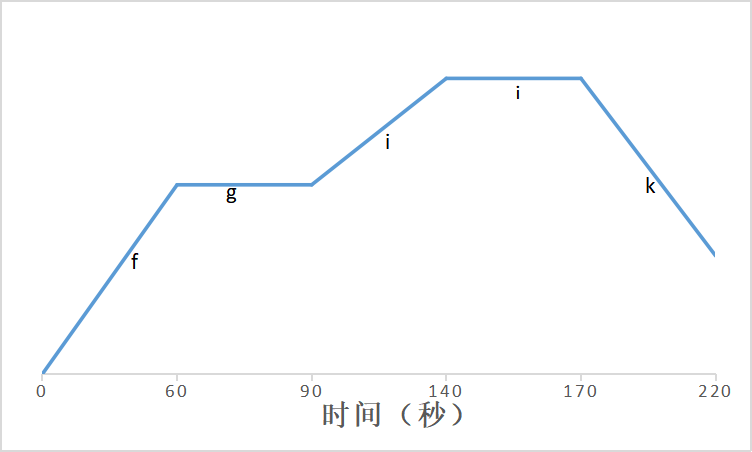
图7 飞行过程
按任务操控遥控器完成飞行任务,利用Simulink提供的功能生成运行过程无人机飞行姿态信息如图8所示。
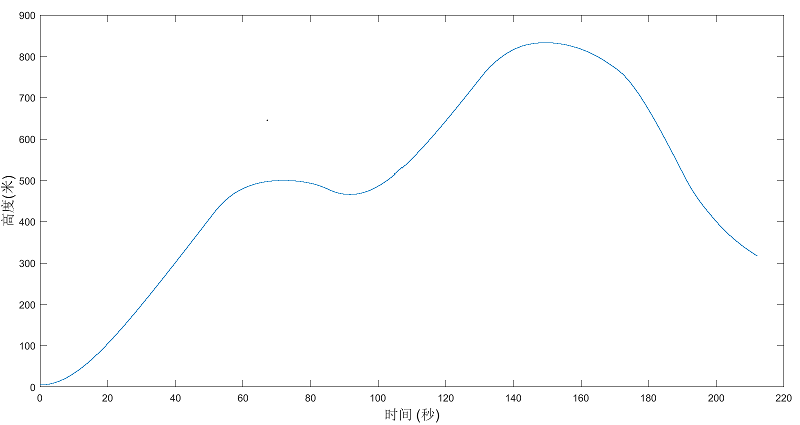
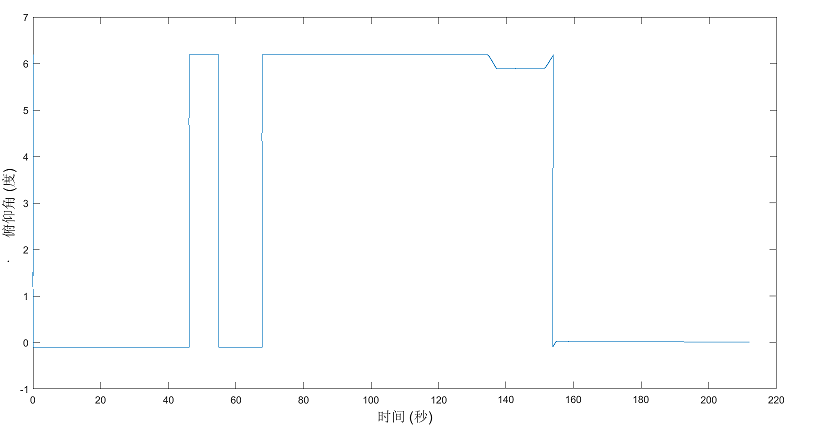
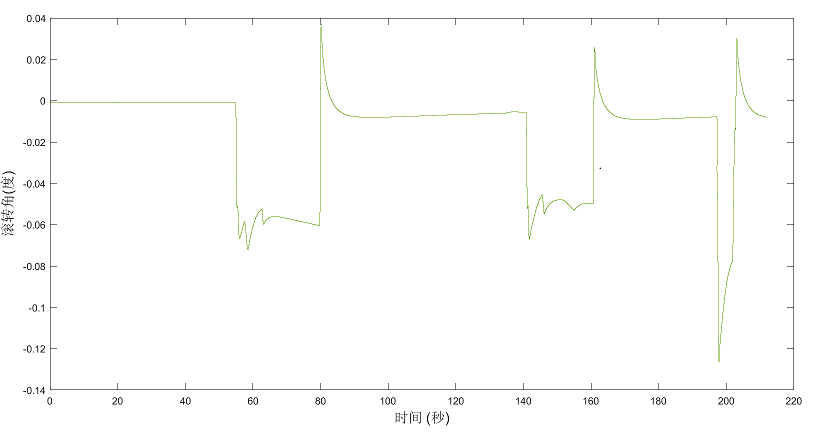
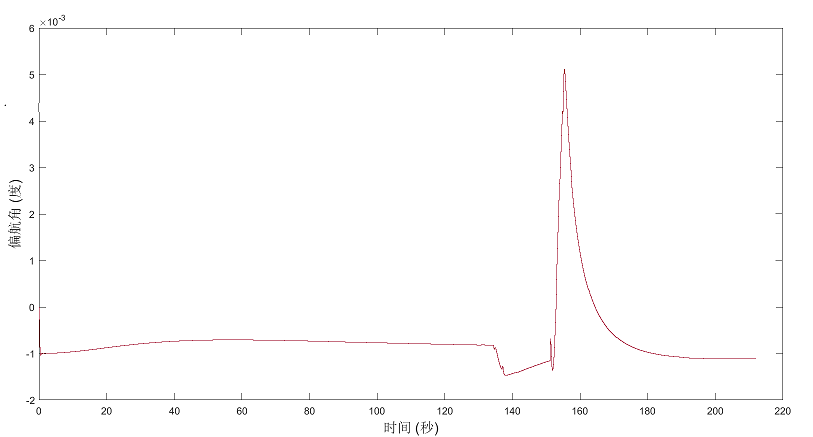
图8 飞行姿态信息
(1)时间0~60秒即f段过程中俯仰角与滚转角为定值没有变化,偏航角受风速影响出现微小波动,因上升过程中油门值固定,上升速度为定值,反应在高度图上近似为斜率固定直线,符合预期。
(2)60~90秒即g段俯仰角有一点延迟,变大向前运动,高度值基本稳定。
(3)90~140秒即h段俯仰角继续增大向前运动,高度增大。
(4)140~170秒即i段盘旋先向左偏航前进10秒后向右偏航完成盘旋运动,向右的偏航角大于向左的偏航角,最后摆正无人机。
(5)170~210秒即j段下降过程,高度恒速下降,机身没有俯仰角变化。
综上飞行过程仿真基本符合预期。
4结束语
本文主要介绍了无人机飞行控制仿真训练系统的整体设计方案,重点阐述了系统构建的三个模块的作用及其联系,能够真实的模拟出无人机的飞行控制。此仿真系统能够很好地展现模拟飞行中无人机姿态信息等相关数据,并以曲线图的方式进行记录。同时系统使用方便、易于维护,可进行更多飞行训练方面的拓展,这对提高训练员的飞行水平 ,节省飞行训练的成本有着极其重要的意义。
参考文献
冯密荣等.世界无人机大全 [M].北京:航空工业出版社,2004.
黄瑞松,李海凤,刘金,孔文华.无人机半实物仿真技术现状与发展趋势分析[J].系统仿真学报,2019,31(09):1763-1774.
矫永康,陈勇,于进勇.无人机模拟训练系统设计与开发[J].计算机测量与控制,2018,26(01):209-212.
王琳,刘元锋,董娇娇,朱秀云.航空摄影测量技术在规划设计教学中的实践和应用[J].福建建筑,2017(03):115-120.
Quan Q, Dai X, Wang S. Multicopter Design and Control Practice [M]. Springer. 2020
基金项目:中国民航大学大学生创新创业项目(202010059055)