关于溶出曲线相似性的两种评价方法分析

关于溶出曲线相似性的两种评价方法分析

池婉君

金华康恩贝生物制药有限公司 浙江省金华市 321000

摘要：在药物固体制剂制备中，体外溶出度试验发挥着举足轻重的作用，而测定溶出趋向已成为对固体制剂品质进行评价重要手段与方法。本文结合当前实况，围绕溶出曲线相似性，探讨了两种评价方法（相似因子法与Weibull分布模型法），望能为此领域研究剖析提供些许借鉴。

关键词：溶出曲线；溶出度；相似性；评价

所谓溶出度，从基础层面来分析，即为药物在在规定条件下从固体制剂（颗粒剂、片剂等）溶出的程度与速度。需要指出的是，尽管单点取样对溶出度进行测定的方法，能够较好的满足常规检验需要，但样品不同，溶出行为存在着较大差异，在此过程中可能会被掩盖，因而经深层比对发现，测定溶出趋向能够将制剂的内在质量更准确且全面的反映出来，是对多因素（采用不同处方工艺等）所造成药物固体制剂质量优劣情况准确区分的重要手段。现阶段，已出现许多评价溶出曲线相似性的方法，其中，比较常用且操作简单的是以列表或者曲线图的形式把溶出数据呈现出来，借此对各种制剂在各时间点的变化关系进行描述，此方法直观且简单。但如果需要同时对读哟中制剂进行比较，此时，此方法的曲线图或列表便会变得复杂或凌乱，且难以提供综合指标，难以做到数据分析的深层化。为此，本文就相似因子法（非模型依赖法）、Weibull分布模型法（模型依赖法）剖析如下。

1.相似因子法

1.1数学表达

在溶出度的各种评价方法当中，相似因子法属于非模型依赖法范畴，主要因为 方程能够提供比较简单的计算方法，相似因子 所对应的数学表达式是：

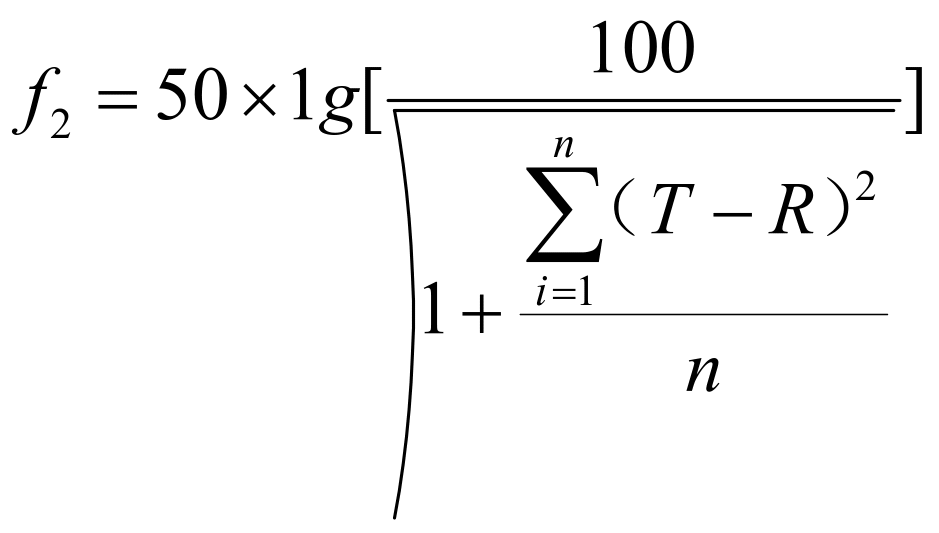
在此公式当中，Ti所表示的是i时间参比制积累释药的占比；Ri代表的则为i时间受试制剂累积释药占比；n所表示的为取样时间点的个数。针对此计算方法而言，其基本假设为参比制剂的累积溶出度与受试制剂差的平方和最小。

在该公式中发现，如果二者有着相同的溶出量（也就是两条溶出曲线重合），对数转化后所得到的 值是100；如果二者在具体的溶出量差值的平方和无穷大，此时， 的值与负无穷大接近，所以，无论是哪一时间点，溶出度差值均不会大于100%， 最小值与0接近时， 的取值区间为0~100，有研究指出，如果 取值范围在50~100之间，提示两制剂有着相同或相近的溶出度。反推，如果有着相似的溶出度曲线，经直观评估，不同时间点累积溶出量差异需＜10%。

1.2应用原则

针对相似因子法而言，其在具体的应用原则上，需要满足如下条件：（1）进行曲线比较的条件。如果是普通制剂，若在15分钟内，其溶出量＞85%，那么不需要开展曲线对比，此时，仿制制剂同样可以满足该要求，如果15分钟时的溶出量没有超过85%，便需开展溶出曲线的比较。（2）明确计算时间点（n）。一般情况下，比较时间点的个数需要≥3个，如果溶出量＞85%，此时的时间点仅能为1个。（3）所选时间点溶出结果变异系数的相关规定。针对参比制剂而言，第一取样时间点所对应的变异系数需＜20%，而自第二取样时间点到最后第一个时间点之间的变异系数需≤10%。（4）测量数量，规定各品种的测定需要取样本12个。（5）含量要求。针对仿制制剂，其在具体含量上，与参比制剂之间的差值需＜5%，且所选样品需要在规定（重量/装量差异）范围内，即＜1/2，尽量将个体差异对溶出度试验数据所造成的影响降至最低。

2. Weibull分布模型法

针对药物释放的不同曲线，同样可采用方程来实施拟合，将与此曲线相符的方程求出来，无论选用哪一种数学方程，其目的均为尽可能使实验数据在所选的函数曲线上。常用模型主要有Weibull分布函数、Higuchi方程及零、一级释放等，释放模型不同，通常采用线性变换之后，通过直线回归得到相关参数，用拟合优度（R₂）、相关系数（r）实施优选。在此些模型当中，最常用的是Weibull分布模型：

t≥α≥0

经推导得知： ，需指出的是，如果将其左边当作Y，ln（t-α）当作X，lnβ当作b，而m当作α，则可将方程列为Y=αX+b，即标准的直线方程。

其中，α、β、m乃是此模型当中的参数，a是位置参数（滞后时间），如果其值为0，此时，提示药物制剂溶出没有时间延滞，如果大于0，提示溶出存在时间延滞；β即尺度参数（就是时间的尺度），如果α、m均维持不变，β取各种值，那么曲线有相同零点，形状相似；m就是形状参数，其对所拟合曲线的形状有决定作用。Y（t）是t时间内药物累积溶出量。

需要指出的是，此模型的常用拟合方法较多，具体见表1。

表1 拟合方法的基本原理及特点

3.结语

综上，本文通过对溶出度曲线相似性比较常用的相似因子法与Weibull分布模型法进行对比、评价。在现实当中，药物溶出实为一个比较繁琐的过程，如果单纯采用一种模型或方法，较难准确得到全部的溶出数据，也就难以实施理想的拟合或对比，因此，药学工作人员需要依据各种方法的基本原理，与现实情况及需要相结合，综合选用，提高溶出曲线相似性评价的准确性与高效性。

参考文献：

[1]邓祖磊, 洪秋菊, 崔田,等. 基于相似系统理论的溶出曲线相似性评价方法[J]. 中国医药工业杂志, 2020, 51(03):98-100.

[2]程莹莹, 陈振阳, 曾环想,等. 硫酸氢氯吡格雷片体外溶出曲线相似性评价[J]. 中国新药杂志, 2018, 027(004):471-476.

[3]张海龙, 严全鸿, 朱海健,等. 多变量置信区间法和模型依赖法在溶出曲线相似性比较中的应用[J]. 药学进展, 2016(12):40-47.

作者简介：池婉君（1990-12-02），女，汉族，籍贯：浙江省金华市，当前职务：QC检验员，当前职称：阻力工程师，学历：本科，研究方向：检验分析方法