基于Anusplin青海省温度空间插值方法研究

基于 Anusplin青海省温度空间插值方法研究

赵敏 达鹏奎

青海省玉树州气象局 815000

摘要：选取地形复杂区域青海省为研究区域，利用2016年50个国家站点气温，将高程作为独立协变量，采用Anusplin对其进行空间插值研究，并挑选出4个站点对其进行精度验证，气温预测对农林也有较好的支撑力，农林业的发展可以改善气候变暖带来的一切问题，提高对农林业的研究支撑，也是对全球变暖的长远策略。验证结果表明96.2%的误差在2.0℃以内的（含2.0℃），3.8%的误差在2.0℃以上，最冷月1月最低气温预测值误差较大，最热月7月平均气温误差均小于等于0.5℃，精度较好。

关键词：青海 空间插值 最高气温 最低气温 平均气温 Anusplin

1 引言

青海省地处青藏高原东北部，地形复杂，地貌多样。全省平均海拔3000多米，与其他省份相比，气象站点分布密度较稀疏，且多分布于谷底和相对平坦的区域^[1]。王思维^[1]、李新^[2]等人用Cokriging多变量估值方法、DW反向距离权重法、Okriging普通克吕格法插值方法、最近邻法^[6][7]对青藏高原气温分布空间插值以及青海地区气温插值进行了对比分析，青藏高原地区的气温空间插值无法采用简单的几何方法或传统统计方法解决的，且由于青藏高原站点分布较稀疏，样本不足，导致以上几种插值方法效果均不理想。而谭剑波^[3]、刘志红^[4]以及钱永兰^[5]等人在研究Anusplin与Cokriging多变量估值方法、DW反向距离权重法等插值方法研究中，对青藏高原东南缘典型山区以及地形复杂的黄土高原中部多沙粗沙区进行插值方法对比得出Anusplin兼顾了曲面平滑度与精确度，具有较强综合能力的空间插值软件，在插值结果中精确度最高，有较好的平滑度，体现出明显优势。

本文引用王思维^[1]、李新^[2] 、谭剑波^[3]等人对Anusplin空间插值方法的研究，基于Anusplin对青海省2016年50个站点气温进行插值研究，将高程作为独立协变量（青藏高原气温空间分布的主要因素是海拔高度的变化）实现研究区气温空间插值研究并进行精度验证，以期对气象、农林业提供参考。

2 、研究区概况

青海省位于中国西北内陆，因境内有全国最大的内陆咸水湖—青海湖而得名。与甘肃、四川、西藏、新疆接壤。青海东部素有“天河锁钥”、“海藏咽喉”、“金城屏障”、“西域之冲”和“玉塞咽喉”等称谓。地势总体呈西高东低，南北高中部低的态势，西部海拔高峻，向东倾斜，呈梯型下降，最高点6860m。最低点1600m。有五分之四以上的地区为高原，东部多山，西部为高原和盆地，兼具青藏高原、内陆干旱盆地和黄土高原三种地形地貌，属高原大陆性气候，地跨黄河、长江、澜沧江、黑河、大通河5大水系。

青海的农业作物以小麦、青稞、蚕豆、马铃薯（土豆）、油菜为主，有高等被子植物近1.2万种，蕨类植物800余种，其中，经济植物75类331属1000余种，涉及药用、纤维、淀粉、糖类、油料、化工原料、香油蜜源、野果野菜、观赏花卉等植物种类。药用植物约500余种，其中，著名中药50多种，主要有冬虫夏草、大黄、贝母、枸杞、甘草、雪莲、藏茵陈、党参、黄芪、羌活、莨菪、麻黄等。日月山以西为牧业区，属高原牧区，牧区内草原广袤，牧草丰美，是我国著名的四大牧区之一。

3、Anusplin空间插值原理

3.1 Anusplin插值简介

本文采用Anusplin空间插值方法，Anusplin是由澳大利亚科学家HUTCHINSON 开发，该方法通过薄盘平滑样条函数进行插值，协变量的引入，根据一组已知的离散数据或分区的数据 , 按照某种关系推求出其他未知点或未知区域数据的数学过程^[3]。目前使用Anusplin软件进行气候类数据插值应用较多，（通常是高程，气象要素的分布一般与高程相关）能够使得插值精度更高，插值结果更为平滑。尤其对气象要素地带性分布特征具有非常好的描述能力，中国气象局制作的全国长时间序列0.5 °气象要素空间分布图就是采用Anusplin软件经站点采样插值而得。

Anusplin包含两个基本模块：Splina和Splinb，功能基本一致，主要区别在于拟合曲面点数的适用性，Splina拟合曲面一般不超过2000个，而Splinb拟合曲面用于10000个，因此在进行气候要素方面数据插值批量处理较为方便，且精度可靠^[5]。

3.2 Anusplin插值方法

Anusplin软件包是使用薄盘平滑样条方法对多变量数据进行内插的工具，包含SPLINA和SPLINB两个基本模块，是Fortran90程序，是利用局部薄盘样条函数根据已知点得到拟合表面。

局部薄盘光滑样条法是对薄盘光滑样条原型的扩展，除普通的样条自变量外允许引入线性协变量子模型，如温度和海拔之间以及降水和海岸线的相关关系。

薄盘光滑样条的理论模型公式如下：

Z_i=f(x_i)+b^ty_i+e_i （i=1,...，N） (1)

式中z_i是位于空间i点的待插值数据，即插值点的气象要素值；x_i为d维样条独立变量矢量，是未知i处周围已知控制点的气象要素值，f是要关于x_i的未知光滑函数；y_i为独立协变量，高程是本次研究的独立协变量；b为独立协变量的系数，e_i为随机误差。

函数f和系数b，利用控制点来求得，将Z_i设置在控制点上，根据其他已知控制点插值该点，通过最小二乘估计来确定，公式如下：

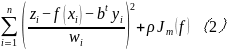
式中：Zi是位于空间i处的控制点的观测值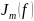； 是函数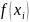 的粗糙度测度函数，是函数 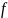的m阶偏导（在Anusplin中称为样条次数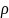）， 是正的光滑参数，是平衡数据的精度和曲面的平滑度。当 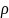接近于零时，曲面经过所有气象数据站点，拟合函数有很好的保真度，当 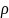无穷大时，函数 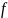接近最小二乘多项式^[3][4]。

4.Anusplin数据处理

本文所用数据来源于全国综合气象信息共享平台的2016年青海省50个国家站点逐月气温数据（最高、最低、平均）气温数据在实际中广泛应用，数据较完整。

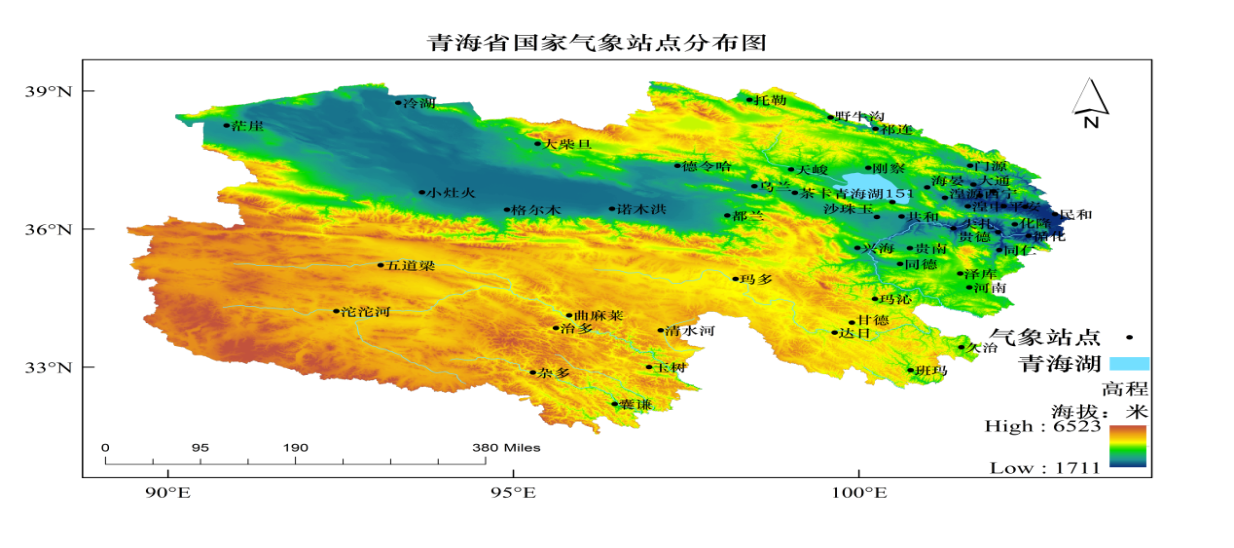
图1青海省50个国家气象观测站分布

将青海省地区TIF格式图像利用Arcgis转换为DEM.txt数据文件。选取青海省2016年冬季1月和夏季7月的最高气温、最低气温以及平均气温，选出4个代表性样点：湟中（52869）、都兰（52836）、五道梁（52908）、甘德（56045）不参与空间插值拟合曲面。原始数据将以剩余46个样点站名、经度、纬度、高程（独立协变量）以及最高气温、最低气温、平均气温观测原值，利用SPSS(Statistical Product and Service Solutions）“统计产品与服务解决方案”软件重组数据将数据另存为固定的ASCII格式.dat 气象变量固定的文件，由于Anusplin需要的是以m为单位的经纬度，故需要在ArcGIS进行ALBERS投影转换得到m为单位的经纬度。如果文件格式不符合，数据存在错误和重复等，在程序执行的过程中会产生错误的提示并中断程序。

将所生成的DEM数据文件以及用SPSS统计分析软件转换生成的数据文件存放至同一文件夹下，包括Anusplin两个基本模块Splina和Splinb拷入数据目录下，开始编写所需的cmd脚本。脚本编写完成后，运行cmd，利用变量局部薄盘光滑样条方法对青海省2016年46个样点1月及7月最高气温、最低气温、平均气温进行拟合曲面空间插值预测代表性4个站点的气温估计值（Lapgrd运行结果grd文件）。

拟合过程中，LOG文件的SIGNAL值处查看Anusplin的最佳模型判断标准，GCV或GML最小，SIGNAL值一般不超过控制点个数的一半且无“*”标出，如出现上述情况，则表明样点数据偏少或数据错误^[3-5]。

将4个样点经度、纬度以及协变量的（通常是高程）加载至Arcgis中，根据经度、纬度以及高程生成空间样本点数据，形成shp格式文件。

将Anusplin插值结果加载至Arcgis中（a-f）依次把4个站点shp格式的经度、纬度以及高程导入至插值表面，并运用空间分析工具中的提取值到点工具，导出各验证样点预测气温数据。

5.Anusplin样条插值精度验证

（a） (b)

(c) (d)

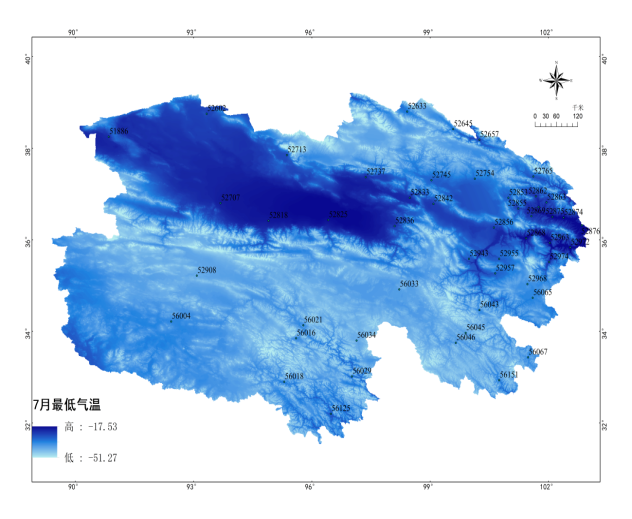
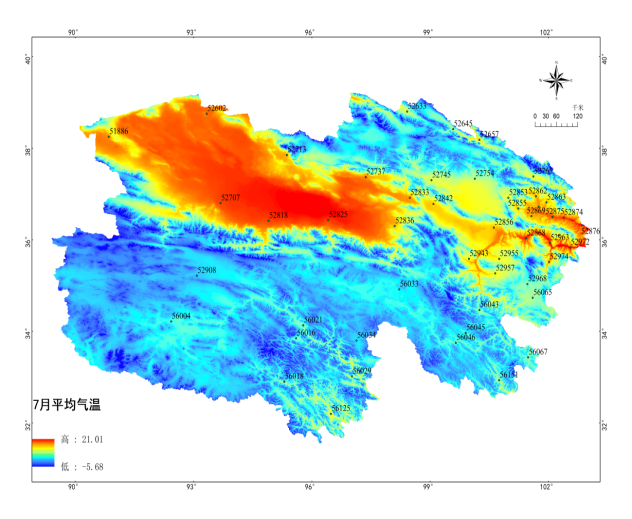(e) (f)

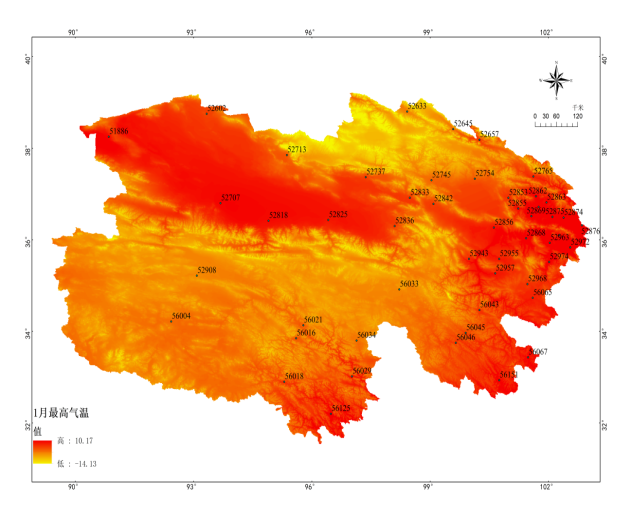
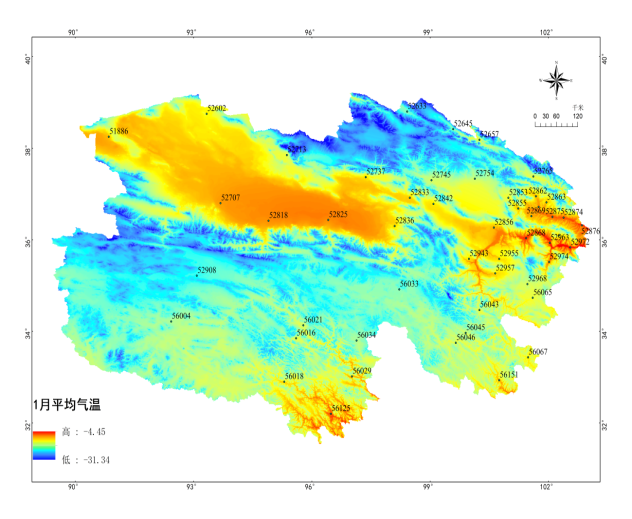
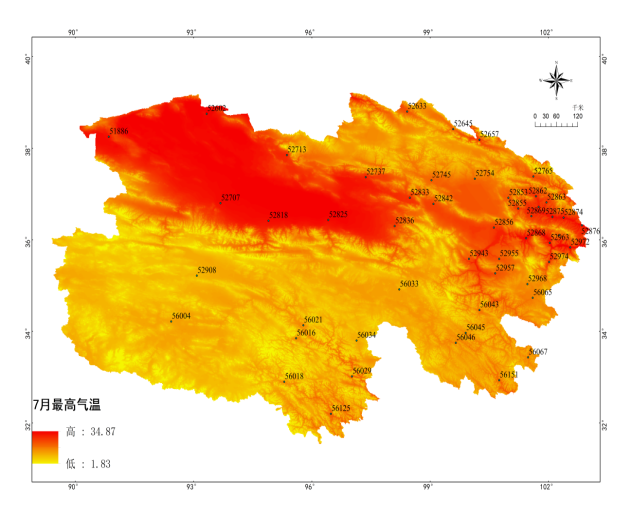
图2 基于Anusplin青海省1月46个样点最高、最低、平均气温插值表面（a、b、c）

基于Anusplin青海省7月46个样点最高、最低、平均气温插值表面（d、e、f）

1月最高气温预测误差值

1月最低气温预测误差值

1月平均气温误差统计

7月最高气温误差统计

7月最低气温误差统计

7月平均气温误差统计

96.2%的误差在2.0℃以内的（含2.0℃），3.8%的误差在2.0℃以上，最冷月1月最低气温预测值误差较大，最热月7月平均气温误差均小于等于0.5℃。

6.结论与讨论

Anusplin包含了交叉验证（GCV）和判断节点充分与否的信号自由度（SIGNAL）的误差统计，比起其他类插值方法有很大的改进^[8]，更加的方便、实用

（1）基于青海省2016年50个国家站点数据，利用Anusplin薄盘样条法对气温要素进行空间插值，移除4个样点：湟中（52869）、都兰（52836）、五道梁（52908）、甘德（56045）1月及7月气温要素，将剩余46个样点进行拟合曲面空间插值，预测4个站点的气温估计值进行检验。

（2）4个样点进行空间插值验证精度，96.2%的误差在2.0℃以内的（含2.0℃），3.8%的误差在2.0℃以上，根据误差值分析得出插值的精度与参与拟合的样点数与分布有密切关系，站点密度较大的湟中（52869）、都兰（52836）插值预测气温误差较小，而五道梁（52908）、甘德（56045）插值预测气温误差较大。且海拔低样点气温预测精度越高。

（3）气温预测对农林也有较好的支撑力，农林业的发展可以改善气候变暖带来的一切问题，提高对农林业的研究支撑，也是对全球变暖的长远策略。

讨论：（精度与地势、站点密度分布特征：样点自身的空间分布是决定插值精度的重要因素，高原地区气温空间分布受海拔影响较大，表现出东高西低，南高北低的分布，青藏高原站点数量较稀疏，如将研究区域扩大或增加研究站点数量密度，将会增加插值结果的可靠性。

参考文献

[1]王思维，刘勇，朱超洪，蒋红.青海省逐日地面气温数据不同插值方法的对比.[J]高原气象，2011

[2] 李新，程国栋，卢玲.青藏高原气温分布的空间插值方法比较. [J]高原气象，2003

[3]谭建波，李爱农，雷光斌. 青藏高原东南缘气象要素Anusplin和Cokriging空间插值对比分析[J]高原气象，2016年04期 第875-886页

[4] 刘志红等人.基于ANUSPLIN的时间序列气象要素空间插值[J]
西北农林科技大学学报(自然科学版)，2008年10期

[5] 钱永兰，吕厚荃，张艳红. 基于ANUSPLIN软件的逐日气象要素插值方法应用与评估[J] 西北农林科技大学学报(自然科学版)2008年第10期　

[6] 刘瑞兵，GIS和SURFER软件在城市大气污染空间分析中的应用[D]青岛：青岛大学，2008

[7] 李述训，吴通华，青藏高原地气温度之间的关系[J] 《冰川冻土》2005年 第5期 627-632页　

[8]朱求安，江洪，宋晓东，基于空间插值方法的中国南方酸雨时空分布格局模拟及分析[J] 2009年 第11期

[9]刘志红等人，基于5变量局部薄盘光滑样条函数的政法空间插值[J] 2006年 第12期

作者简介：赵敏（1991.02），女，汉族，四川省，本科，助理工程师，从事气象业务工作。