核心素养指向下的“单元化主题教学”的实践探索----《正弦函数,余弦函数的性质》教学实施案例

核心素养指向下的“单元化主题教学”的实践探索----《正弦函数、余弦函数的性质》教学实施案例

熊进

西宁市第二中学 ，青海 西宁 810001

一、实施背景

现行高中数学课堂大都是基于线性逻辑结构开展的，对于一个单元的知识，教师往往都是按照既定的逻辑关系去实施教学，以此确保后续知识的学习是建立在前面所学知识的基础之上。这种教学思路使得学生的学科视野受到限制、无法整体上把握学科知识体系、也易出现教师在教学目标的定位、教学内容和教学策略的选择上偏离学生认知水平，不利于数学学科核心素养的培养。

“单元化主题教学”是基于某一单元整体性思考，它与传统的教学模式相比，更加强调教学的整体架构，通过系统的教学框架搭建，寻找单元内部及不同单元之间的关联，围绕某一主题展开教学促进学生整体思维的提升,实现教学效果最优化。“单元化主题教学”在提高学生视角广度的同时，促进对单元知识的有效建构，在建构知识体系的过程中，明确数学思想方法，从而奠定数学学科核心素养培育的基础。

本案例基于“正弦函数、余弦函数的性质”课堂教学，解析如何实施单元整体教学，以期为高中数学课堂教学从“双基”到“数学核心素养”的转变提供参考范式。

二、案例描述

在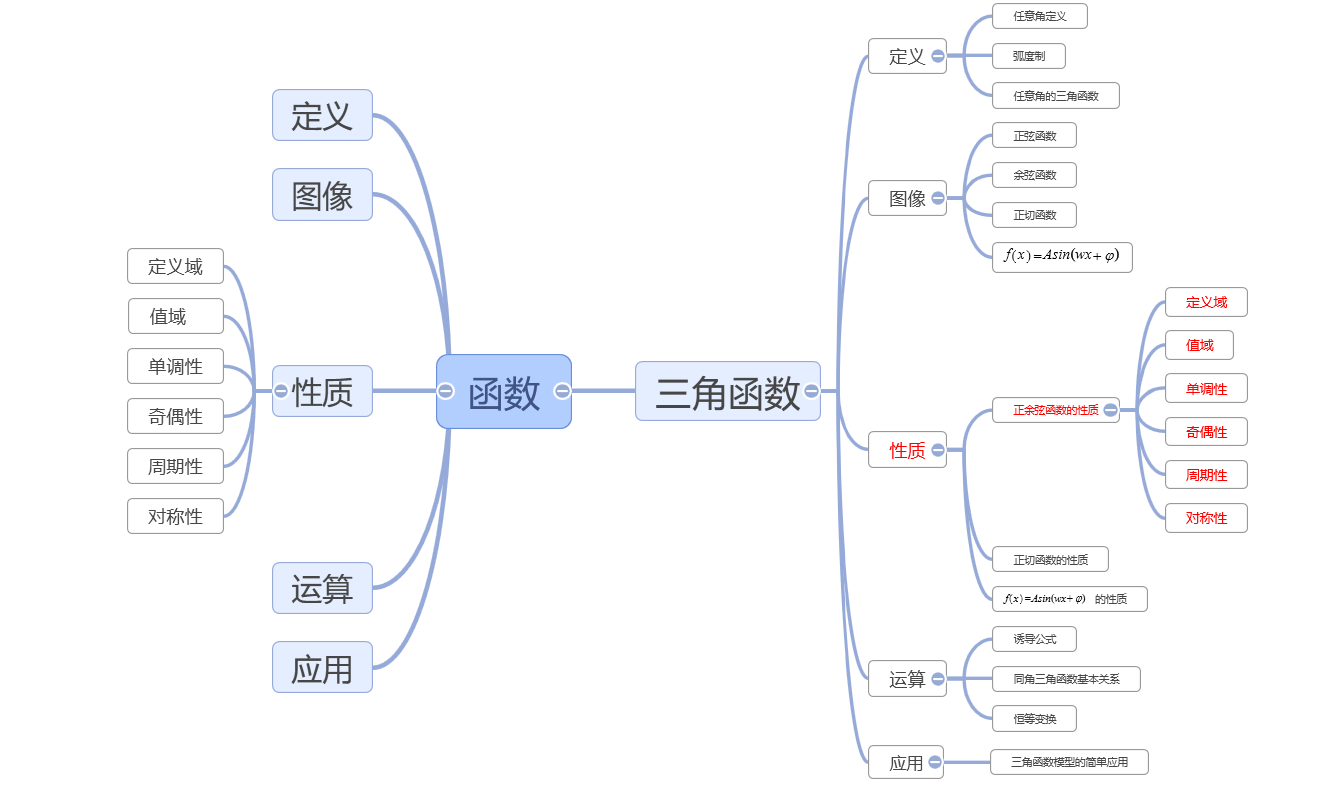
“正弦函数、余弦函数的性质”教学中，授课者立足于必修一函数章节，站在"学生为本"的角度，紧紧围绕“怎样研究一类新函数的性质”来开展教学。依据学生的现有认知特点，从函数单元视角出发，对教材中函数定义、函数图像、函数的性质的探究方法等进行整合、从"大观念"的视野着眼将研究函数的一般性方法内化为学生的一种能力，落实核心素养。

三、案例分析

教学片段1 立足单元结构 问题驱动思考

问题1：我们已经学习了正弦函数、余弦函数的定义，根据以往学习函数的经验，遇到一类新的函数，我们该如何展开研究 ？

设计意图：让学生回顾研究函数问题的一般思路：定义---图像---性质 （值域、单调性、奇偶性、对称性等）。通过这个问题设置，使学生明确了研究的方向。

问题2：该如何研究这些性质呢？ 我们在以往学习中，有没有研究函数性质的成功经历或经验？

设计意图：启发学生回忆具体函数（指数函数、对数函数等） 的研究方法与研究结论，以及一般函数的研究方法和路径，即数形结合的思想，让学生尝试从以往的学习经历中寻找解决新问题的方法，注重把教学活动的重心落在促进学生学会学习上。

问题3：根据正余弦函数 的解析式，你能得出它们的哪些性质？

设计意图：根据解析式理性分析学生能发现它的部分性（如：值域和奇偶性），但“数缺形时少直观”，启发学生进一步探求函数图像，继续寻找函数的其他性质。

问题4：会不会还有其他性质呢？我们想发现正余弦函数的更多性质，仅仅依靠函数解析式看来还不够，需要借助函数的图像，那么如何获取正余弦函数的图像？

设计意图：研究正弦函数的图像是本节课的一个重点，描点法作图是学生已经具有的经验，通过让学生尝试描点法做图，让学生对正弦函数图象有了一个初步的感性认识。

问题5：通过描点法作图我们发现了正弦函数图像的局部轮廓，结合之前学习的诱导公式，同学们能否对正弦函数图像整体轮廓做出一些猜想？

设计意图：让学生作图不是为了作图而作图，而是为以后深刻理解平移三角函数线法作图奠定基础。正弦函数是周期函数这一点可以通过诱导公式加以解释，教师进一步利用几何画板进行展示，让学生观察总结图像特征，从而理解函数图像的变化规律，这样得到正弦函数完整图像便水到渠成。

问题6：如何得到余弦函数图像？正余弦函数从解析式的形式上看，有什么联系？

设计意图：启发学生分别从数和形的角度出发，挖掘解决这一问题的方法。受诱导公式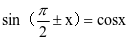 的启发，不难想到可以通过平移正弦曲线得到余弦曲线；另一方面，通过类比正弦曲线做法也可以得到余弦函数的图像，余弦弦函数图像探究路径蕴含着类比的合情推理。

教学片段2 小组合作探究 总结提炼结论

探究1：正弦函数、余弦函数图像有哪些做法？

设计意图：让学生分组讨论并总结出函数图象的作法有描点法 、平移三角函数线法, 教师可再概括为代数作图法和几何作图法 。当学生对正余弦函数图象有了一个感性认识时, 教师再适时地指出 ：决定它们图象的形状有五个关键点，描出这五个点便可作出大致图象,从而将新知识由感性认识真正提高到理性认识。

探究2：由正余弦函数图像你能得到它们哪些性质？

设计意图：学生对图象有了比较透彻的认识后, 教师再引导学生结合图象得到正弦函数的简单性质就较为容易，可要求学生通过类比的方法研究余弦函数的性质。这样的学习不仅可以实现新知的迁移和内化, 而且提高了学生的自主探究能力。

四、案例反思

《正弦函数、余弦函数的性质》的教学从单元整体教学的角度出发，围绕“怎样研究一类新的函数”这条主线引导发现问题、寻找解决问题的办法（类比）、得到解决问题的普遍性方法，整个过程以问题来驱动学生思考，丰富了学生的认知体验、还原学生本位。从知识获取途径、思想方法渗透、活动体验等方面，使学生对函数章节结构有了整体的认知，较好落实了数学核心素养。

参考文献

[1]基于初中视角的初高中数学教学衔接实践研究[J]. 刘勇. 华夏教师. 2019(31)

[2]数学教学歌曲辅助高中数学教学实验研究[J]. 魏豪,徐章韬. 教师教育论坛. 2017(06)

[3]实施“三导”策略 优化数学教学[J]. 王微. 数学大世界(下旬). 2020(12)