基于球齿轮平面3RRR并联机构运动学研究

基于球齿轮平面 3RRR并联机构运动学研究

薛明瑞1

浙江工业职业技术学院 浙江绍兴 312000

摘要：针对并联机构工作空间较小的问题，本文通过将球齿轮齿盘机构与平面3RRR机构相结合，实现将平面移动转换成空间转动，既保持并联机构刚度较大、承载能力强等特点，也扩展了其工作空间。

关键词：球齿轮；3RRR并联机构；运动学

0 引言

并联机器人或并联机构^[1]（PM）可定义为由多个并行链构成的闭环运动系统，即指由末端执行器（动平台）、机架（定平台）以及连接于两者之间的2条或2条以上的独立运动链组成，且以并联方式驱动的闭环机构。并联机器人有着工作空间小、刚度大、灵活性好、承载能力强、精度高、自重负荷小、动力学性能好等优点，被广泛应用于飞行模拟器、微动定位机器人、数控加工中心等。

随着工业水平的不断提高，零件造型越来越复杂，加工精度要求不断提高，对机床实现多轴加工的要求越来越迫切。并联机床可实现多轴联动，对复杂曲面零件进行加工，但其存在工作空间小，外形体积较大的缺点。球齿轮传动具有两个运动自由度, 可将平面运动转换成二维转动。本文采用平面3RRR机构与球齿轮传动机构相结合如图1所示，实现对大型复杂零件的加工。

图1七轴并联机床

1 平面3RRR并联机构运动分析

由图2所示平面3RRR并联机构定平台A₁A₂A₃为边长l₁的正三角形，动平台C₁C₂C₃为边长l₄的正三角形，A₁B₁= A₂B₂= A₃B₃=l₂， B₁ C₁= B₂ C₂= B₃ C₃=l₃，A_iB_i与x轴的夹角为θ_i，动平台x₁轴与x轴的夹角为θ。

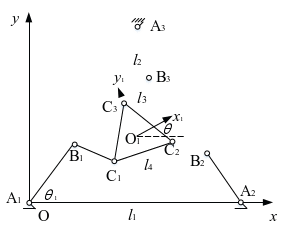
图2平面3RRR并联机构运动简图

根据几何关系^[2,3]可得，B_i坐标与各输入θ_i关系为：

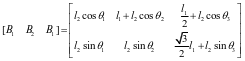
C_i在动坐标系的坐标为：

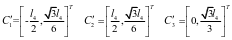
C_i在定坐标系中的坐标与(x,y,θ)之间的关系为：

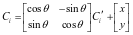
再由约束方程 求出θ_i与(x,y,θ)之间的关系。

2 球齿轮齿盘机构的运动分析

在球齿轮齿盘机构中,若齿盘为主动件时,可将齿盘沿 x-y方向的平动, 转换为球齿轮的二维旋转运动。由文献可得输出轴的末端坐标[x_ey_ez_e]^T与[x y] ^T的关系为：

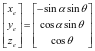
式中： ，

从而可得出[θ₁ θ₂ θ₃] ^T与[x_ey_ez_e]^T的关系。

结论：

通过将球齿轮齿盘机构与平面3RRR机构结合，实现将平面移动转换成空间转动，既保持并联机构刚度好、重载等特点，也扩展了其工作空间。

参考文献：

[1]薛明瑞. 2PRU-(2PRR)U并联机构运动学及性能分析[D].浙江理工大学,2015.

[2]张乾坤,高洪.3-RRR并联机器人运动学建模与仿真[J].巢湖学院学报,2017,19(06):54-59.

[3]李春林,赵小团.平面3自由度并联机构运动分析[J].现代经济信息,2008(12):99-100.

[4]潘存云,温熙森.渐开线环形齿球齿轮传动原理与运动分析[J].机械工程学报,2005(05):1-9.

基金项目：浙江省教育厅一般科研项目(Y201941467)。

作者简介：薛明瑞(1986-)，男，在读博士研究生，主要从事机器人研究

1