湖南省怀化市溆浦县第一中学,湖南省 怀化市 419300
摘要:普通高中新课程标准中指出数学建模是一种重要的数学核心素养。概率统计应用题在高考中一般会出一大题,是考查学生分析、解决数学应用题能力的重要题型。下面例举几题说明高考如何考查概率统计应用题,考查的难度有多大。便于同学们复习备考。
关键字:概率统计; 应用题;建模
1.随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为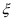 .
.
(1)求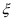 的分布列;(2)求1件产品的平均利润(即
的分布列;(2)求1件产品的平均利润(即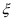 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
【分析】本题考查的是随机变量的分布列及期望的实际运用.对于(1)可先将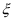 的各种可能值对应的概率求出,然后代入公式可得(2)的答案
的各种可能值对应的概率求出,然后代入公式可得(2)的答案
【详解】(1)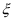 的可能取值有
的可能取值有 ;
;


故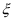 的分布列为
的分布列为
| 6 | 2 | 1 | -2 |
P | 0.63 | 0.25 | 0.1 | 0.02 |
(2)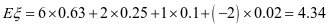
(3)设技术革新后的三等品率为x,则此时1件产品的平均利润
 ,
,
依题意 ,
,
所以三等品率最多是 .
.
2.根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立.
(Ⅰ)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(Ⅱ)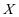 表示该地的100位车主中,甲、乙两种保险都不购买的车主数.求
表示该地的100位车主中,甲、乙两种保险都不购买的车主数.求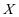 的期望.
的期望.
【详解】(Ⅰ)设该车主购买乙种保险的概率为 ,则
,则 ,故
,故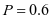 ,
,
该车主甲、乙两种保险都不购买的概率为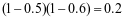 ,
,
由对立事件的概率该车主至少购买甲、乙两种保险中的1种的概率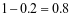
(Ⅱ)甲、乙两种保险都不购买的概率为0.2,
所以
3.设甲、乙两位同学上学期间,每天7:30之前到校的概率均为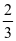 .假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用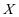 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量
表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量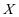 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设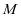 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件
为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件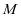 发生的概率.
发生的概率.
【分析】(Ⅰ)由题意可知分布列为二项分布,结合二项分布的公式求得概率可得分布列,然后利用二项分布的期望公式求解数学期望即可;
(Ⅱ)由题意结合独立事件概率公式计算可得满足题意的概率值.
【详解】(Ⅰ)因为甲同学上学期间的三天中到校情况相互独立,且每天7:30之前到校的概率均为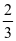 ,故
,故 ,从面
,从面 .
.
所以,随机变量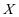 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
| | | | |
随机变量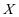 的数学期望
的数学期望 .
.
(Ⅱ)设乙同学上学期间的三天中7:30之前到校的天数为 ,则
,则 .
.
且 .
.
由题意知事件 与
与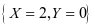 互斥,
互斥,
且事件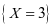 与
与 ,事件
,事件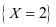 与
与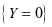 均相互独立,
均相互独立,
从而由(Ⅰ)知: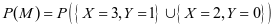


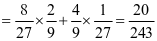 .
.
【点睛】本题主要考查离散型随机变量的分布列与数学期望,互斥事件和相互独立事件的概率计算公式等基础知识.考查运用概率知识解决简单实际问题的能力。
4.甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为 ,(1)求甲连胜四场的概率;(2)求需要进行第五场比赛的概率;(3)求丙最终获胜的概率.
,(1)求甲连胜四场的概率;(2)求需要进行第五场比赛的概率;(3)求丙最终获胜的概率.
【分析】(1)根据独立事件的概率乘法公式可求得事件“甲连胜四场”的概率;
(2)计算出四局以内结束比赛的概率,然后利用对立事件的概率公式可求得所求事件的概率;
(3)列举出甲赢的基本事件,结合独立事件的概率乘法公式计算出甲赢的概率,由对称性可知乙赢的概率和甲赢的概率相等,再利用对立事件的概率可求得丙赢的概率.
【详解】(1)记事件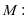 甲连胜四场,则
甲连胜四场,则 ;
;
(2)记事件 为甲输,事件
为甲输,事件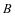 为乙输,事件
为乙输,事件 为丙输,则四局内结束比赛的概率为
为丙输,则四局内结束比赛的概率为
 ,
,
所以,需要进行第五场比赛的概率为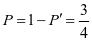 ;
;
(3)记事件 为甲输,事件
为甲输,事件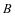 为乙输,事件
为乙输,事件 为丙输,记事件
为丙输,记事件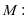 甲赢,记事件
甲赢,记事件 丙赢,
丙赢,
则甲赢的基本事件包括: 、
、 、
、 、
、
 、
、 、
、 、
、 、
、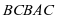 ,
,
所以,甲赢的概率为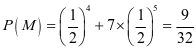 .
.
由对称性可知,乙赢的概率和甲赢的概率相等,所以丙赢的概率为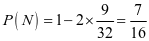 .
.
【点睛】本题考查独立事件概率的计算,解答的关键就是列举出符合条件的基本事件,考查计算能力。
【参考文献】
1.简洪权.高中数学运算能力的组成及培养策略.《中学数学教学参考》
2.张卫国.例谈高考应用题对能力的考查.《中学数学研究》
3.黄立俊、方水清.增强应用意识,增强建模能力.《中学数学通讯》
4.薛治刚.《高中数学应用问题》吉林科学技术出版社
试卷第1页,总4页