初中数学三角函数解题技巧探究

初中数学三角函数解题技巧探究

阿依努尔 ·肉孜

喀什市 第一中学 新疆喀什 844000

摘 要：三角函数是初中数学课程中一项重要内容，也是三角函数部分的基础，对初中数学三角函数解题技巧的掌握是学生必须具备的技能，为学生长期的学习和发展奠定基础。三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。三角函数部分知识点多，需要学生了解和掌握的公式繁琐，导致很多学生基础知识掌握不牢，学习出现问题。本文从初中数学三角函数解题技巧的研究出发，致力于探索出更多的解题方法，挖掘更多更合理的三角函数教学策略，为三角函数部分的学习奠定基础。

关键词：初中数学 三角函数 解题技巧

在整个初中数学的学习阶段，三角函数部分占据着很重要的地位。初中的三角函数具有很多琐碎的知识点，例如，勾股定理、正弦定理、余弦定理等，在解题时需要学生综合运用各部分知识点。三角函数是数学中常见的一类关于角度的函数，也可以说以角度为自变量，角度对应任意两边的比值为因变量的函数叫三角函数，三角函数将直角三角形的内角和它的两个边长度的比比值相关联，也可以等价地用与单位圆有关的各种线段的长度来定义。这就需要学生灵活的掌握知识、掌握解题方法。需要教师认真的探索和研究，总结出更多的解题策略和解题技巧，提高学生对三角函数学习的积极性，让学生在数学中体验到学习的乐趣，热爱学习，进而提高学习效率。

一、合理运用正弦、余弦定理进行边角互化

正余弦定理是正弦定理、余弦定理，是揭示三角形边角关系的重要定理，直接运用它可解决三角形的问题，若对余弦定理加以变形并适当移于其它知识，则使用起来更为方便、灵活。在初中数学三角函数部分，正弦余弦定理是最基本的性质，也是解题时进行边角互化的重要工具和途径。因此，学生必须掌握边角互化的意识和技能，在解题时才会更加简单方便。

二、巧妙利用勾股定理，解决三角函数问题

某数学兴趣小组同学进行测量大树CD高度的综合实践活动，如图，在点A处测得直立于地面的大树顶端C的仰角为36°，然后沿在同一剖面的斜坡AB行走13米至坡顶B处，然后再沿水平方向行走6米至大树脚底点D处，斜面AB的坡度(或坡比比) i=1: 2.4，那么大树CD的高度约为(参考数据sin36°≈0.59， cos36°≈0.81tan36°≈0.73) ( )

A.8.1米 B.17.2米 C.19.7米 D.25.5米

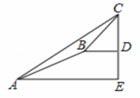【 分析】作BF⊥AE于F，则FE=BD=6米，DE=BF，

设BF=x米，

则AF=2.4米，

在Rt△ABF中，由勾股定理得出方程，

解方程求出DE=BF=5米，AF=12米，得出AE的长度，在Rt△ ACE中，由三角函数求出CE，即可得出结果

解: 作BF⊥AE于F，如图所示:

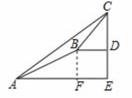
则FE=BD=6米，DE=BF，

因为斜面AB的坡度i=1: 2.4，

所以AF=2.4BF，

设BF=x米，则AF=2.4x米

在Rt△ABF中，由勾股定理得: x²+(2.4x) ²=132，

解得: x=5

DE=BF=5米， AF=12米

AE=AF+FE=18米

在在Rt△ACE中，

CE=AE.tan36=18×0.73=13.14米，

所以CD=CE- DE=13.14米-5米≈8.14米;所以选A

点评：本题考查了解直角三角形的应用、勾股定理、三角函数;由勾股定理得出方程是解决问题的关键。

三、建立数学模型，将复杂的问题简单化

例题：如图，厂房屋顶人字形(等腰三角形)钢架的跨度

BC=10米，∠B=36°，则中柱AD (D为底边中点)的长是 ( )。

A.5sin36° 米 B.5cos36°米

C.5tan36°米 D.10tan36°米

分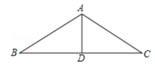 析：根据等腰三角形的性质得到 DC=BD=5米，在Rt△ ABD中，利用∠B的正切进行计算即可得到AD的长度.

[解答]解: . AB=AC，AD⊥BC，

BC=10米，DC=BD=5米，

在Rt△ADC中，∠B=36°，

tan36°= AD/BD 即AD=BDtan36°=5tan36° (米)

故选:C.

点评：本题考查了解直角三角形的应用。解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题。

总之，三角函数部分是初中数学教学的重要组成部分，也是以后三角函数学习的基础。在初中阶段的学习中，由于学生第一次接触这部分知识，难以熟练的掌握三角函数的知识点，解题时也不知道该运用什么样的技巧。本文通过对三角函数解题技巧的探究，旨在为学生提供更多的解题策略，提高三角函数部分的学习质量。希望以上策略能运用到三角函数解题中，激发学生的数学学习兴趣，自主学习，热爱学习，合作探究，提高学习效率。

参考文献：

1. 何秀杰.发现三角函数的基本性质[A].2017年区域优质教育资源的整合研究研讨会成果集，2017.

2. 王曦之.22.5°和15°三角函数值的几何计算方法探究[A].国家教师科研专项基金科研成果(十三)，2017.

3. 唐伟.一道三角函数问题的思考[A].2016年4月现代教育教学探索学术交流会论文集， 2016.

[4]白晓丽 .《锐角三角函数》一章易错点的提前干预[A].2016年9月全国教育科学学术交流论文汇编， 2016.