南京市栖霞中学 210046
摘要:本文主要基于2020全国Ⅰ卷圆锥曲线中一个定点问题的思考,探究在一般的椭圆方程中得出相应的结论1,将结论1再一次推广到更为一般的情形;最后类比到圆中得出相应的结论,培育学生数学运算、直观想想等数学核心素养。体现了对高考题探究的一般思路,提高学生对数学问题的追根溯源的深度学习与探究学习兴趣。
关键词:圆锥曲线 定点问题 逻辑推理 探究学习
圆锥曲线中的定点问题一直是高考的热点问题,近年来全国各地高考卷中对这类问题的考查多有涉及,这类问题往往背后所蕴含的是圆锥曲线的一个一般性的结论,学生在平时备考阶段往往通过题海战术只是了解这类问题的表象。我们在平时教学时应该注重引导学生对问题进行深入探究,积极挖掘定点问题背后所蕴含的一般性结论(如文[1]的探究方法),从而促进学生对数学学习的深度和广度以及培养学生的探索钻研精神,笔者主要借助于2020全国Ⅰ卷中压轴题的定点问题,对其进行探究与类比,得出相应结论,展示探究这类问题的一般思路。
一、试题展示与解答
(2020全国Ⅰ卷,文,21)已知![]() 为椭圆
为椭圆![]()
![]() 的左、右两个顶点,
的左、右两个顶点,![]() 为
为![]() 上顶点,
上顶点,![]() 。
。 ![]() 为直线
为直线![]() 上动点,
上动点,![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,
,![]() 与
与![]() 的另一个交点为
的另一个交点为![]()
求![]() 的方程;
的方程;
证明:直线![]() 过定点。
过定点。
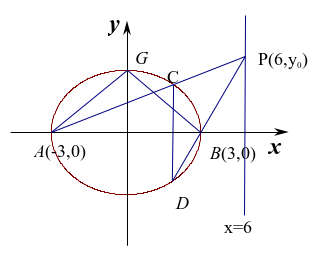
图1
解:(1)![]() 。
。
(2)如图1所示:设![]() ,根据题意:
,根据题意:![]() 、
、![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,与椭圆
,与椭圆![]() 联立
联立![]() ,得:
,得:![]() ,由于直线
,由于直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() ,根据韦达定理可知:
,根据韦达定理可知: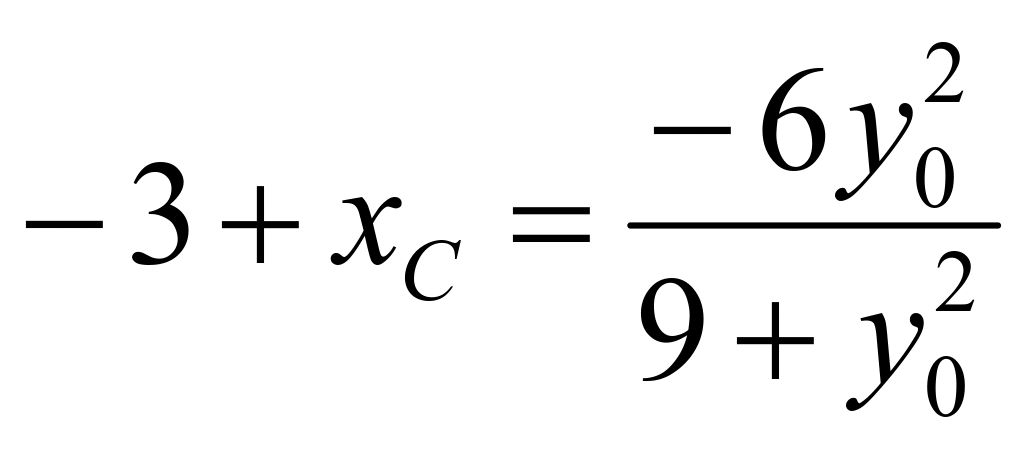 ,所以可知:
,所以可知: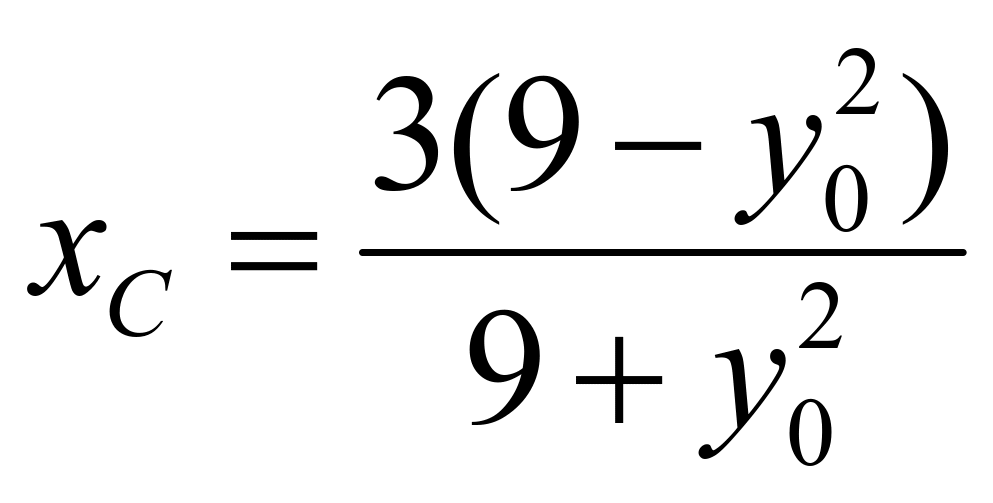 ,代入直线
,代入直线![]() 方程得:
方程得:![]() ,同理:直线
,同理:直线![]() 的方程为:
的方程为:![]() ,与椭圆
,与椭圆![]() 联立
联立![]() ,化简得:
,化简得:![]()
![]() ,由于直线
,由于直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() ,根据韦达定理可知:
,根据韦达定理可知: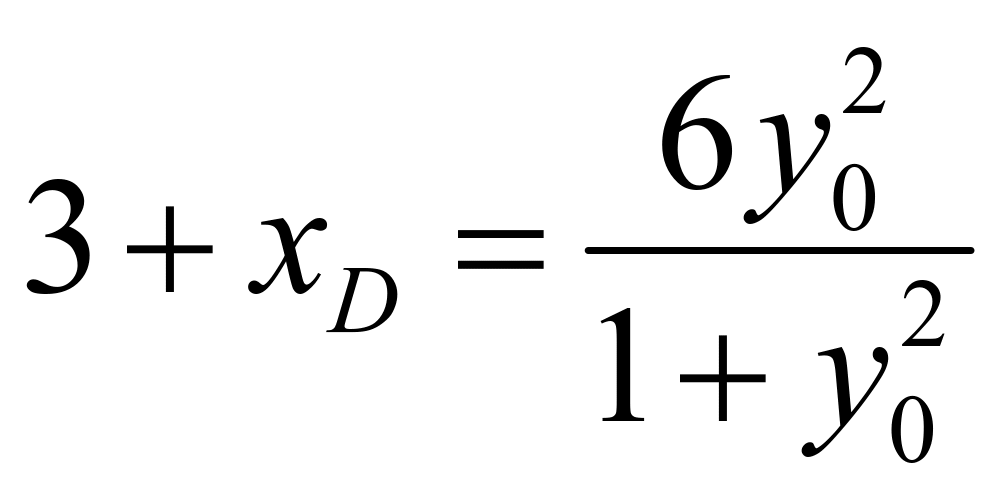 ,所以可知:
,所以可知: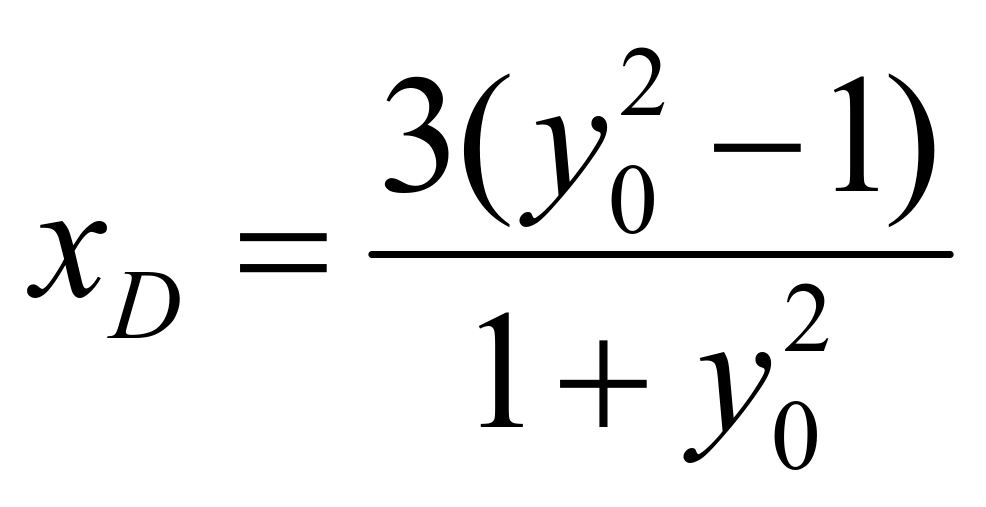 ,则
,则![]() ,当直线
,当直线![]() 斜率存在时,根据两点式可以写出直线
斜率存在时,根据两点式可以写出直线![]() 方程:
方程:![]() ,代入化简得:
,代入化简得:![]() ,所以直线
,所以直线![]() 过点定点
过点定点![]() ;当直线
;当直线![]() 斜率不存在,
斜率不存在,![]()
![]() ,有
,有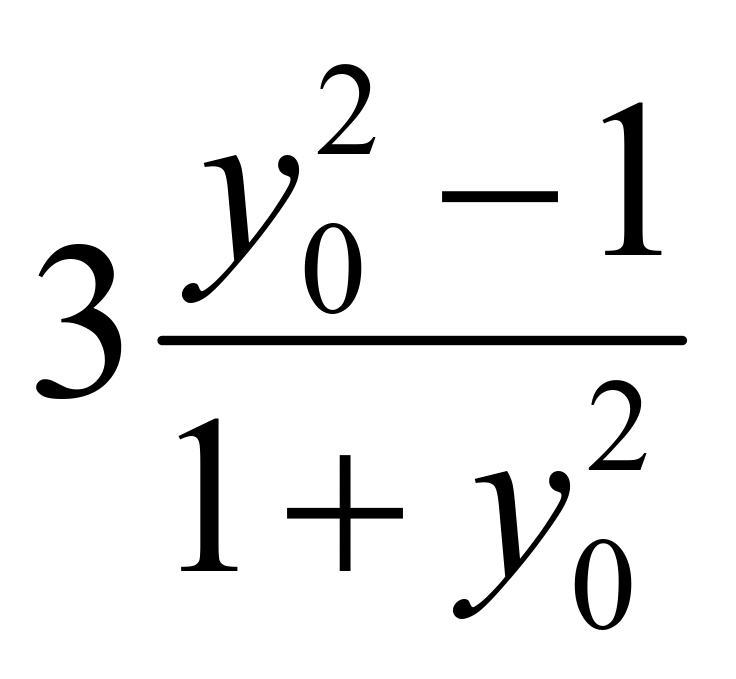
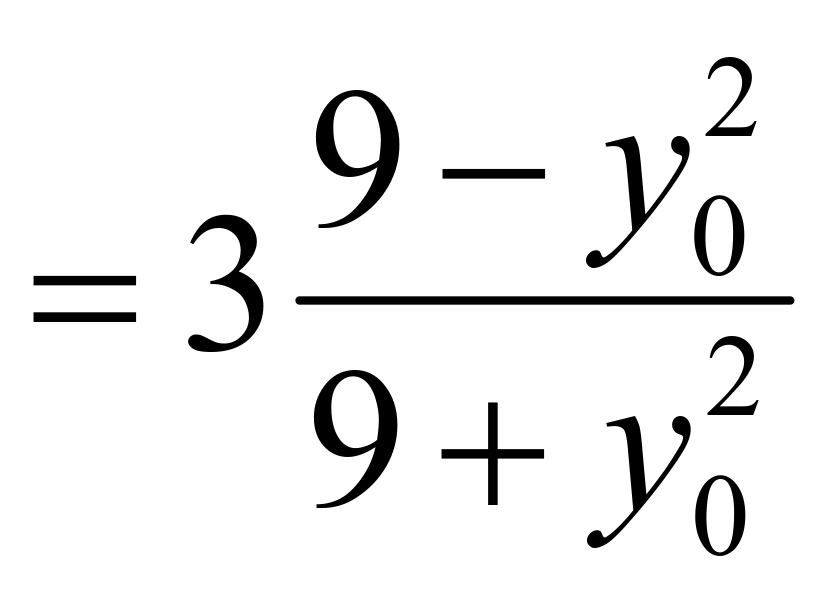 ,化简可知:
,化简可知:![]() ,所以
,所以![]() ,所以直线
,所以直线![]() 也过定点
也过定点![]() 。
。
提炼结论
对上述的结果进行剖析:我们发现![]() 恰好是
恰好是![]() ,而且结论中的定点为
,而且结论中的定点为![]() ,也恰好是
,也恰好是![]() ,猜想:对于一般的椭圆中也有这样的结果。现将其在一般的椭圆方程进行探究,将有如下的结论:
,猜想:对于一般的椭圆中也有这样的结果。现将其在一般的椭圆方程进行探究,将有如下的结论:
结论1:已知![]() 为椭圆
为椭圆![]()
![]() 的左、右两个顶点,
的左、右两个顶点,![]() 为直线
为直线![]() 上动点,
上动点,![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,
,![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,则直线
,则直线![]() 过定点
过定点![]() 。
。
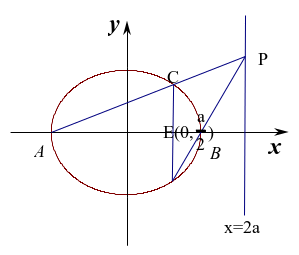
图2
证明:如图2:设![]() ,由题意可知
,由题意可知![]() ,
,![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,与椭圆
,与椭圆![]() 联立
联立![]() ,得:
,得:![]() ,由于直线
,由于直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() ,根据韦达定理可知:
,根据韦达定理可知: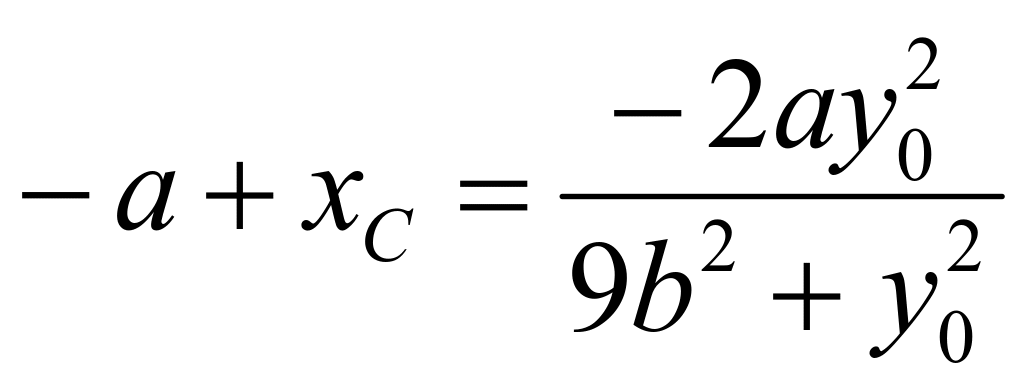 ,所以可知:
,所以可知: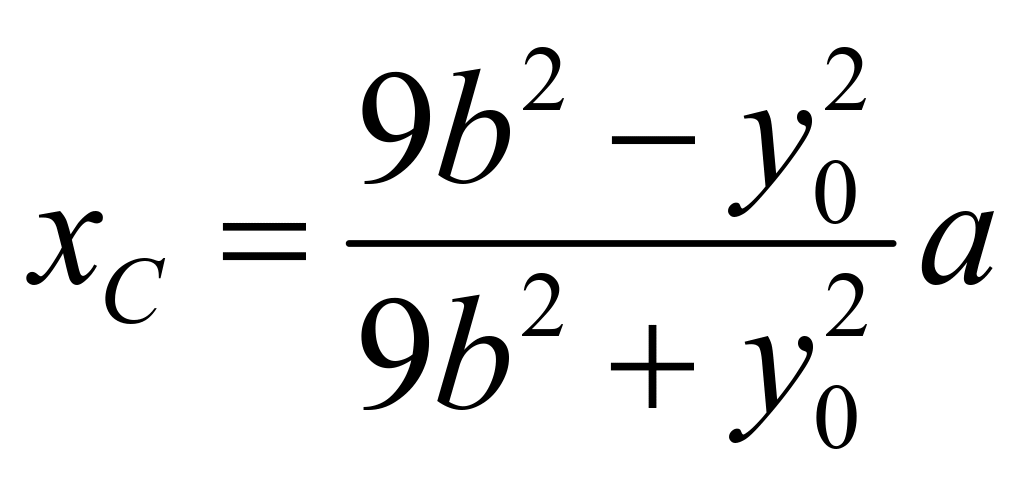 ,代入直线
,代入直线![]() 得
得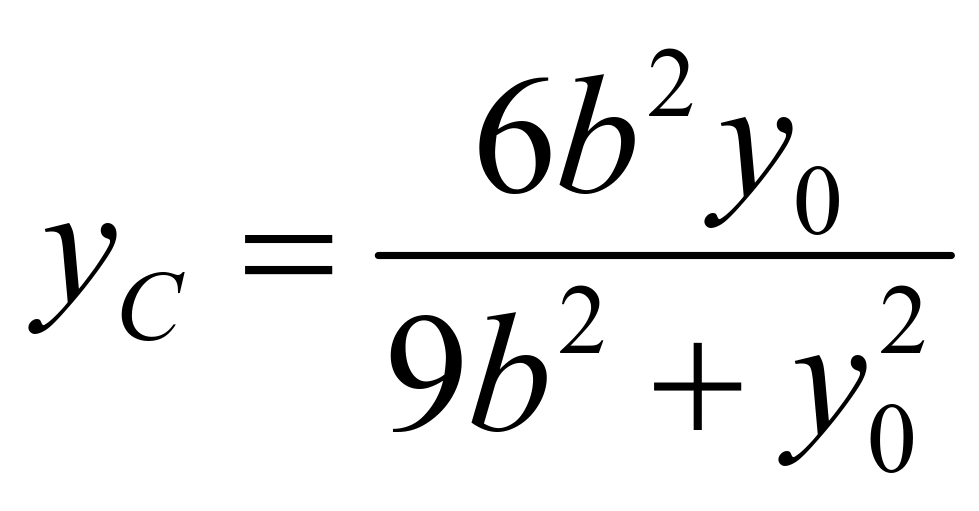 ,同理:直线
,同理:直线![]() 的方程为:
的方程为:![]() ,与椭圆
,与椭圆![]() 联立
联立![]() ,得:
,得:![]()
![]() ,由于线
,由于线
![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() ,由韦达定理可知:
,由韦达定理可知: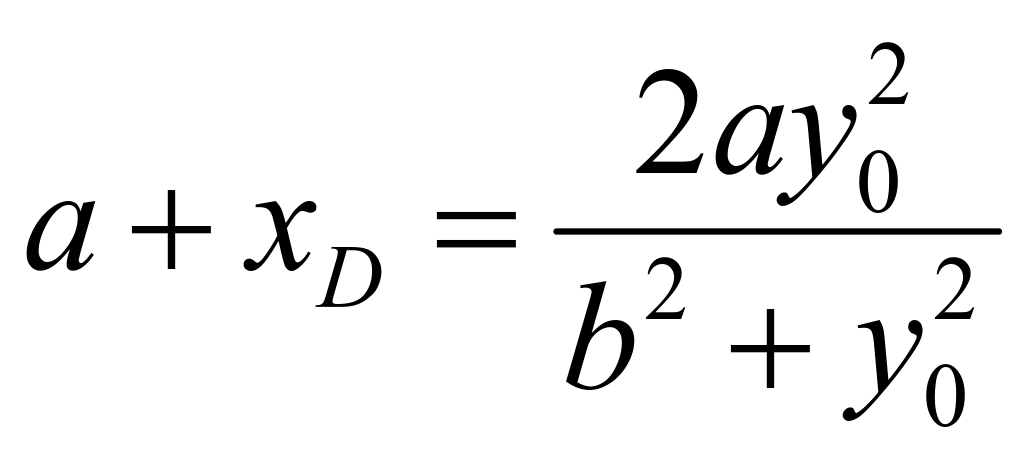 ,所以可知:
,所以可知: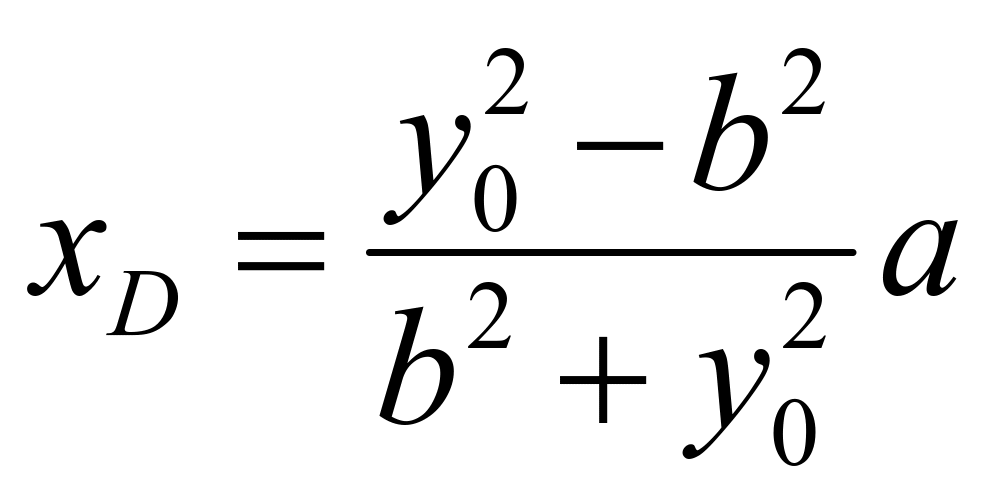 ,代入直线
,代入直线![]() 得:
得: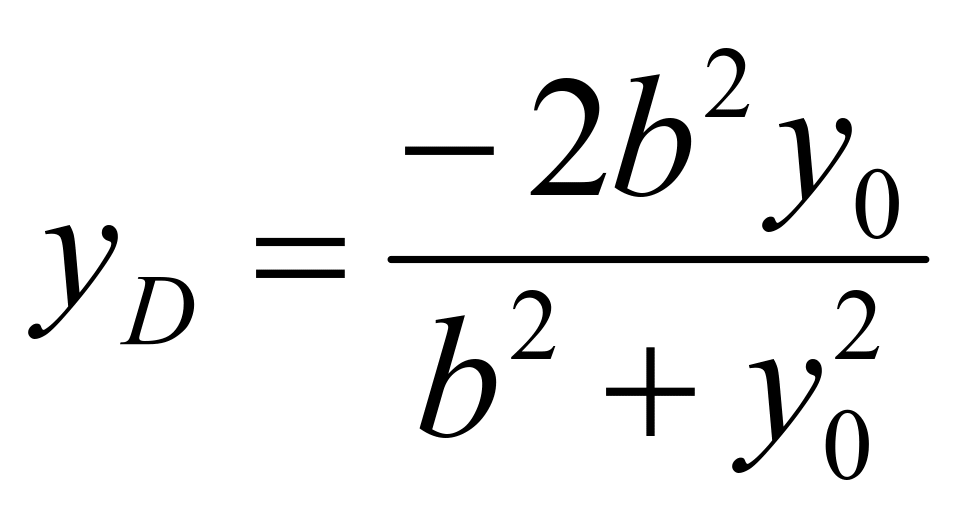 ,当直线
,当直线![]() 斜率存在时,根据两点式写出直线
斜率存在时,根据两点式写出直线![]() 方程:
方程:![]() ,代入化简得:
,代入化简得: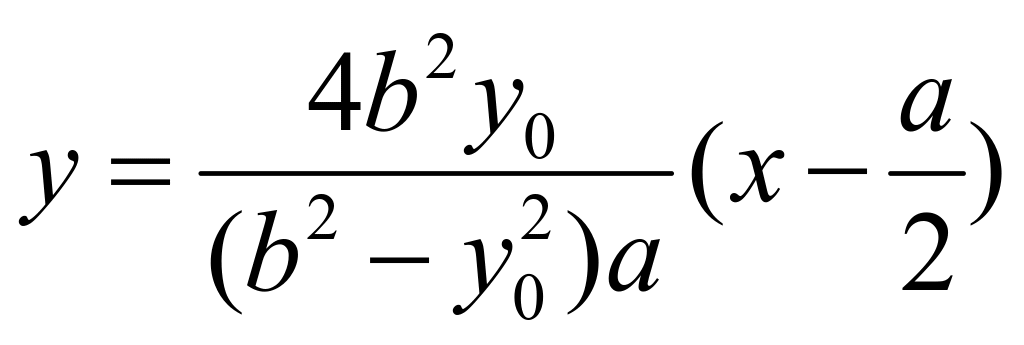 ,所以直线
,所以直线![]() 过点定点
过点定点![]() ;当直线
;当直线![]() 斜率不存在,
斜率不存在,![]()
![]() ,有
,有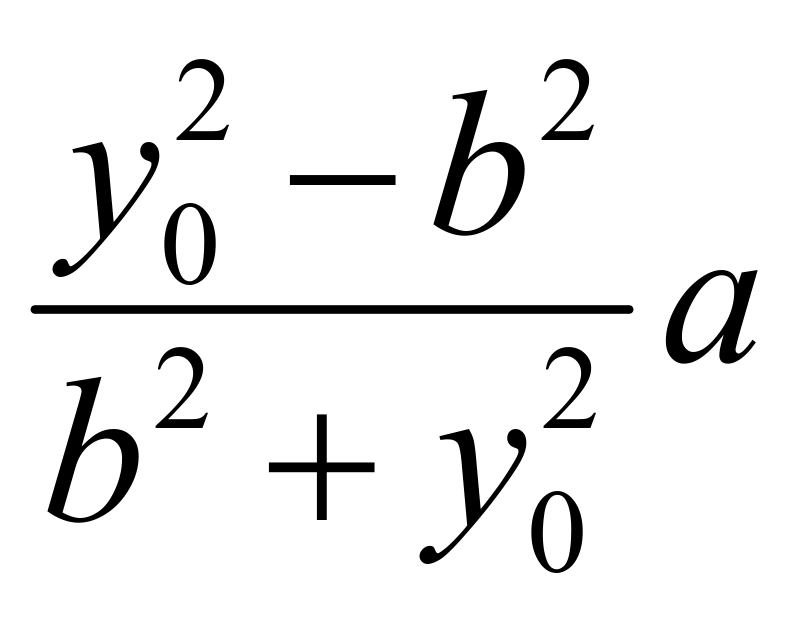
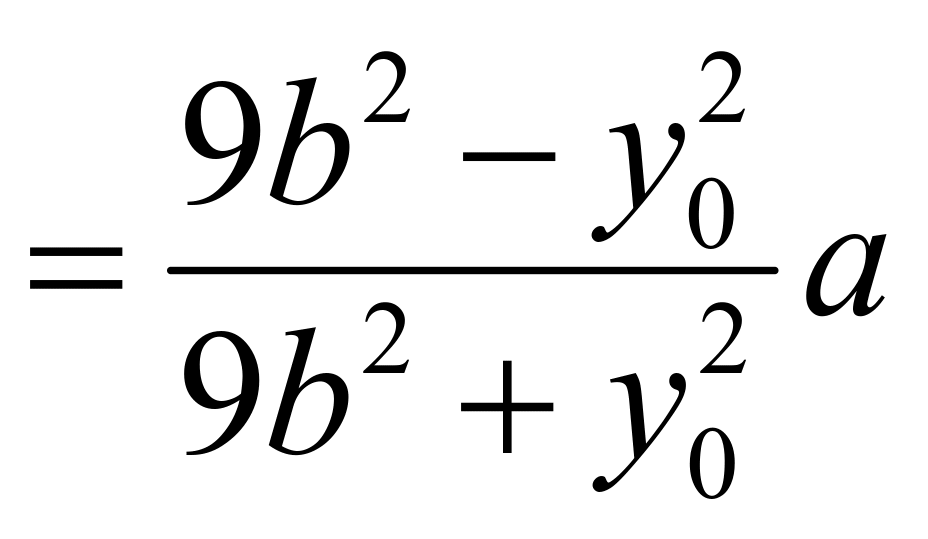 ,化简可知:
,化简可知:![]() ,所以
,所以![]() ,所以直线
,所以直线![]() 过点定点
过点定点![]() ,结论得证。
,结论得证。
结论推广
结论1中的![]() 在定直线
在定直线![]() 上,同样的将这条直线推广到一般情形
上,同样的将这条直线推广到一般情形![]() 中,则也有相应的结论,如下所示:
中,则也有相应的结论,如下所示:
结论2:已知![]() 为椭圆
为椭圆![]()
![]() 的左、右两个顶点,
的左、右两个顶点,![]() 为直线
为直线![]() 上动点,
上动点,![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,
,![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,则直线
,则直线![]() 过定点
过定点![]() 。
。
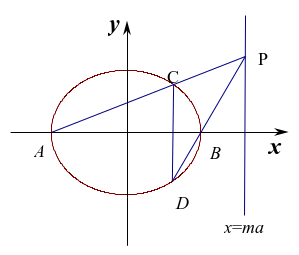
图3
证明:如图3:设![]() ,由题意可知
,由题意可知![]() ,
,![]() ,直线
,直线![]() 的方程为:
的方程为:![]() 将直线
将直线![]() 与椭圆
与椭圆![]() 联立
联立![]() ,通过化简可得:
,通过化简可得:![]()
![]() ,由于直线
,由于直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() ,根据韦达定理可知:
,根据韦达定理可知: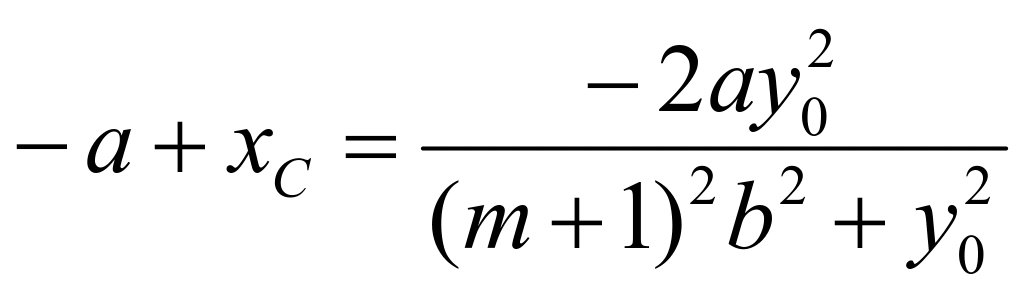 ,所以可知:
,所以可知: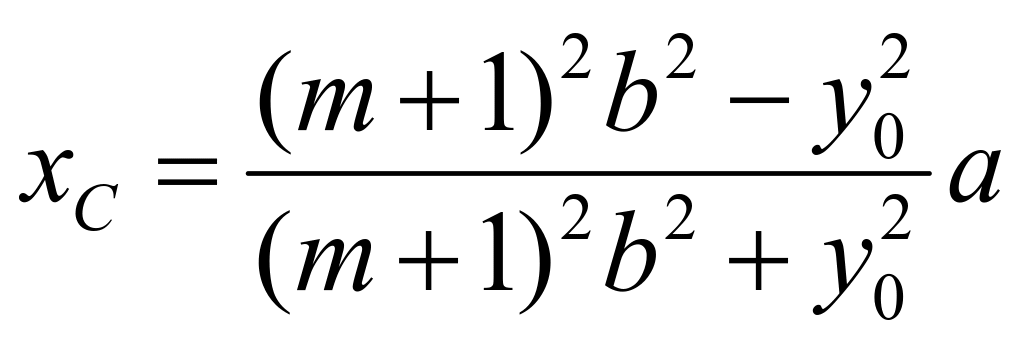 ,代入直线
,代入直线![]() 得
得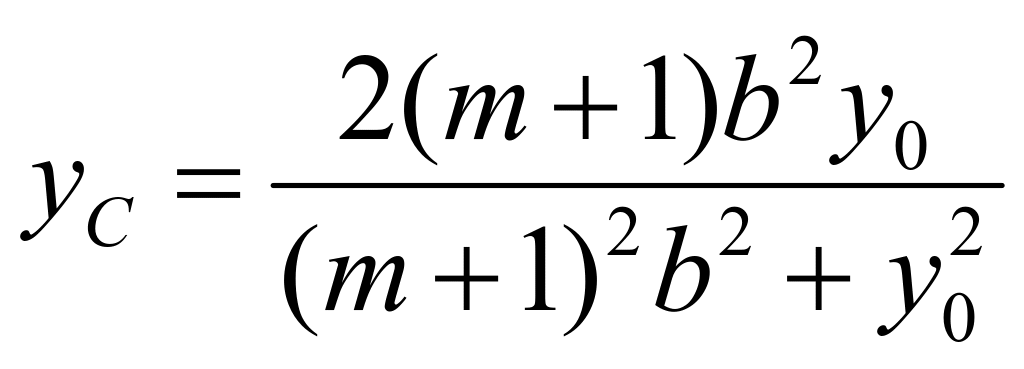 ,同理:直线
,同理:直线![]() 的方程为:
的方程为:![]() ,与椭圆
,与椭圆![]() 联立
联立![]() ,化简得:
,化简得:![]()
![]() ,由于直线
,由于直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() ,根据韦达定理可知:
,根据韦达定理可知: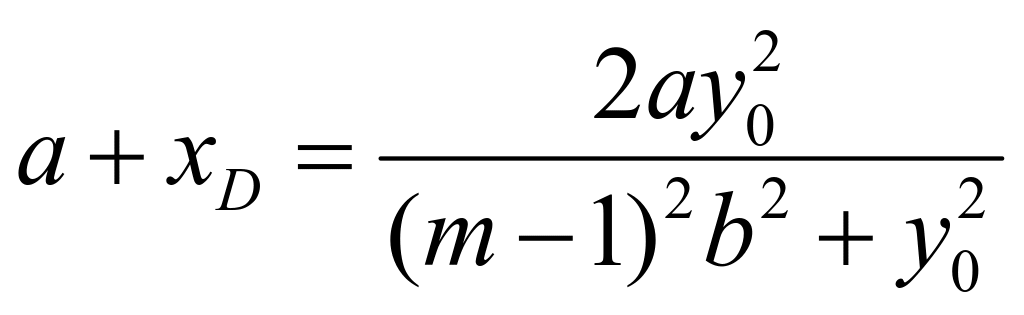 ,所以可知:
,所以可知: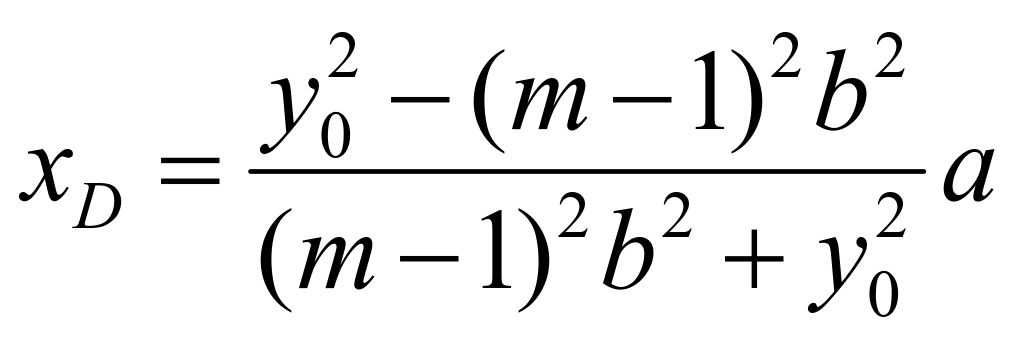 ,则
,则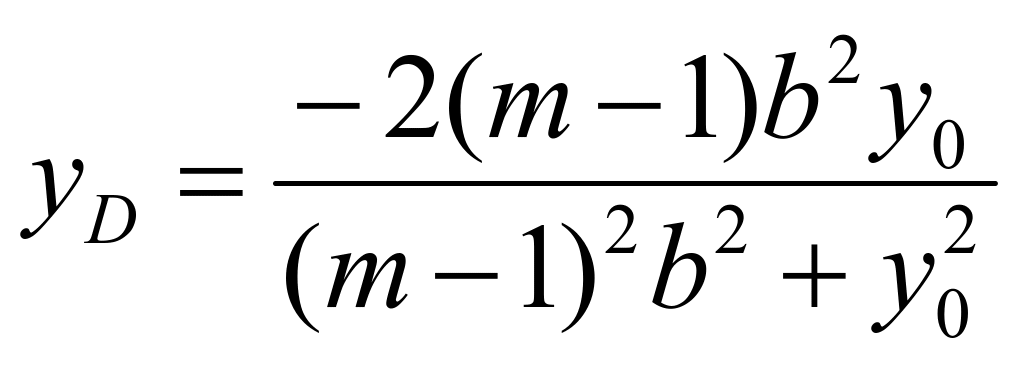 ,当直线
,当直线![]() 斜率存在时,根据两点式可以写出直线
斜率存在时,根据两点式可以写出直线![]() 方程:
方程:![]() ,化简得:
,化简得: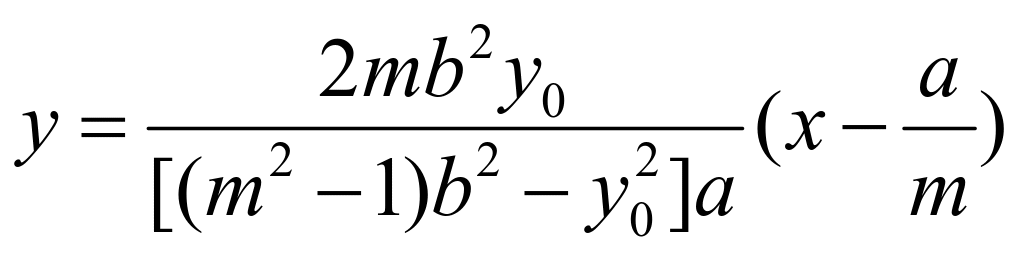 ,所以直线
,所以直线![]() 过点定点
过点定点![]() ;当
;当![]() 斜率不存在,
斜率不存在,![]()
![]() ,于是有
,于是有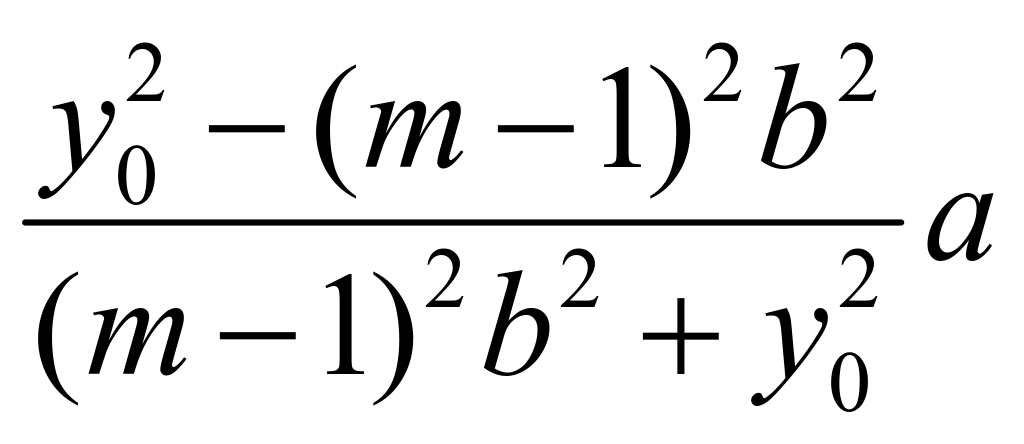
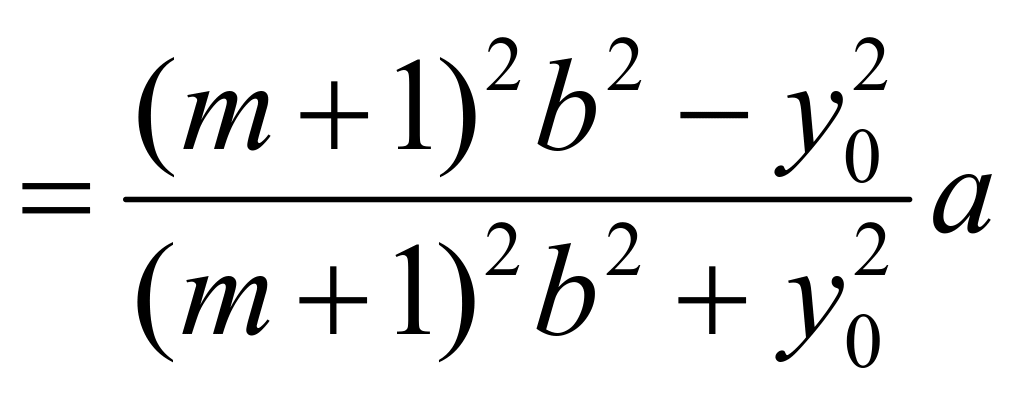 ,化简可知:
,化简可知:![]() ,所以
,所以![]() ,所以直线
,所以直线![]() 过点
过点![]() ,结论得证。
,结论得证。
注:上述结论中![]() 在定直线
在定直线![]() ,如果
,如果![]() 在定直线
在定直线![]() 上,则上述结论中的定点为:
上,则上述结论中的定点为:![]() 。
。
由上述的结论可以知道:结论2是建立在椭圆的连两个长轴上的顶点基础上得出的定点。将长轴上的两个顶点类比到短轴上的两个顶点也有类似的结论,如下所示:
结论3:已知![]() 为椭圆
为椭圆![]()
![]() 的上、下两个顶点,
的上、下两个顶点,![]() 为直线
为直线![]() 上动点,
上动点,![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,
,![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,则直线
,则直线![]() 过定点
过定点![]() 。
。
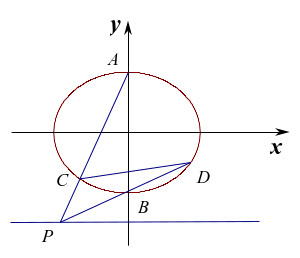
图4
注:证明过程与结论2类似,这里不再赘述。 类似于结论2,结论3中![]() 在定直线
在定直线![]() ,如果
,如果![]() 在定直线
在定直线![]() 上,则上述结论中的定点为:
上,则上述结论中的定点为:![]() 。
。
类比探究
直观想象圆与椭圆的特殊关系,设圆的方程为![]() ,将其变形可知
,将其变形可知![]() ,可以近似的认为圆是一个特殊的椭圆,即当
,可以近似的认为圆是一个特殊的椭圆,即当![]() 时的椭圆,因此上述结论在圆中也有类似的结论,如下所示:
时的椭圆,因此上述结论在圆中也有类似的结论,如下所示:
结论4:已知![]() 为圆
为圆![]() 与
与![]() 轴的左、右两个交点,
轴的左、右两个交点,![]() 为直线
为直线![]() 上动点,
上动点,![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,
,![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,则直线
,则直线![]() 过定点
过定点![]() 。
。
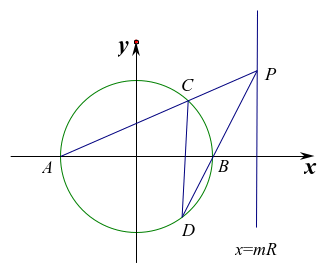
图5
注:证明过程与上述结论2的证明类似,只需要将上述过程中的![]() 替换成
替换成![]() 即可得到该结论,这里不再赘述。
即可得到该结论,这里不再赘述。
五、应用与思考
关于对2020全国Ⅰ卷的圆锥曲线压轴题题型的考查,在各地高考与模拟试题中均有考查(如:2010年江苏卷、2020年江苏盐城市三模),这体现了高考题常考常新的命题理念,如果教师在讲解往年高考题时,对这类问题进行探究与挖掘,引导学生进行深入思考,在高考中,学生处理起来会得心应手,事半功倍。
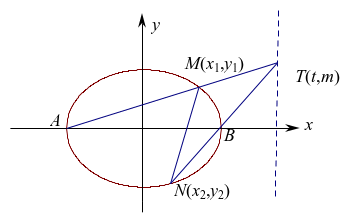
(2010江苏卷,18)在平面直角坐标系![]() 中,如图,已知椭圆
中,如图,已知椭圆![]() 的左、右顶点
的左、右顶点
为![]() ,右焦点为
,右焦点为![]() 。设过点
。设过点![]() (
(![]() )的直线
)的直线![]() 与椭圆分别交于点
与椭圆分别交于点![]() 、
、![]() ,其中
,其中![]() ,
,![]() 。
。
设动点P满足![]() ,求点P的轨迹,
,求点P的轨迹,
(2)设![]() ,求点T的坐标;
,求点T的坐标;
(3)设![]() ,求证:直线
,求证:直线![]() 必过
必过![]() 轴上的一定点(其坐标与
轴上的一定点(其坐标与![]() 无关)。
无关)。
注:利用结论2,我们知道![]() 在直线
在直线![]() 上,对应于结论2中
上,对应于结论2中![]() ,可知
,可知![]() ,对应于直线
,对应于直线![]() 过定点
过定点![]() 。即定点为
。即定点为![]() 。
。
探究圆锥曲线问题时,应注意探究的过程是循序渐进的过程,由特殊到一般的过程。本文首先从高考题入手,对条件进行一般化后得到结论1,然后在结论1的前提下将结论一般化,通过直观想象,将结论类比到圆上,教师在引导学生探究这类问题的一定要以培养学生的数学核心素养为目标,让学生参与探究的过程,使得学生产生探究学习的兴趣。
此外,教师更应该注重培养学生对这类问题的推导与证明的能力。“会而不对”、“思路有而做不出”等问题都是暴露学生的推理与证明的能力的缺陷,究其原因是学生数学运算素养的不够,而圆锥曲线的计算过程繁杂程度往往让学生望而却步,因而教师不仅仅要引导学生学会分析,更应该注重数学运算的核心素养的培养,还应该引导学生学会总结、归类与分析问题。
参考文献
[1]王开前. 一道圆锥曲线试题的解法探究与结论推广[J]。中学数学教学参考,2020(09):76-77。
[2]陈静静. 对改编一道圆锥曲线题的探究与反思[J]。数学教学通讯,2019(27):70-71。
6