基于互联网＋背景下数学课堂结构性的研究 ——以《多边形的内角和为例》

基于互联网＋背景下数学课堂结构性的研究 ——以《多边形的内角和为例》

强筱雪

常州市钟楼区西新桥小学 江苏省常州市 213000

解决的主要问题

在这节课之前我一直在思考两个问题：①我到底想通过平台突破传统课堂的哪些局限？②怎样在突破中建立方法模型、丰盈教学结构？

我选择使用珠峰平台进行教学，希望通过数字化学习方式突破以下几点：

1. 能进行高效不受空间限制的资源聚焦。

《多边形的内角和》内容是一次探索规律的活动，主要引导学生通过观察、操作、归纳、类比等具体的活动，发现多边形内角和的计算方法，需要学生进行大量的操作。学生在平板上的操作结果需要大量的进行展示，通过资源聚焦，无论是教室哪个角落的学生都能够清晰的看到同伴的思考。不会因为距离的远近产生偏差，同时资源展示也具有及时性。

2. 最大程度的进行同伴互助。

《多边形的内角和》是一节规律探索课，需要同伴之间进行大量的合作讨论。利用平台，学生提交资源后，能自主选择查看他人的解答，并给予点评，精彩的回答将会得到褒奖，劣势方法会得到建议，学生自然而然择善而从之。

同时，我希望在这样数字化的课堂中丰盈原有的课堂结构，达到如下的目标：

1. 学生在过程中建立清晰的数学空间与几何领域的学习方法模型。清晰的结构式学习可以帮助学生形成清晰的方法学习模型，同时借助于平台进行自主性的探索。

2. 在过程中，教师不断丰盈传统课堂的教学结构。数字化学习带来的变化应该是丰盈，而不是完全的破除重构和取代。教师在这样的课堂中进行不断探索，力求建立教学结构模型。

解决问题的过程与方法

一、常规积累：

回顾：

通过前面学习你对三角形有了什么了解？和你的同桌说说。

学生交流（让学生说，教师不要评价）

二、新课学习

呈现十二边形

师（出示问题1：十二边形的内角和是多少度？）：我们都知道了三角形的内角和是180度，你知道这个多边形的内角和是多少度吗？

师：有点难度了吧。回想一下这样复杂的问题，我们是怎样解决的？你在以前学习中有过这样学习经验吗？和你的同桌说一说。你来说说，其他同学还有补充吗？2名学生说完教师再最稳：有感觉吗？

师：复杂问题，我们可以从简单问题入手，慢慢的找到规律就可以来解决这个复杂问题了。这个十二边形我们可以先从边少一些的开始研究，最少几边形？三角形我们已经知道了内角和是180度，那我们从四边形开始研究。

1. 学习任务一：研究四边形

（出示学习任务一：请你对下面两个四边形进行研究，想办法求出四边形四个内角的和是多少度，锦囊中提供可移动测量的量角器）

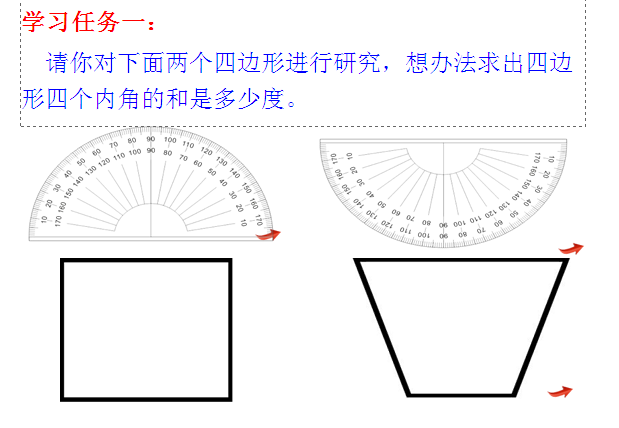
捕捉学生资源（长方形标上直角符号，量的标上度数的、分的）

（聚焦学生资源：标直角）

师：你看这位同学，你知道他是怎样求内角和的吗？想一想，自己说一说。

师：请这位同学来说说你的想法。

学生：每个角都是直角，所以内角和360度。

.师：这个同学利用长方形角的特点，一样就看出内角和是360度。

学生没有说到90度。师：这个长方形上什么都没有？你怎么知道的？（请学生说一说）

师：这个同学利用长方形角的特点，一样就看出内角和是360度。

（聚焦学生资源：量角器测量标记）

师：这位同学是怎样想的？学生交流 师：她是用量角方法得到了四边形内角和是360度。

总结：测量是一种基本方法，能让我们大约知道内角和是多少度，是不精确的。

（出示学生剪拼视频）

小结：同学们真棒，运用前面学过的图形的特征、剪拼、量方法得到了四边形内角和是360度。

师：还有同学这样来研究四边形的内角和的，我们一起来也来看一看。

（聚焦学生资源：用线分角）

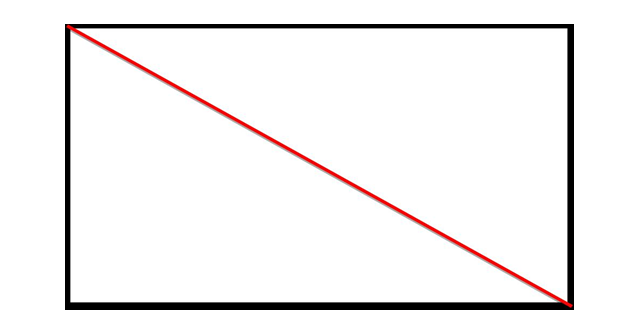
师：我们来看看这位同学的思考过程，她既没有量角、也没有剪拼，就用简单的一条线求出了四边形的额内角和，你知道他是怎样的，和你的同桌说说。

师：谁来说说，

学生交流（2人）

师：听明白他的想法了吗？（你再来说说）

生1：将四边形分为2个三角形，一个三角形内角和是180度，2个是2个180度。

师：简单的一条线就能得到四边形内角和的度数，这就是数学简洁之美。你也能像他那样用一条线把四边形分成两个三角形吗？在你的四边形上试试看。（学生操作）

师：刚刚是从顶点到顶点用一条直线将四边形分成2个三角形，四边形的内角和是2*180°（板书）想一想，分割的时候一定要从顶点到顶点吗？还可以怎么分割？请你在四边形上自己试试。

（聚焦学生资源：从边开始分割）

看看这位同学的，想一想现在四边形的内角和应该怎样计算？计算之前先标一标内角。

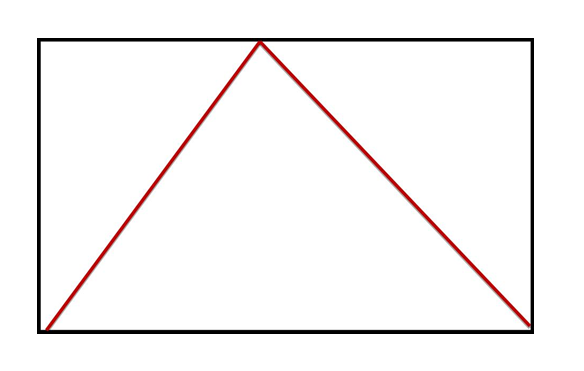
这位他同学是在图形哪边进行分割，这时候内角和应该怎么计算呢？

（聚焦学生资源：从图形中开始分割）

提炼：比较这些算式，你发现什么共同点？四边形的内角和都可以转化成两个三角形的内角和。

小结：我们刚才通过量角、分割的方法，把四边形分成了两个三角形，在分割是时候还发现：分割可以从顶点到顶点；可以从边上开始分割；还可以在图形中进行分割，它分出来的内角和都是360°（完成黑板上板书）

过渡：同学们真厉害，用不同方法得到了四边形内角和是360度，那我们用这些方法继续研究五边形的内角和。

1. 学习任务二：研究五边形

（出示：学习任务二：至少选择2个五边形，能不能用才发现的方法求出五边形5个内角的和是多少度，再与同桌交流。）

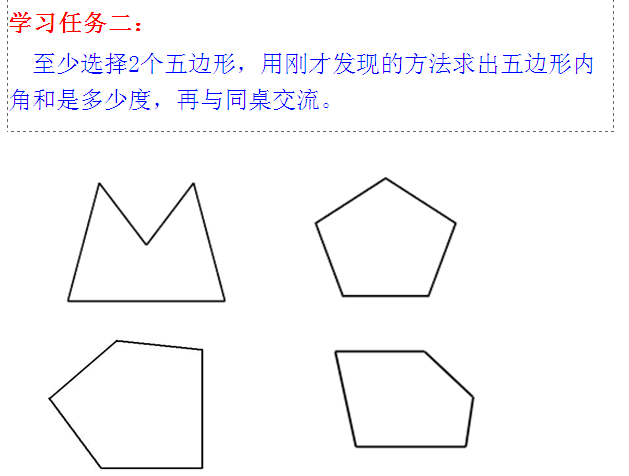
过程介入：师：我看到很多同学都是用分割的方法，为什么几乎没有同学用量角和剪拼的方法？

生：分的方法太麻烦了，剪的方法也很麻烦。

师：剪拼是不是真的麻烦，我们一起来看一下这个同学剪拼的过程，播放录像。

学生看了后，教师继续说：看来剪拼在这里还不能得到五边形内角和。

师：请同学们继续尝试在五边形上分一分。做完和同桌说一说。

（教师巡视，观察学生的操作过程，选择不同的形状呈现，正、任意、凹）

6．师：观察这些同学的研究过程，你发现什么?直接同学起来说。

请2人说说一说

小结：这些五边形都分成了3个三角形，所以内角和是180 乘3=。

师：刚才我们通过分割发现了三角形有3条边,1个三角形内角和是180°乘1，四边形有4条边分成2个三角形，内角和是180乘2，五边形有5条边分成了三个三角形，内角和是180 乘3，你觉得多边形内角和可能会和图形的什么有关？

过渡：师：到底对不对呢？是不是有关系呢？或者有什么样关系，一个科学结论需要有大量数据呈现，我们还需要继续研究，

（出示：学习任务三：四人小组，每人选择一种多边形快速研究一下内角和，做完后在小组里说说。）

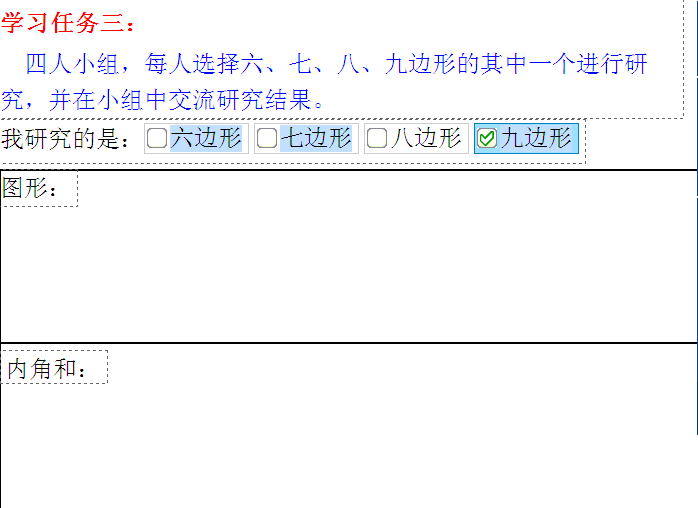
师：如果你能根据这些数据直接推想，那就写出你的猜想，然后在图形上验证你的猜想。如果不能，就像刚才一样先在多边形上研究它的内角和，看看有什么发现？为了研究方便，四人小组，每人研究一种多边形内角和，快速研究一下，做完后在小组里说说。

师：都研究好了吧，来说说你想的思考过程。

交流：六边形、七边形

六边形交流了，师：其他研究六边形是这样吗？

六边形，分成4个三角形，内角和180度乘4

七边形，分成5个三角形，内角和是180度乘4

7、师：通过刚才的研究我们发现：四边形分成2个三角形，五边形分成3个三角形，六边形分成4个三角形，七边形分成5个三角形，那十边形分成多少个三角形，内角和是多少度？你是怎么知道的？同桌说说。

｛聚焦学生资源：直接列式计算｝你的想法和他一样吗？到底是不是呢？让我们一起来看一下，一起来验证。

这里有一个十边形，数一数，分成几个三角形，内角和是？

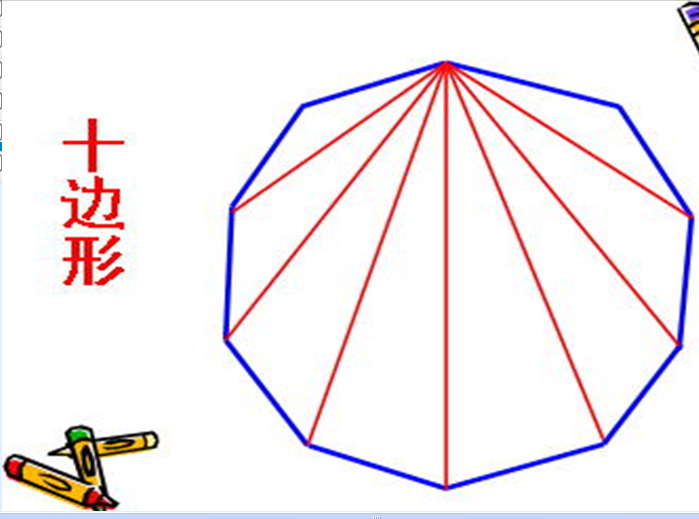
对吗。

8、师：如果照这样推想下去n边形内角和是多少度？你是怎样想的？和你的同桌说说。

交流：n边形能分成n－2个三角形，n边形内角和=180°×（n－2） （板书）

9、出示开始问题：现在这个复杂问题可以解决吗？十二边形内角和多少度？你是怎样想的？

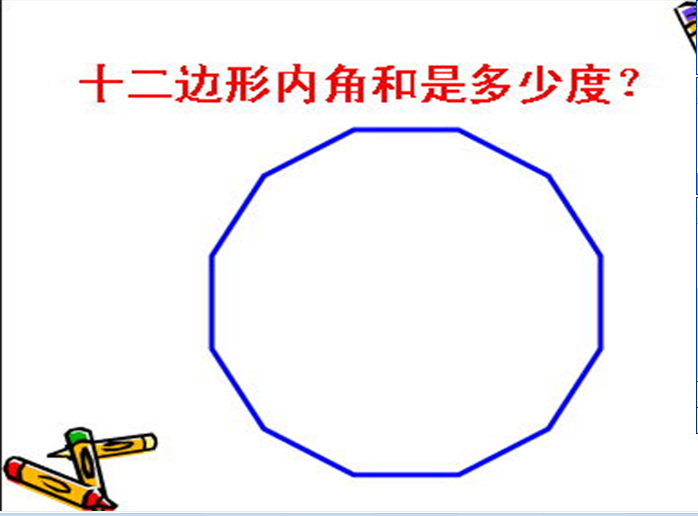
1. 3. 总结提升

1、回顾探索和发现规律的过程，说说你的体会。同桌互相说。（学生在讨论版上互相发言点评）

2、小结：今天这节课我们一起来研究了《多边形的内角和》规律（板书课题），我们把一个复杂的问题，先转化为简单的问题，找到规律后，再来解决复杂的问题。（板书）

\