在探究中合作学习 在活动中积累经验——圆周长的练习

在探究中合作学习 在活动中积累经验——圆周长的练习

马婷婷

巍山第一小学教育集团巍山校区 浙江 金华 322100

【设计理念】：练习课是比较枯燥的，但是在数学教学中练习课的所占比例又比较大。为了激发学生学习兴趣，提高学生学习的积极性。所以在设计圆的周长这节练习课时，我打破了原有的复习练习周长的题目，采用猫追老鼠引入，在这样的线路当中，猫应该选那条线呢？不仅激发了学生的兴趣，复习了圆的周长计算公式周长=圆周率×直径=2×圆周率×半径，后面又将图形变变变，通过这个探究活动，引导学生观察，猜想，丰富学生知识结构，深入反思，从而发展学生转化与化归、分类与讨论、推理、模型等数学思想方法。

【教学内容】：北师大六年级上册第一单元元的周长的练习课

【教学目标】：

1. 进一步理解周长、直径、半径之间的关系，能熟练运用圆周长公式来解决一些实际问题。
   2、培养学生分析问题和解决问题的能力，发展学生的空间观念。 
   3、感受平面图形的学习价值，进一步提高学习数学的兴趣和学好数学的信心。 
   【教学重、难点】：
   重点：理解周长、直径、半径之间的关系，能熟练解决一些实际问题。
   难点：提高综合应用圆周长知识和方法解决实际问题的能力。 

【教学过程】：

一、复习旧知，激活经验

师：同学们，前几节课我们学习了哪些知识？

预设：１.认识了圆的直径，半径，圆心确定位置，半径确定圆的大小

2. 圆的周长跟直径有关，圆的周长＝圆周率×直径

3. ……

师：下面我们就做一题有关圆周长的题目，请看（出示：一只猫在追赶一只老鼠，老鼠刚好跑过池塘。有①、②两条路，你认为猫走哪条路近一些？）

预设：

１.可能走①号路线，看着短一些

２.可能是②号路线，就像三角形两边之和大于第三边

３.两条路一样长，走那条都可以。

师：哪到底谁说的对的？（可以算一算）

设计意图：数学教学活动，特别是课堂教学应激发学生兴趣，调动学生的积极性。本环节的设计从回顾已学知识，到猫抓老鼠这一有趣情景，点燃学生的探索欲望。

二、讨论交流，初探规律

１.师：这两条路线该怎么求呢？（补充：起点到终点是一条直径，长度为８ｍ）

同桌互相讨论，教师巡视指导，指名汇报

预设：①３０➗２＝１５ｍ，３.１４×１５➗２×２＝４７.１ｍ

　　　②３０×３.１４➗２＝４７.１ｍ

　　　①＝②，两条路一样长

２.师：老师将这两条路变一变（出示），现在你觉得小猫应该走那条路？

　生独立完成，教师巡视指导，指名汇报

预
设：①３０×３.１４➗２＝４７.１ｍ

　　　②２０×３.１４➗２＝３１.４ｍ　　１０×３.１４➗２＝１５.７ｍ

　　　　　３１.４＋１５.７＝４７.１ｍ

①＝②，两条路一样长

3.师：观察刚刚的两题，并与同学交流，说一说你的发现？

学生小组内交流

4.交流发现，初步感知：在同一条直径中，分成2个小半圆时，大的周长等于里面小周长之和

师：通过刚才的两道题目，你有什么发现?

预设：小圆的周长之和等于大圆的……

师：很好的想法。那是不是所有的肯定一样吗？

设计意图：“数学活动的开展应该以学生的认知发展水平和已有的经验为基础。”从简单的，易于发现结论的图形开始，让学生在交流中体会成功的喜悦，也为后面的探究做好铺垫。这样的设计，就是让学生通过交流，计算很快发现大圆和小圆周长之间的关系，体验到成功的乐趣，也为下一环节树立信心。

三、再次探究，验证规律

师：在刚才的活动中同学们发现了一个规律，那么如果里面变成3个小圆或者4个呢？

①

②

C O

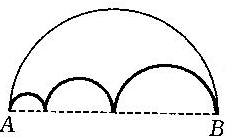
出示：如右图，线段AB是圆的直径12cm，AC是2cm，两条路线一样长吗？

师：从题目中你读懂了什么？

预设：里面有三个小半圆

o是圆心，AC是2cm，CO为4cm……

师：现在里面变成3个，它们还一样长吗？

师：实践是检验真理的唯一标准。你们的猜想是否正确呢？请动手算一算，验证一下。

生独立完成，师巡视指导

师：完成的同学前后同桌互相谈论一下。

交流，归纳：①12×3.14➗2=18.84cm

②2×3.14➗2=3.14cm （12➗2—2）×3.14➗2=6.28cm

12➗2×3.14➗2=9.42cm 3.14+6.28+9.42=18.84cm

①＝②，两条一样长

师：观察者三题，试想是不是在这一条直径里，无论分成分数个圆，他们的周长都一样长呢？

四、验证猜想，再探规律

师：请同桌两个同学为一组，画一画，算一算（里面可以是分成4个，5个，6个……），

学生尝试画一画，算一算，教师巡视指导

学生交流、反馈，归纳小结

小结：在同一条直径里，无论分成多少个小圆，外圈的周长等于里面小圆的周长之和。

设计意图：通过多层次的探究与观察，把思维推向更深层次。有了前两次的探究经验，下面的环节中的活动会非常顺利。所以，在活动开始前，先让学生猜想：“它们的长度是否一样？”以问题为载体，让学生自主的参与到活动中，让学生经历猜想，验证等活动过程，积累活动经验，提高学生的解决问题的能力，增强学习的信心。

五、运用规律，提高能力

师：经过刚才的学习与探索，我们发现了在同一条直径里，无论分成多少个小圆，外圈的周长等于里面小圆的周长之和。那你能运用学到的规律解决下面的问题m吗？

1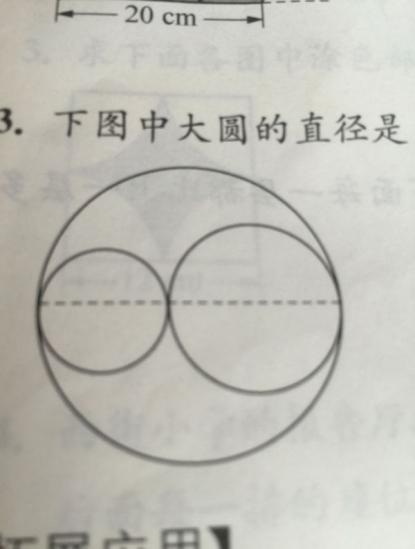 . 15cm，大圆和两个小圆之和的周长分别是多少？

2. 算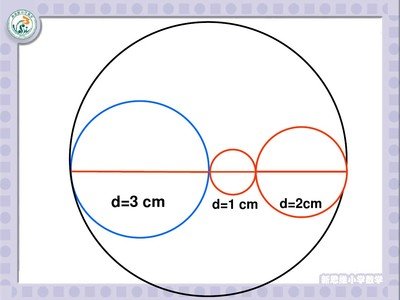 一算他们的周长之和

设计意图：数学源于生活又服务于生活，一个活动使学生明白数学知识的习得、数学经验的积累都是为了解决生活中的实际问题，，帮助学生树立正确的数学观，体现了数学本身的价值。

六、全课小结，畅谈收获

师：通过本节课的学习，你有什么收获？

本节课，我突破以往的复习，通过一题多变来进行圆周长的练习，首先第一题就是将直径原本是平均分成两份，感受它们的长度是否一样，接下来第二题直径只是随意分成两份，接下来又将直径变成3份，后来有让学生自由创造，让学生不断的解释，阐述，发现规律。学生经历了数学化的过程，满足了学生的心理需求。通过积极思考和合作交流得出规律，引发学生对数学思想、数学方法的体会和领悟。

课标中指出要让学生“在数学活动中积累经验”，活动的系统化有助于学生积累数学活动经验。从特殊到一般逐层归纳发现与验证是结论的常用发法。从探究活动中获得经验、积累经验，再次运用经验推理。本节课的数学活动，是让学生“发现”“再创造”数学知识，领悟思想方法，形成能力。由于题目有点难度，在教学时，我常常采用同桌交流的方式推进学生学习的过程。