北大附中云南实验
杨辉三角形,又称帕斯卡三角形、贾宪三角形、海亚姆三角形,它的排列形如三角形。因为首现于南宋杨辉的《详解九章算法》得名。在欧洲,因为法国数学家布莱兹‧帕斯卡在1653年的《论算术三角》中首次完整论述了这个三角形,故也被称作帕斯卡三角(Pascal's triangle)。人教版初中数学八年级下册第113页,阅读与思考中对杨辉三角进行了简单的介绍。
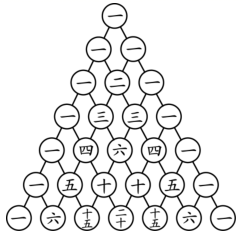
今天结合初中命题中会用到的情况进行分析,结合具体的题目利用杨辉三角的横行规律解题。
在初中数学上,杨辉三角的介绍和二项式展开式有关:

(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
……
二项式系数是二项式定理中各项的系数。而二项式系数可排列成杨辉三角,这样可以避免这样的麻烦,直接找到答案。
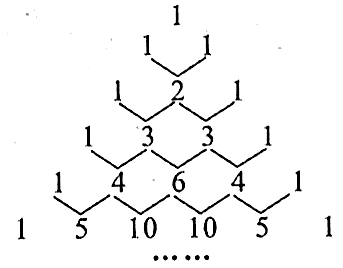
如何直接写出各项系数?
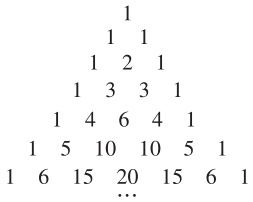
如图,在最上面一行的中央写下数字 1;第二行,写下两个 1,和上一行形成三角形;随后的每一行,开头和最后的数字都是 1,其他的每个数都是它左上方和右上方的数之和,就是说除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和。
一.利用杨辉三角的构建过程解题
例1.在学习整式乘法的时候,我们发现一个有趣的问题:将上述等号右边的式子的各项系数排成下表,如图:
(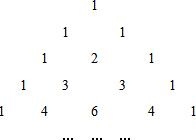 a+b)0=1
a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
这个图叫做“杨辉三角”,请观察这些系数的规律,直接写出(a+b)5=__________,并说出第7排的第三个数是___.
【答案】a5+5a4b+10a3b2+10a2b3+5ab4+b5;15.
【解析】根据杨辉三角的构建:把第6行写出来:

得到:(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
再借助规律写出第7行:1 5 15 20 15 6 1,故第三个数是
二、杨辉三角的横行个数及数字和规律
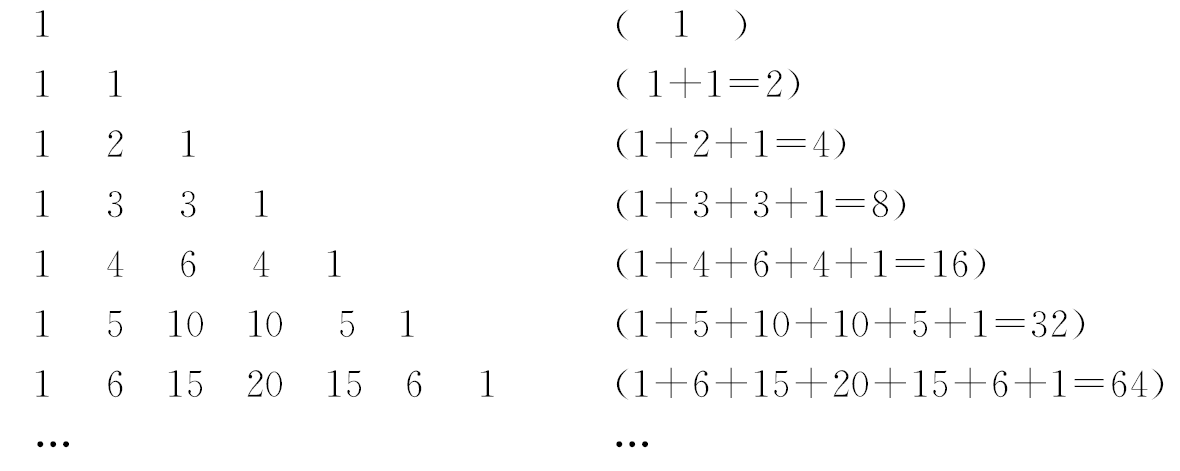
①横着每一行都有对应数字个数,第一行1个数,第二行2个数,第三行3个数,……
②横着每一行数字相加得到:a1=1=20,a2=2=21,a3=4=22,…,an=2n-1.
例2.我们知道(a+b)n展开式中的各项系数依次对应杨辉三角第 行中的每一项,如图给出了“杨辉三角”的前7行,请你按照这个规律,直接写出
行中的每一项,如图给出了“杨辉三角”的前7行,请你按照这个规律,直接写出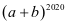 展开式共有______项,展开式的系数和是_______.
展开式共有______项,展开式的系数和是_______.
【答案】2021;22020.
【解析】由于第一行对应的是(a+b)0,所以(a+b)2020对应的第2021行,所以共有2021项;展开式系数和为22020.
三、巧设未知数的值求展开式系数和
当二项式的a,b有了具体的式子时,系数和就不仅仅时杨辉三角横行之和,这时巧设未知数的值可解决问题。
例3.我们知道,很多数学知识相互之间都是有联系的.如图,图一是“杨辉三角”数阵,其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和;图二是二项和的乘方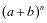 的展开式(按b的升幂排列).经观察:图二中某个二项和的乘方的展开式中,各项的系数与图一中某行的数一一对应,且这种关系可一直对应下去.将
的展开式(按b的升幂排列).经观察:图二中某个二项和的乘方的展开式中,各项的系数与图一中某行的数一一对应,且这种关系可一直对应下去.将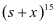 的展开式按x的升幂排列得:
的展开式按x的升幂排列得: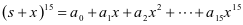 .
.
图一
| 图二
… … |
依上述规律,若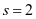 ,则
,则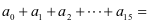 __________.
__________.
【答案】315.
【解析】(s+x)15=a0+a1x+a2x2+…+a15x15.
当x=1,s=2时,a0+a1+a2+…+a15=(2+1)15=315.
四、杨辉三角中隐含的11 的幂
杨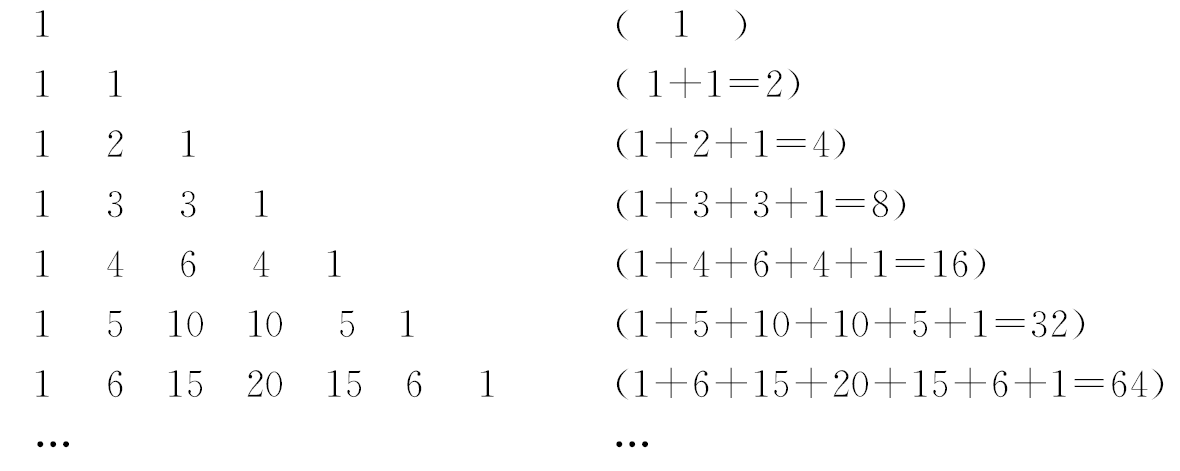 辉三角还揭示了 11 为底的幂的值。如图,将每一行的数字挤压到一起,前 5 行直接得到,第六行将十位数加到它左侧数字上,
辉三角还揭示了 11 为底的幂的值。如图,将每一行的数字挤压到一起,前 5 行直接得到,第六行将十位数加到它左侧数字上,![]() ,
,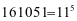 ,如果出现了三位数同样进位处理即可。
,如果出现了三位数同样进位处理即可。
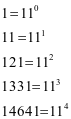
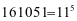
…
例4.杨辉三角是一个由数字排列成等腰三角形数表,一般形式如图所示,其中每一横行都表示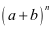 (此处
(此处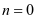 ,
,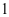 ,
,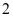 ,
,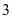 ,
,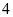 ,
,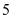 ,
,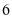 )的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字
)的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字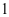 组成的,而其余的数则是等于它“肩”上的两个数之和.
组成的,而其余的数则是等于它“肩”上的两个数之和.
(1)从第二行到第五行,每一行数字组成的数(如第三行为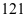 )都是上一行的数与_____积.
)都是上一行的数与_____积.
(2)由此你可写出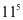 =_________________.
=_________________.
【答案】11,161051.
【解析】观察图表寻找规律:三角形是一个由数字排列成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和.
(1)11,121=11×11,1331=121×11,14641=1331×11,15101051=14641×11,
(2)11 5=(10+1) 5=10 5+5×10 4×1+10×10 3×1 2+10×10 2×1 3+5×10×1 4+1 5=161051,
针对性训练:
1.如图,为杨辉三角的一部分,它的作用是指导读者按规律写出形如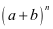 (
(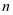 为正整数)展开式的系数,请你仔细观察下列等式中的规律,利用杨辉三角解决下列问题.
为正整数)展开式的系数,请你仔细观察下列等式中的规律,利用杨辉三角解决下列问题.
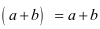
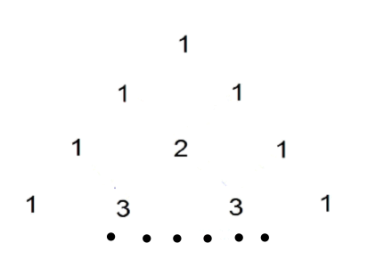
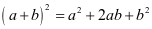
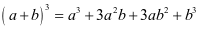
(1)填出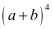 展开式中第二项是_________.
展开式中第二项是_________.
(2)求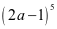 的展开式;
的展开式;
(3)计算: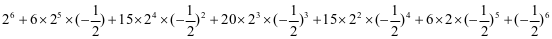 .
.
解:(1)由题意可得:(a+b)4=a4+4a3b+6a2b2+4ab3+b4;
(2)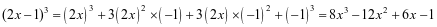 ;
;
(3)原式=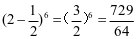
2.利用“杨辉三角”展开(1﹣3x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,那么a1+a2+a3+a4+a5=( )
A.0 B.1 C.-32 D.﹣33
【答案】D.
【解析】(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
因为有具体的a,b数值,故当x=1时(1-3)5=a0+a1+a2+a3+a4+a5,故a0+a1+a2+a3+a4+a5=(-2)5=-32.
因为a0=15=1,所以:a1+a2+a3+a4+a5=-32-1=-33.