BFRP筋钢纤维梁正截面开裂荷载计算

BFRP筋钢纤维梁正截面开裂荷载计算

邹家伟

重庆交通大学 重庆市 400000

摘要：目前规范只给出了结合材料力学的简化开裂弯矩计算公式，并且由于BFRP筋材料的特殊性，即使国外某些规范给定BFRP筋混凝土梁开裂荷载的计算公式仍然使用普通钢筋混凝土梁的开裂荷载公式计算。本论文在10根BFRP筋钢纤维混凝土梁的试验情况下，对开裂荷载进行计算公式的推导。

关键词：BFRP筋、开裂荷载、理论推导

1，BFRP筋钢纤维混凝土梁开裂后，受拉区混凝土进入屈服阶段，同时，钢纤维混凝土受压区仍成弹性阶段，故受拉区混凝土分为两部分，一部分是已经进入塑性阶段的混凝土，应力图形简化为矩形，另一部分为弹性部分，应力图形简化为三角形，开裂时应力应变简化模型见下图 4-1，由第三章可得，其截面应变基本符合平截面假定。

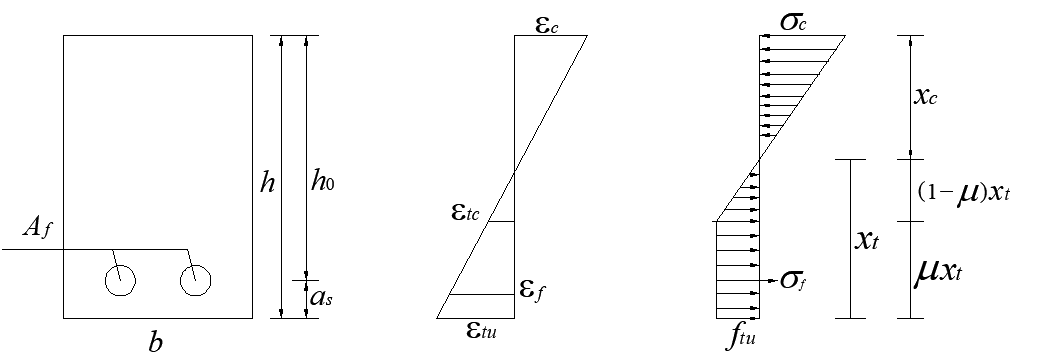图4-1开裂时应力应变简化模型

图4-1中， 、 和 分别为BFRP筋钢纤维混凝土梁的宽度、高度和有效高度， 为纵向筋材的截面面积， 为纵筋的合力到梁底部的距离， 为结构开裂时受压区的压应变， 为峰值拉应变， 为极限拉应变， 为受拉区混凝土开裂时BFRP筋拉应变， 为受拉区开裂时对应的受压区的压应力， 为开裂时的截面受压区高度， 为开裂时受拉区的高度， 为开裂时受拉区塑性发展程度系数， 为开裂时塑性发展高度， 为开裂时弹性发展高度， 为钢开裂时对应的纵筋拉应力， 为混凝土的抗拉强度，其取值通过第二章可得， ， 为钢纤维混凝土立方体抗压强度。

通过图4-1中应力应变模型可得：

开裂时受压区混凝土合力 ：

（4-1）

根据平截面假定可得：

（4-2）

通过（4-1）和（4-2）可得：

（4-3）

则受压区钢纤维混凝土合力对中性轴的弯矩 为：

（4-4）

受拉区钢纤维混凝土弹性部分的合力 为：

（4-5）

则受拉区钢纤维混凝土弹性部分对中性轴的弯矩 为：

（4-6）

受拉区钢纤维混凝土塑性部分的合力 为：

（4-7）

则受拉区钢纤维混凝土塑性部分对中性轴的弯矩 为：

（4-8）

受拉区混凝土开裂时纵筋的合力 为：

（4-9）

根据平截面假定可得：

（4-10）

由（4-9）和（4-10）可得：

（4-11）

令纵向FRP筋的弹性模量与钢纤维混凝土的弹性模量之比为 ，由此可得简化 为：

（4-12）

则纵筋合力对中性轴的弯矩 为：

（4-13）

由应力应变模型可得：

（4-14）

根据力的平衡条件可得：

（4-15）

将（4-3）、（4-5）、（4-7）、（4-12）和（4-14）代入（4-15）即可得：

（4-16）

上式为（4-16）中，通过化简并对 进行一元二次方程式求解可得：

（4-17）

根据求根公式即可得：

（4-18）

式中 ， ，

通过力的平衡关系可得钢纤维混凝土开裂弯矩：

（4-19）

将（4-4）、（4-6）、（4-8）、（4-13）和（4-14）代入（4-19）即可得：

（4-20）

令 ， 为弹塑性抵抗矩， 为受拉区混凝土的抗拉强度，通过（4-20）可得 为：

（4-21）

为了更好的符合规范的计算样式，通过钢纤维混凝土截面抵抗矩塑性影响系数对推导的公式进行简化，根据材料力学的计算方法计算梁的开裂弯矩值，即：

（4-22）

由（4-21）和（4-22）可得截面抵抗矩塑性影响系数 为：

（4-23）

式中 为将构件中纵向FRP筋换算为钢纤维混凝土面积后的截面抵抗矩，其值要基于等效原则，根据材料力学中关于截面面积的换算方法求得，换算后的截面面积 为：

（4-24）

通过面积矩相等的原则求得 即：

（4-25）

解得 ：

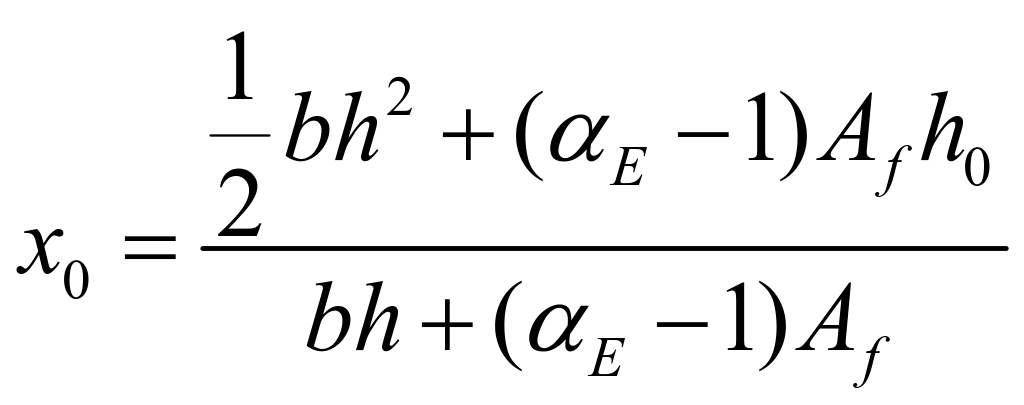（4-26）

换算的截面对形心主轴的惯性矩 为：

（4-27）

将式（4-27）和（4-28）代入（4-29）即可得：

（4-28）

本论文通过试验中测得和观察得到的开裂弯矩来计算塑性发展系数，参考第三章关于BFRP筋钢纤维混凝土梁的位移曲线分析图和试验梁加载过程中观察可得到的各构件开裂荷载下换算成开裂弯矩的值如下表4-1。

表4-1 试验梁的开裂荷载大小

将表4-1中开裂荷载大小计算成开裂荷载，由实测开裂弯矩值 ，通过下式（4-29）可以计算得出FRP筋钢纤维混凝土梁截面实测抵抗矩塑性影响系数 ，本论文使用迭代计算的方法进行计算，对 设定一个较小的初始值，然后求得A、B和C的值以及 和 ，并通过式（4-30）可以求出 ，求得值如果与 相差比较大，增大 的值重新计算，直到 和 的差值不大于0.01时，输出 ，结果见表4-2和表4-3。

（4-29）

（4-30）

表4-2 试验梁的塑性发展系数和抵抗矩影响系数

2 开裂弯矩的计算

通过程序框图输出的结果可得钢纤维混凝土开裂时受拉区塑性发展程度系数 ,截面抵抗矩塑性影响系数 和弯矩值 ，结果见表4-2。根据本章的试验结果，考虑钢纤维的体积率和结构构件的配筋率通过MATLAB软件对开裂塑性系数 进行拟合分析可得：

（4-31）

式（4-31）中， 为梁的配筋率， 为钢纤维体积率。将（4-31）拟合得到的开裂塑性系数 代入到式（4-22）得到的计算开裂弯矩值 与实测开裂弯矩值 进行对比分析验证。拟合后的值与实测值之比，平均数为1.01，标准差为0.034，变异系数为0.04.为说明计算程序算出的结果拟合后与实测值正确性较高。

依据 的大小，本节绘制出当构件开裂时受拉区混凝土塑性区和弹性区的应力分布情况。

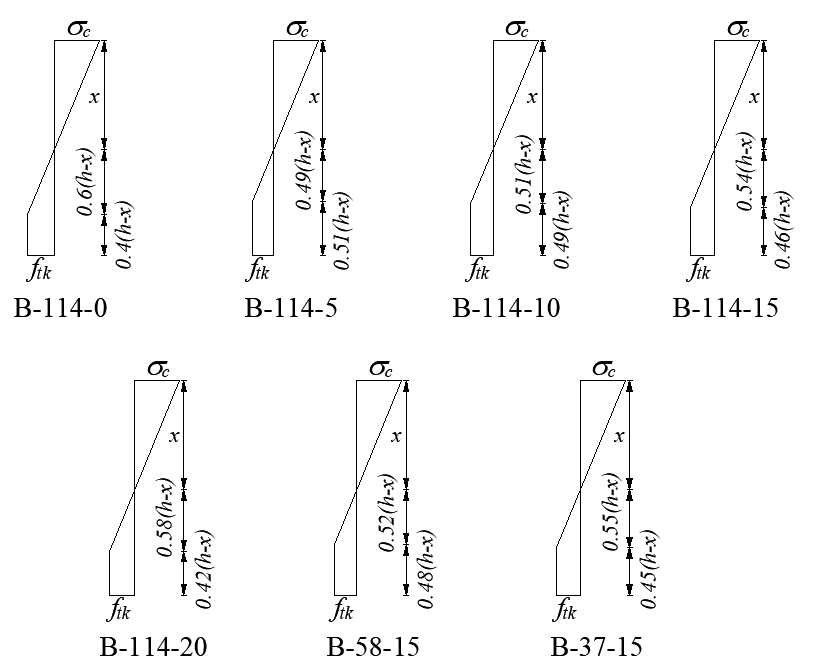
图4-2 试验梁的应力分布

从图4-2试验梁应力分布可得：当 值越大，其混凝土受拉区塑性区所占面积比就越大，证明塑性变形能力就越强，结合试验数据可以把 作为塑性变形能力的标准。结合表4-2和图4-3分析出，同样配筋率作用下，普通FRP筋混凝土梁在掺入钢纤维后，其塑性变形能力有所提高，且FRP筋钢纤维混凝土梁的塑性变形能力随着钢纤维体积率的提高而成减小的趋势，主要原因在于钢纤维的掺入提高了混凝土的强度，因而塑性发展能力变小。相同钢纤维体积率作用下的FRP筋混凝土梁由于配筋率的不同，其受拉区塑性变形的能力随配筋率的减小而减弱。根据试验梁的劈拉强度和塑性变形发展程度系数 来看，其两种发展规律都不一样，并不是开裂弯矩唯一决定的因素，应该是两种因素共同的作用。