1 云南省元谋县交通运输局 楚雄元谋 651300 ; 2. 云南红河州地方公路管理处 云南 红河 661100 ; 3. 云南交通职业技术学院 云南 昆明 650500
摘要:基于石灰改良高液限土试验路段的现场试验,采用多元非线性回归模型对填土层的压实度进行研究,分析了填土层的松铺厚度、填料的含水率、振动碾压遍数对压实度的影响,同时分析了填土层的松铺厚度、填料含水率、压实度对振动碾压遍数的影响,所得结果对石灰改良高液限土路堤填筑施工有指导意义。
关键词:高液限土;石灰改良;路基碾压;现场试验;多元非线性回归
中图分类号:TU443 文献标识码A 文章编号
。
0引言
在参考不限于文末所列参考文献后,针对石灰改良高液限土路基的压实工艺开展研究,通过现场碾压试验,分析石灰改良高液限土的松铺厚度、含水率、振动碾压遍数,对填土的压实度的影响,进而建立压实度与三个参数、以及振动碾压遍数与其它三个参数的多元非线性回归模型,以指导路基碾压工作。
1试验
1.1 概况
通过对高液限土取样并且进行室内相关试验,其基本物理力学指标见表1。
采用石灰对高液限土进行改良处理。石灰为外购熟石灰精粉,其化学成分为:CaO含量为73%,MgO含量为7.0%,为III级钙质石灰。通过无侧限抗压强度试验,确定石灰最佳掺加量为6%。通过击实试验得到石灰改良高液限土的最佳含水率为![]() 、最大干密度为
、最大干密度为![]() 。
。
表1 高液限土样的基本物理力学指标
含水率/% | 液限/% | 塑限/% | 最佳含水率/% | 最大干密度/ | CBR/% | 直剪 | 颗粒分析/% | 活动度/% | |||
| | >0.075mm | 0.075~0.002mm | <0.002mm | |||||||
27.0 | 61.0 | 28.0 | 17.0 | 1.68 | 3.1 | 29.0 | 28.0 | 26.5 | 58.9 | 14.6 | 2.26 |
1.2试验方案
(1)现场试验采用分层试验方法,每一填土层分别控制填料的松铺厚度h、含水率w,然后根据振动碾压遍数n,检测压实度K。
(2)每一层石灰改良高液限土填料的松铺厚度不大于30 cm,控制填料的含水率不超过最佳含水率的±3%。
(3)对于每一填土层,首先采用推土机整平,静压一遍后再振动碾压,达到所需要的压实度后再静压一遍收光。试验计量振动碾压遍数。
(4)振动碾压3遍后开始检测压实度。
(5)检测频率为每层平均分布4个点,松铺厚度h、含水率w、压实度K等每项检测内容取其平均值。
2试验结果与分析
2.1压实度检测结果
现场碾压试验共开展了12个填土层的试验,每一填土层的压实度检测结果见表2。
表2 压实度检测结果
松铺厚度/cm | 含水率/% | 振动碾压遍数/遍 | ||||
3 | 4 | 5 | 6 | 7 | ||
20 | 14.5 | 91.0 | 94.3 | 97.0 | 98.0 | 98.6 |
17.0 | 90.0 | 93.0 | 95.8 | 97.0 | 98.1 | |
19.6 | 90.5 | 93.0 | 95.8 | 96.2 | 97.2 | |
23 | 15.0 | 89.9 | 92.8 | 95.4 | 97.1 | 97.9 |
17.0 | 89.5 | 92.4 | 95.4 | 96.5 | 97.8 | |
19.0 | 89.2 | 91.5 | 93.5 | 95.0 | 96.5 | |
26 | 14.2 | 88.8 | 91.2 | 93.8 | 96.2 | 97.2 |
17.5 | 89.0 | 91.8 | 95.0 | 96. | 97.4 | |
20.0 | 87.9 | 90.0 | 91.1 | 93.8 | 95.8 | |
30 | 15.0 | 87.9 | 91.7 | 93.0 | 94.8 | 97.0 |
18.0 | 88.0 | 91.1 | 92.6 | 95.6 | 96.8 | |
19.8 | 87.0 | 90.1 | 91.6 | 92.6 | 93.8 | |
2.2试验结果分析
(1)含水率w对压实度K的影响
根据表2中的试验结果,石灰改良高液限土填料的施工含水率只要控制在最佳含水率±3%以内,相应的振动碾压遍数下对压实度的影响较小。
(2)松铺厚度h对压实度K的影响
松铺厚度h对压实度K的影响可近似为幂函数关系,回归关系式见表3。
表3 松铺厚度h与压实度K的回归关系式
振动碾压遍数/遍 | 松铺厚度h与压实度K的回归关系式 |
3 | |
4 | |
5 | |
6 | |
7 | |
(3)振动碾压遍数对压实度的影响
振动碾压遍数n对压实度K的影响同样可近似表现为幂函数关系,回归关系式见表4。
表4 振动碾压遍数n与压实度K的回归关系式
松铺厚度/cm | 含水率/% | 振动碾压遍数n与压实度K的回归关系式 |
20 | 17.0 | |
23 | 17.0 | |
26 | 17.5 | |
30 | 18.0 | |
(4)压实度与松铺厚度、含水率、振动碾压遍数的相关关系
根据表2中的压实度试验结果,采用多元非线性回归分析可以建立松铺厚度h、含水率w、振动碾压遍数n,与压实度K的相关关系。该多元非线性回归模型可表示为:![]() 。根据表2中的试验数据,该多元非线性回归模型为:
。根据表2中的试验数据,该多元非线性回归模型为:
![]() (1)
(1)
对式(1)的回归结果进行检验:相关系数![]() ,经F检验,
,经F检验,![]() >
>![]() 56)
56)![]() 。表明回归显著,即松铺厚度h、含水率w、振动碾压遍数n,与压实度K具有很强的相关性。
。表明回归显著,即松铺厚度h、含水率w、振动碾压遍数n,与压实度K具有很强的相关性。
为了检验回归效果,采用式(1)对表2中的数据进行回判,并将压实度的计算值与实测值进行对比,对比结果如图1所示。压实度的计算值与实测值的最大误差为1.62%。
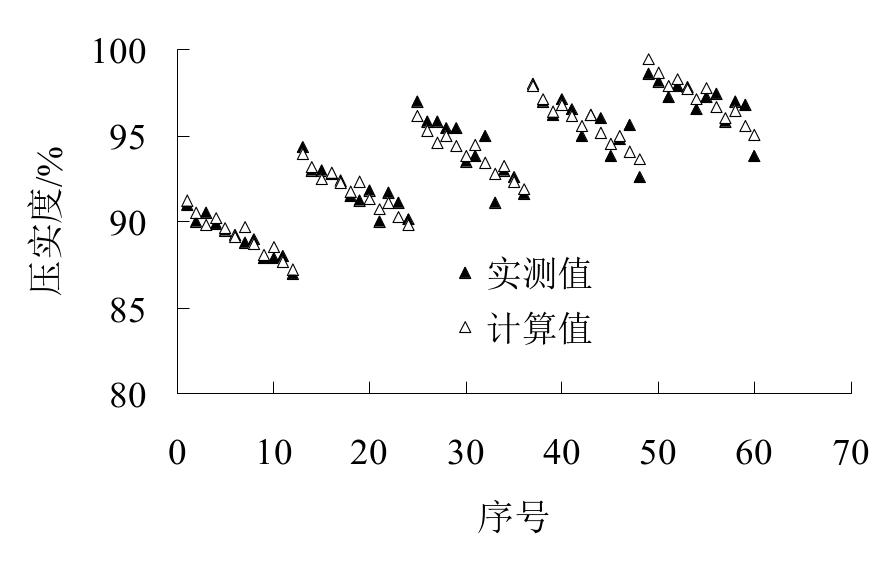
图1 压实度的计算值与实测值对比曲线
3振动碾压遍数的多元非线性回归模型
根据式(1),当填土层的松铺厚度h、含水量w确定后,可以根据振动碾压遍数n预测出填土层的压实度K。例如,当![]() cm、
cm、![]() %、
%、![]() ,则可预测出压实度为
,则可预测出压实度为![]() 94.2%。
94.2%。
路基碾压过程中,如果能够根据填土层的松铺厚度h、含水量w,以及填土层所处压实区所需要的压实度K,然后预测出振动碾压所需要的遍数n,这样就可对整个填方填筑工程进行公式化控制,减少施工控制的盲目性、加快施工进度,并且最大限度减少检测人员的工作量,提高检测效率。
基于此,根据表2中的压实度试验结果,采用多元非线性回归分析建立松铺厚度h、含水率w、压实度K,与振动碾压遍数n的相关关系。该多元非线性回归模型可表示为:
![]() (2)
(2)
对式(2)的回归结果进行检验:相关系数![]() ,经F检验,
,经F检验,![]() >
>![]() 56)
56)![]() 。表明回归显著,即松铺厚度h、含水率w、压实度K,与振动碾压遍数n具有很强的相关性。
。表明回归显著,即松铺厚度h、含水率w、压实度K,与振动碾压遍数n具有很强的相关性。
4结论
通过石灰改良高液限土路基试验路段的碾压试验,分析了松铺厚度、含水率、压实度、振动碾压遍数之间的相关关系,得到如下结论:
(1)分析压实度与松铺厚度、含水率、振动碾压遍数之间的关系,石灰改良高液限土填料的含水率如果控制在最佳含水率的±3%以内,对填土层压实度的影响较小。而石灰改良高液限土填料的松铺厚度、振动碾压遍数与压实度成幂函数关系[1]。
(2)采用多元非线性回归分析,建立压实度与松铺厚度、含水率、振动碾压遍数之间的相关关系表达式。根据该表达式计算得到的压实度与现场试验的实测值可较好吻合。
(3)根据现场试验结果,建立了松铺厚度、含水率、压实度,与振动碾压遍数之间的多元非线性回归模型。该模型预估的振动碾压遍数与实测值同样可较好吻合[2-3]。
参考文献:
[1]JTG D30-2015,公路路基设计规范[S]. 北京:人民交通出版社,2015.
JTG D30-2015,Specifications for Design of Highway Subgrades[S]. Beijing:China Communication Press,2015.
[2]万钰菊. 生石灰处治高液限土的研究与应用[J]. 北方交通,2016,(7):128-131.
[3]杨和平,李宏泉. 石灰改良处治高液限土的路用特性试验研究[J]. 公路工程,2013,38(4):227-229.