小学数学数形结合思想的渗透与应用

小学数学数形结合思想的渗透与应用

付彬

湖南省娄底市第一小学 湖南 娄底 417000

为了顺应新课程改革，发展学生的核心素养，使学生具备终生发展和社会发展需要的必备品格和关键能力。在新的教育课程改革中有着对许多科目的新要求，以及对教育教学方式的新要求。对于数学教学来说，培养学生的数学核心素养就是培养学生终生发展必需的数学综合能力，“学会数学思考”。《义务教育数学新课程标准2011版》中明确提出10个核心素养。其中数学里的数形结合思想的渗透对核心素养中的数学建模、几何直观等素养的培养具有重要的意义。

1 数形结合思想，贯穿小学教学的始终

数形结合思想是小学数学中最常见，应用最广泛的数学思想，把数与形结合起来解决问题可使复杂的问题变得更简单，使抽象的问题变得更直观。数形结合的例子在小学数学教材与教学中比比皆是。有时候是图形中隐含着数的规律，可运用数的规律来解决图形的问题。有时候是利用图形来直观地解释一些比较抽象的数学原理与事实，让人一目了然，尤其是小学生的抽象思维程度还不够高，经常需要借助直观模型来帮助理解。例如用长方形模型来教学分数乘法的算理，利用线段图来帮助学生理解分数除法的算理。利用面积模型来解释两位数乘两位数的算理、乘法分配律、完全平方公式等，利用正比例关系和反比例关系图像帮助理解正比例与反比例关系式。

数与形密不可割，可用形来帮助理解数，也可用数来解决形的问题。如用数来解释图形的规律，再依规律解决问题。如下图，摆1个三角形需要3根小棒，摆2个三角形需要5根小棒……按照这样的规律，摆5个三角形需要（ )根小棒，摆n个三角形需要( )根小棒。

在数论，数量关系式，位置与方向，统计等教学中无不渗透着数形结合的思想（如下图）

数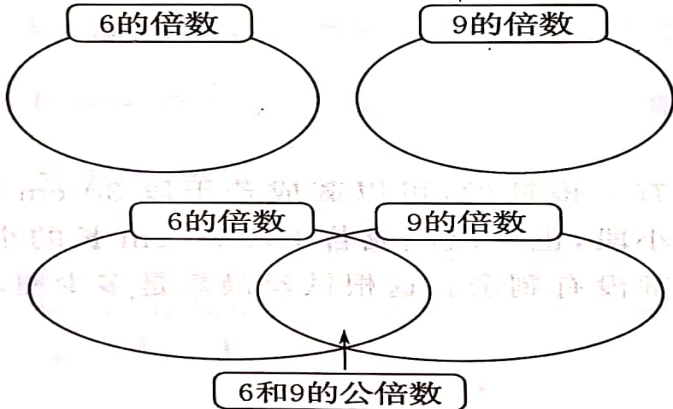 论：

1、3是6和9公有的因数，叫做它们的公因数。

其中3是最大的公因数，叫做它们的最大公因数，

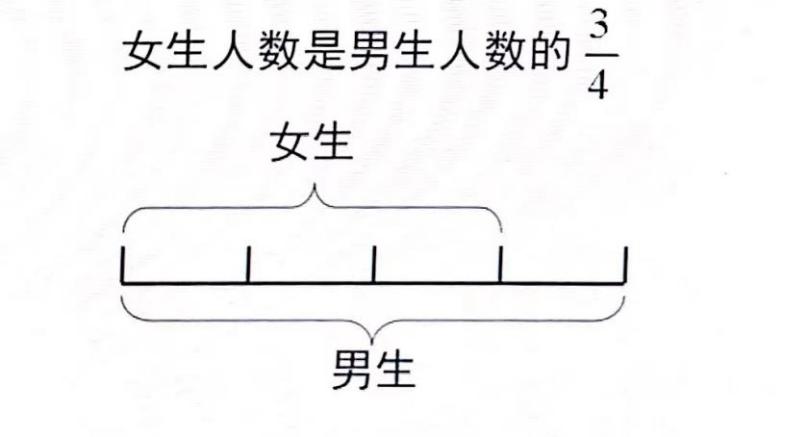
数量关系：利用线段图表示女生人数是男生的3/4这样一种数量关系：

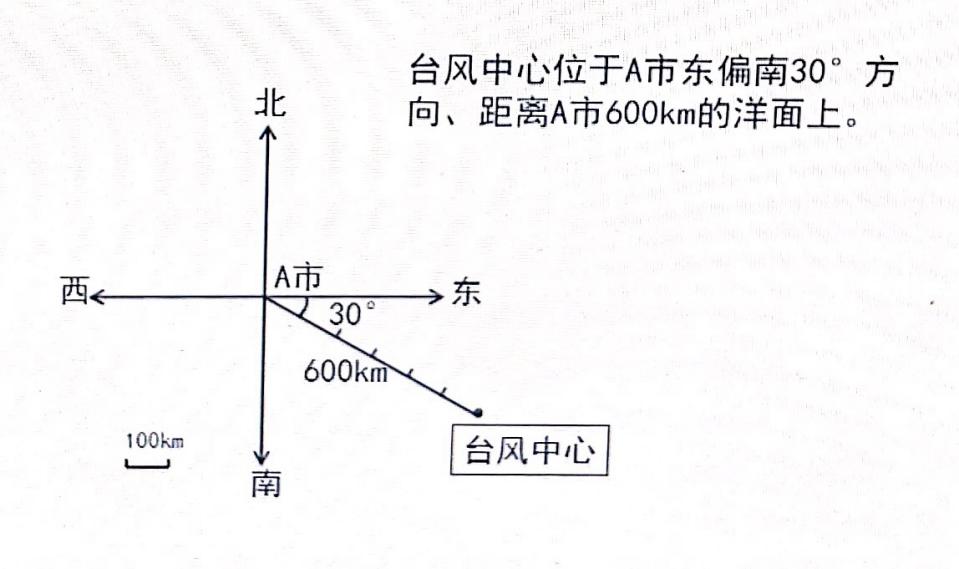
方位：

数形结合的例子在小学数学中无处不在，教师在教学中渗透数形结合的思想，使学生受到数学思想的启迪和熏陶是极其重要的。这样才能体现数学教学的 本质。

2 在活动中体验、感悟“数形结合”思想

数学思想往往是说不明，道不清的，要靠学生在丰富多彩的数学活动中自己去观察、思考、体会和感悟。如教学1+3=2² 1+3+5=3² 1+3+5+7=4² …………让学生自主探索规律，学生会先计算出结果，分别等于2、3、4的平方数，再根据结果寻找出规律：从1开始的连续奇数相加的和等于奇数个数的平方。你能解释这个规律吗？用什么方法解释这个规律？这时老师会组织学生思考讨论，得知借助图形来解释规律。

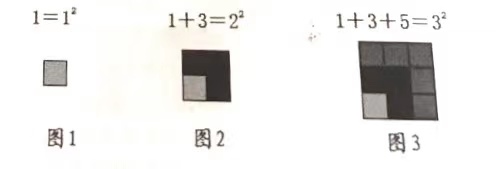
学生借助小正方形边操作演示，边汇报解释,如图2，由“1”想到1个小正方形，1个小正方形至少增加3个小正方形（1+3），才能拼成一个更大的正方形，而这个正方形的每行每列都是2个小正方形，即共有2²个小正方形，因此1+3=2² 。以此类推，4个小正方形至少增加5个小正方形才能得到一个较大的正方形，而这个正方形的每行每列都是3个小正方形，即共有3²个小正方形，故1+2+5=3^2. 。学生通过数学活动摆小正方形，借助图形直观形象的特点来理解数的规律。又如教学1/2+1/4+1/8+1/16+1/32+1/64+.....=。乍看到题目时，学生无从下手。让学生动手画图

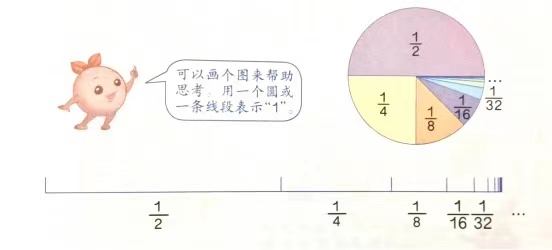
利用分数的直观模型或线段图，使学生一目了然发现结果等于1。数形结合让学生直观理解了“无限”的抽象概念。极其抽象的极限问题，因为经过学生动手画图形，就变得十分直观和便捷了。在教学中，教师往往设计让学生画一画、摆一摆、连一连等形式各样的数学活动，学生在参与数学活动中感悟到了数与形的完美结合，体验到了数学思想的价值与魅力，丰富了活动经验，提高了自主探究与合作学习能力，同时培养了学生的数学核心素养。

3 利用“数形结合”探索通用模式解决问题

数形结合的方法可以使抽象的数学问题直观化、生动化，有助于把握数学的本质，让很多问题迎刃而解，快捷简便，达到以简驭繁的目的。如教学下面一题

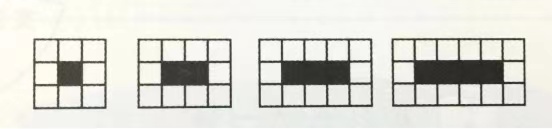
照着样子接着画下去，第六个图形分别有多少个黑色和白色小正方形。第十个图形呢？

仔细观察，本题图形位置和数量间的关系可以利用数形结合思想来解答。是第几个图形就有几个黑色小正方形，白色小正方形的个数是黑色小正方形的2倍多6个，从而发现解题的通用公式是2n+6。为学生解决问题建立了模型。再利用这个通用公式解决更多的问题。

数形结合的运用，“以形助数，以数解形，数形结合”，无论哪种形式的呈现，都体现着数形结合的思想。著名数学家华罗庚先生曾说，数缺形时少直观，形少数时难入微，数形结合百般好，隔家分离万事休。恰当合理地使用数形结合的方法，能使学生在解决数学问题时起到事半功倍的作用。并提高了学生的思维能力。培养学生的数学思想是学习数学的本质，是学生获得终生发展必需的数学素养的方法。

参考文献 ：

[1]佚名. 核心素养下小学数学数形结合思想的渗透与应用[J]. 新课程导学, 2019(3).

[2]单媛媛.浅谈“数形结合”在小学第一学段“数概念”教学中的运用策略［J］.科教文汇 （下旬刊） 2014（04） ：156－157．

[3]小学数学六年级上册“教师用书”