佛山市高明区第一中学 广东 佛山 528500
2021年佛山一模第18题是一道传统的解三角形题,在梯形中求解面积和角度问题,既考查了梯形的有关性质,又考查解三角形的知识,全面考查了学生分析问题、知识迁移、运算求解、解决问题的能力,本文主要是对第(2)问的解法进行探究,引导学生横向探究,促进学生思维的发展,挖掘数学知识的本质、渗透数学思想、提升数学素养。
一、问题提出
如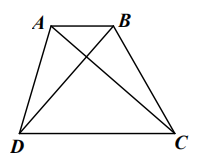 图,在梯形
图,在梯形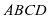 中,
中, ,
,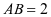 ,
,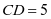 ,
,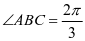 .
.
(1)若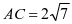 ,求梯形
,求梯形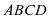 的面积.
的面积.
(2)若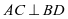 ,求
,求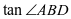 .
.
通过评卷发现,对于第(1)问大多数学生能够解决,对于第(2)问,学生困难很大,能够解出来的很少,得分率偏低。这引起了我的思考,我们的数学复习应该怎样更有效,学生的解题能力、解决问题能力的薄弱点在哪里。很明显,大多数学生对解三角形的知识只是停留在记忆正弦定理、余弦定理的层次,直接套用公式的题能够解决,对于多边形问题、陌生的图形、不太常规的题型就显得束手无策。让学生摆脱思维定势的束缚,善于独立思考,具有良好的知识迁移能力,探索解题新方法,积极主动解决问题是高考数学复习关键所在。
由于第(1)问难度较低,学生基本上能做对,方法也计较相似,所以本文就第二问的解法进行探究。
解法一 设 ,
,
则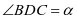 ,
,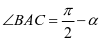 ,
,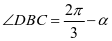 ,
,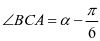 ;
;
在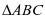 中,由正弦定理得
中,由正弦定理得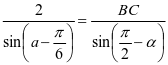 ;
;
在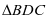 中,由余弦定理得
中,由余弦定理得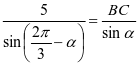 ;
;
两式相除得 ,展开得
,展开得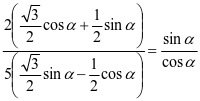
所以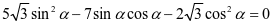 ,即
,即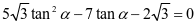
解得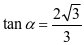 或
或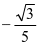 ,因为
,因为 ,则
,则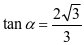 ,即
,即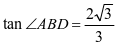 .
.
评析 这是参考答案上使用的方法,这种解法比较自然,设一个角作为变量,利用角度之间的关系进行转化、在三角形中运用正弦定理、最后求解一元二次方程即可得到答案。此方法对学生的化简计算能力要求比较高,并且要对三角恒等变化比较熟练才能迅速解题。
解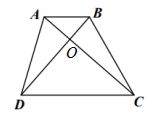 法二 设
法二 设 ,
,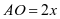 ,因为
,因为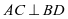 交于点
交于点 ,则
,则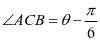 ,
,
因为 ,所以
,所以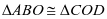 ,
,
则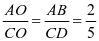 ,
,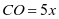 ,
, ;
;
在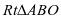 中,
中,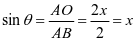 ,所以
,所以 ;
;
在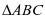 中,由正弦定理得
中,由正弦定理得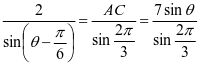 ;
;
展开得 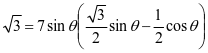 即
即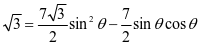
化简得 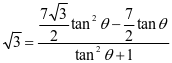 ,整理得
,整理得 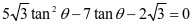 ;
;
解得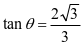 或
或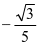 ,因为
,因为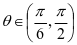 ,则
,则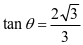 ,即
,即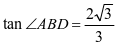 .
.
评析 此方法充分考虑了三角形的边与边的比例关系,利用相似比构造边与角的关系,再利用正弦定理解三角形,此方法与解法一比较类似,也是对解三角形一般方法的巩固,利用方程的思想解题,计算量还是比较大,但更具思维性。
解 法三 设
法三 设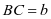 ,
,
在梯形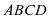 中,有
中,有
所以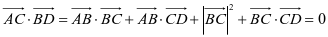
则  ,
,
整理化简得 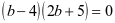 , 解得
, 解得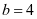 ,即
,即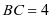 ;
;
在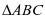 中,由余弦定理得
中,由余弦定理得 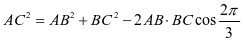 ,
,
解得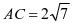 ; 因为
; 因为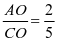 , 所以
, 所以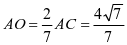 ;
;
在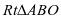 中,易得
中,易得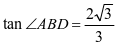 .
.
评析 此方法充分挖掘题目所给的已知条件,结合平面向量数量积运算的特点,直接利用向量的计算出 的长度,再利用解三角形的常用方法能够轻松的解决问题。此法计算量明显减少,不再单纯地局限正弦定理、余弦定理解三角形,与平面向量知识联系起来,体现了知识间的交汇。实际上,教材上余弦定理就是通过向量的方法来证明的,这种解法能开阔学生的思维,有助于学生弄清知识的来龙去脉,提升数学素养。
的长度,再利用解三角形的常用方法能够轻松的解决问题。此法计算量明显减少,不再单纯地局限正弦定理、余弦定理解三角形,与平面向量知识联系起来,体现了知识间的交汇。实际上,教材上余弦定理就是通过向量的方法来证明的,这种解法能开阔学生的思维,有助于学生弄清知识的来龙去脉,提升数学素养。
解法四 如右图:设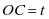 ,
,
由题意可知 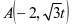 ,
,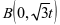 ,
,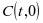 ,
,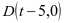 ;
;
因为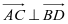 ;
;
所以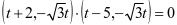 ;
;
即 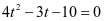 ,解得
,解得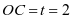 ;
;
所以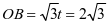 ,
,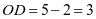 ;
;
所以有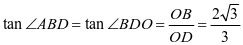 .
.
评析 此方法完全摆脱解三角形的惯用方法,把一个平面几何问题坐标化,利用平面直角坐标系和向量的坐标运算解题,大大减少了运算量。思路上突破定势思维,与解析几何联系起来,对于高三学生来说,必须具备该种能力,把一些复杂的几何问题坐标化,加强知识间的联系,体会坐标法解题的优势,提升解决问题的能力。
解 法五 如右图:设
法五 如右图:设 ,
,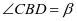 ;
;
因为 ,即
,即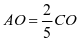 ,
,
所以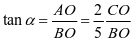 ,
,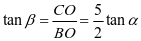 ,
,
又因为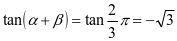 ,
,
所以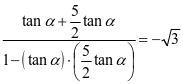 ,解得
,解得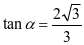 .
.
评析 此方法学生容易忽视,既没有用到正弦定理和余弦定理,也没有利用平面向量,而是利用边长的关系,再运用两角和的正切公式直接求解,计算量比较小,是解决此题较好的方法。此方法思维能力要求不是很高,但对于学生而言,怎样把恒等变换的公式与解三角形的实际问题结合起来是一个难点,要求学生具有较强的知识迁移能力,复习时应该加强这方面的训练,从而提升能力。
追根溯源,回归教材,探索新知,不仅可以让学生重温教材中的知识概念、公式定理,还能让学生深入理解数学思想方法。引导学生横向联系、探究不同解法,可以让学生跳出思维的定势和知识的禁锢,加强数学知识方法的联系,促进学生思维的发展,做到一题多解、多题一解,达到融会贯通的境界,提升学习能力和学科素养。
2