钢筋混凝土梁抗剪承载能力计算理论浅析

伯金山

重庆交通大学

摘要：钢筋混凝土梁的剪切破坏具有重要性与复杂性，很多学者对此问题从各方面进行了研究。根据国内外已有的钢筋混凝土梁抗剪性能研究成果，本文总结了各种抗剪承载力的计算基本原理与方法，对比了不同行业规范斜截面抗剪承载力计算公式异同，展望了未来抗剪承载能力计算需要努力的方向。

关键词：钢筋混凝土梁 抗剪承载力 计算理论

0引言

近百年来许多研究者提出了众多剪切破坏分析方法，主要有极限平衡理论、塑性理论、统计分析法等，同时根据不同的规范，有着不同的抗剪计算公式。

1.1塑性理论

塑性理论作为材料研究的一个分支，被用来解决钢筋混凝土结构在复杂受力状态下的强度问题。塑性理论的基本假定如下：

(1) 材料的应力-应变关系。假定钢筋是刚塑性材料，且不承受剪应力。因受压钢筋受力较小而略去不计，混凝土也视作为刚塑性材料。

(2) 材料的屈服条件。假定钢筋仅承受拉力，处于单向受拉状态，故屈服强度与普通钢筋材料相同。假定混凝土为抗拉强度为零的修正摩尔-库仑材料，破坏包络线只存在于受压区并满足其破坏准则。

(3) 塑性铰线。在塑性理论的上限解中，假定结构破坏时形成一个机动体系，该体系由若干个刚性区组合而成。各个刚性区之间由塑性铰或塑性铰线相连，然后建立塑性功方程。因刚性区内部不做功，故塑性内功全部集中在塑性铰或塑性铰线上。

(4) 混凝土的有效抗压强度。通过引入折减系数，将混凝土假定为有“屈服台阶”的刚塑性材料。

在上述假定条件下，可以求得钢筋混凝土梁在集中荷载或均布荷载作用下抗剪强度的上、下限解， 同时也是精确解。

1.2极限平衡理论

极限平衡理论主要研究了钢筋混凝土构件剪切坏机理，并通过极限破坏状态下的平衡求解抗剪承载力。就其本质而言，主要是采用试验统计公式，给公式中的每一项赋予物理概念和解释。

斜截面极限平衡理论有如下特点：

1) 联立求解斜截面上内力平衡方程组，而不是孤立地求解平衡方程；

2) 计算过程中不仅考虑箍筋内力， 还考虑混凝土的咬合力及纵向受拉钢筋的轴力和剪应力；

3) 混凝土的压力和剪力不是按照经验公式确定的，而是按照斜裂缝形成和发展过程中，由正应力和剪应力的分布图形及平面应力状态下混凝土的强度准则确定的。

虽然极限平衡理论可以获得相当高的计算精度，但这种理论需建立多个联立方程，计算过程比较复杂，应用不方便。

1.3统计分析法

由于抗剪机理的复杂性，想要准确预测构件的抗剪承载力比较困难，目前尚未获得比较统一的理论计算公式，而统计分析法一般是基于大量试验数据的回归分析，给出形式比较简单的计算公式，更易于应用。

故许多研究者借助于大量试验结果的数理统计分析，结合理论模式，在规范中建立一些关于有腹筋钢筋混凝土梁抗剪承载力计算公式，这些公式大多是以试验结果偏下限作为依据。这种模型建立的基本出发点并非要准确预测构件的抗剪承载力，而是防止构件的剪切破坏。

统计公式形式简单、有效、实用，因而应用广泛，但也存在试验工作量大、公式使用范围窄等缺点。

2不同设计规范中抗剪承载力计算公式

2.1《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG3362-2018）

对矩形、T形和I形截面等高度钢筋混凝土简支梁( 包括悬臂梁) 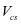按下式计算：

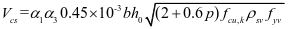
弯起钢筋的抗剪承载力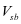 为：

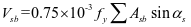
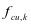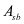式中： 为混凝土强度等级； 分别为弯起钢筋和箍筋抗拉强度设计值； 为与斜裂缝相交的配置在同一弯起平面内的弯起钢筋截面面积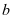； 为矩形截面的宽度， T 形或 I 形截面的腹板宽度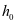； 为构件截面的有效高度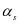； 为弯起钢筋与梁轴线的夹角；为斜截面内纵向受拉钢筋配筋百分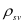率； 为配箍率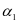； 为异号弯矩影响系数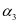； 为受压翼缘影响系数。

2.2《美国混凝土规范》（ACI318-08）

该规范的受剪承载力设计公式为

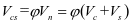
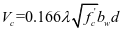
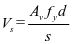
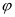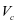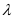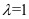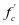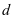为受剪承载力折减系数。取0.75； 为腹筋构件承载力， 为考虑轻骨料对混凝土强度折减系数，对于普通混凝土，取 ； 为圆柱体抗压强度； 为腹板宽度或圆形截面直径； 为从受压边缘纤维至纵向受拉钢筋重心得距离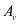； 为间距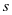 内抗剪钢筋的面积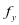； 为规定的非预应力钢筋的屈服强度。且要满足

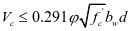
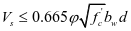
当总设计剪力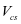 超过混凝土承担的剪力 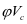一半的截面预应力和非预应力混凝土受弯构件，要按钢筋的最小面来配置钢筋，抗剪钢筋面积不小于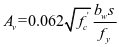

2.3欧洲规范（EN 1992-1-1）

有腹筋构件受剪承载力

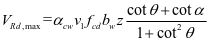
取上述公式中的较小值。

式中， 为混凝土压碎时的剪力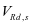； 为箍筋屈服时的剪力； 为箍筋截面面积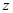； 为对于高度不变的构件所考虑单元最大弯矩的内力臂，近似取 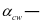； ； 对于钢筋混凝土结构，取1．0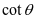； 建议值为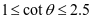 。公式需满足：

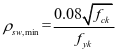
式中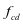： 为混凝土屈服强度设计值；

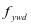为箍筋屈服强度设计值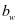； 为拉杆和压杆的最小宽度、高度修正系数，且 。

在任何情 况 下 不 应 超 过 与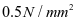 二者的较小值。 时，对梁配置最少箍筋

3结语

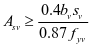
钢筋混凝土梁在剪力和弯矩共同作用的区段，可能发生沿斜截面剪切破坏，这种破坏的突发性会引发巨大灾难。近百年来，国内外学者一直努力通过各种理论及方法对剪切破坏机理进行诠释，提出了多种可行的抗剪承载力计算方法，并取得了显著的成效。虽然抗剪理论日渐成熟．但受到材料性能及结构形式的限制，抗剪承载力计算公式仍无法达成统一，故需将相关理论有机融合，进一步完善规范公式。

参考文献

1.公路钢筋混凝土及预应力混凝土桥涵设计规范 ( JTG3362-2018)．人民交通出版社，2018．

2.混凝土结构设计规范(GB50010-2010)[S]．北京：中国建筑工业出版社，2010．

3.钟小平．不同设计规范钢筋混凝土梁的抗剪承载力分析．特种结构．2009

4.刘彬，张建仁，王磊，羊日华．钢筋混凝土梁抗剪承载力计算理论述．中外公路．2011

5.ACI 318-08．Building Code Requirements for structure Concrete and Commentary [S]．AmericanConcrete Institute，2008．

作者简介：伯金山（1995-08-28），男，汉族，籍贯：重庆市忠县，当前职务：学生，学历：硕士研究生，研究方向：桥梁监控与检测

伯金山13114011302重庆市渝北区龙塔街道庆业九寨印象3栋（1本）