清远市源潭中学 广东省 清远市 511500
一、教学目标及核心素养
知识与技能:建立一次函数模型来刻画实际问题中变量间的关系;通过分析数量关系,尝试初步预测变量的变化规律,培养学生数据分析、直观想象的核心素养.
过程与方法:通过对实际问题中变量的一系列数据,在直角坐标系中观察点和这些点形成的图形,建立恰当的函数模型,求解函数模型,再利用求解的函数模型初步预测变量的变化规律,掌握相关知识和技能,培养分析、解决问题的能力.落实数学运算、逻辑推理及数学建模的核心素养.
情感、态度、价值观:体验一次函数的实际应用价值,积极利用所学知识解决实际问题,激发学习兴趣.
二、教学重、难点
重点:建立一次函数模型来刻画实际问题中变量间的关系.通过分析函数关系,尝试初步预测变量的变化规律.
难点:建立函数模型.
三、教学过程
(一)创设情境:
例1 同学们都有用过文具盒,我们市高新区新建了一家文具盒生产工厂,该工厂现在在试运营期,这段时间工作人员将日生产文具盒的总成本(元)与日产量(套)之间的关系统计如下表
日产量 | 1000 | 2000 | 3000 | 4000 | 5000 |
日总成本 | 36000 | 42000 | 48000 | 54000 | 60000 |
(1)请据此表能否估计出该厂每日的原始成本
(2)若日产量达到6500套,则该天总成本是多少?
(3)当前文具盒的出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒多少套?
(4)在(2)条件下,该厂亏盈情况如何?
设计意图:用学生熟悉的文具盒,从本市新建的文具盒工厂试运营期统计得到的数据入手创设情境,激发学生学习兴趣.
组织探究
教师:请以日产量为横坐标,该工厂日生产文具盒的总成本为纵坐标,画它们之间关系的的图象.
学生画完图后,教师用Excel软件生成散点图.
设计意图:例1没有给出明确的函数模型,数据表格也是函数的一种表示方式,借助计算机Excel软件生产散点图,体现数学与计算机技术融合.当然,学生动手作图也可取.毕竟受教学条件限制,不可能人手一台电脑,只能教师演示.
新课讲解
由Excel做出的散点图的分布特征判断,该工厂日总产量y与日产量x之间的函数关系近似为一次函数  .(关于函数模型的选取,用西沃白板5制作课件时设置游戏环节,便于学生选取跟本题相关的函数模型及该函数相关知识,即复习了知识又增加了趣味性.)
.(关于函数模型的选取,用西沃白板5制作课件时设置游戏环节,便于学生选取跟本题相关的函数模型及该函数相关知识,即复习了知识又增加了趣味性.)
取函数图象上两点的坐标:(1000,36000)、(2000,42000)代入函数解析式,得方程组
 解得
解得
所以
将 代入上式得
代入上式得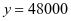 ,与真实数据一致.
,与真实数据一致.
因此 是符合实际的函数模型.
是符合实际的函数模型.
(建模、解模及验证模型,在西沃课件中使用蒙层、拖拽等功能,帮助学生逻辑严谨的规范书写解题过程)
该厂每日的原始成本即产量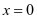 时
时 的值,为30000元
的值,为30000元
当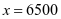 时,
时,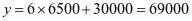 元
元
设利润为z,因利润z=12x-(6x+30 000), 所以z=6x-30 000,由z≥0解得x≥5 000,
故至少日生产文具盒5 000套.
由(3)可知日产量达到6500套时,该厂是盈利的,此时利润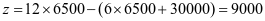 元
元
(将数学问题运算的结果转化为实际问题的结论,为使学生形成书写规范的好习惯,制作课件时用了“留白”、拖拽等功能)
方法归纳
(1)在实际应用中,建立合适的函数模型,把实际应用问题转化为数学问题为关键点.
解答函数实际应用问题时,一般要分哪四步进行?
第一步:分析、联想、转化、抽象;
第二步:建立函数模型,把实际应用问题转化为数学问题;
第三步:解答数学问题,求得结果;
第四步:把数学结果转译成具体问题的结论,做出解答.
而这四步中,最为关键的是把第二步处理好.只要把函数模型建立妥当,所有的问题即可在此基础上迎刃而解.
(2)一次函数模型的应用
利用一次函数求最值,常转化为求解不等式ax+b≥0(或≤0).解答时,注意系数a的正负,也可以结合函数图象或其单调性来求最值.
设计意图:方法归纳如同“画龙点睛”,作为高中阶段数学建模的第一课,将建模步骤详细归纳很有必要.
当堂练习
商店出售茶壶和茶杯,茶壶定价为每个20元,茶杯每个5元,该商店推出两种优惠办法:
①买一个茶壶赠一个茶杯;
②按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯x(个),付款y(元),试分别建立两种优惠办法中y与x之间的函数解析式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠?
设计意图:此问题情境与实际生活息息相关,学生做题兴趣很浓厚,同时也能巩固所学.课堂上,小组合作完成.
解:由优惠办法①可得函数解析式为y1=20×4+5(x-4)=5x+60(x≥4,且x∈N).
由优惠办法②可得y2=(5x+20×4)×92%=4.6x+73.6(x≥4,且x∈N).
y1-y2=0.4x-13.6(x≥4,且x∈N), 令y1-y2=0,得x=34.
所以,当购买34个茶杯时,两种优惠办法付款相同;
当4≤x<34时,y12,即优惠办法①更省钱; 当x>34时,y1>y2,优惠办法②更省钱.
反思
《普通高中数学课程标准(2017年版2021年修订)》明确指出:“数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养”,“在现实问题中,能够利用函数构建模型,解决问题”.本节课是一节相对简单的函数建模课,目的是让初入高中的学生明确数学建模的流程和步骤,建模能力的形成是一个循序渐进、潜移默化的过程,有待于在后续教学与学习中继续加强.

3