上好函数概念课，敲开函数入门砖

上好函数概念课，敲开函数入门砖

卢梦宁，覃又马

河池市金城江区第二初级中学广西河池 547000

【摘要】准确把握函数概念的内涵和外延，通过正反实例让学生进行分析、比较、鉴别帮助学生深刻理解函数概念，将抽象的函数概念具体化

【关键词】函数；变量；单值对应

概念教学是初中数学教学的重点，也是难点，要重视基本概念的教学。而函数是初中阶段最重要的概念之一，因此就更加有必要重视函数概念教学的研究。

1函数在数学中的重要地位

恩格斯说：“数学的转折点，是笛卡尔的变数。有了变数，运动进入了数学；有了变数，辩证法进入了数学。”函数促进了数学的进一步研究与发展。

函数是研究数量关系的重要工具，人们借助函数构建模型，刻画现实生活中的数量关系，并通过对数量关系的研究来解决现实生活中的问题。

函数与方程、不等式有密切的联系，而函数起到统领的作用，是代数学的核心内容，同时函数还是沟通代数、几何内容的桥梁。

函数内容蕴涵着重要的数学思想方法，如函数思想，方程思想，分类讨论思想，数形结合思想，待定系数法、配方法等。这些思想方法是进一步学习数学和解决数学问题的基础。

因此函数成为初中阶段最重要的概念之一，非常有必要对函数概念的教学进行研究。

2学习函数概念的难点

函数产生于研究变量之间关系的需要，而学生对于用“变量”这种运动、变化的观点来看待问题的能力比较弱、概念形成的水平低，因此学生学习函数概念的难点在认知水平上的困难。

由于函数概念的表述比较抽象，含义深刻，学生不能从其定义的文字上真正理解它的内涵，把握不准函数的本质。

3.函数概念教学浅析

3.1实例引入，化抽象为具体

基于学生的认知水平和学习函数的难点，函数概念的引入应遵循从特殊到一般，从具体到抽象，由浅入深，由易到难的认识规律，举一些学生熟悉的特殊例子，通过对具体实例的分析，抽象出函数的本质属性，然后归纳出函数概念。

其实，在学生已有经验中，有许多可以用以说明函数产生过程的实例。基于这一认识水平，进行函数概念教学时，从实例引入，让学生经历从具体到抽象，参与函数概念的形成过程。

例如：我们可以通过研究多边形的内角和与边数之间的关系归纳出函数概念。

下表是描述多边形的边数（x）与内角和（y）之间的关系：

引导学生观察表格思考以下问题：

①在这个变化过程中，有哪几个变量？

②对于变量x的每一个确定的值，变量y有几个值与它对应。

通过对以上两个问题的解决，归纳出函数概念：在一个变化过程中，如果有两个变量x与y，对于变量x的每一个确定的值，变量y都有唯一确定的值与它对应，我们说x是自变量，y是x的函数。

这是从以上具体的实例抽象概括后的描述，其中居于主动地位的多边形的边数x是自变量，随之而变化且有唯一对应值的内角和y叫做自变量x的函数。

3.2抓关键词，剖析概念内涵

抓住概念中的关键词“两个变量”“唯一确定”，通过对关键词的分析，得出函数概念包含的两个条件：①两个变量；②单值对应。这也是判断两个变量是否具有函数关系的依据。

但是函数这一抽象的概念，我们不要期望一节课或者几节课就能让学生很好地理解，特别是对“单值对应”这一关系的理解，还需要通过各种具体的例子加以解释与分析，帮助学生加深对函数概念理解。

3.3正反举例，多角度辨析概念

心理学研究发现：学生对概念外延的掌握优于对概念内涵的掌握，准确把握函数概念的内涵和外延，尽量将抽象的函数概念具体化，通过正反实例让学生进行分析、比较、鉴别帮助学生深刻理解函数概念，从而达成教学目标。

我们知道描述两个变量之间关系的方法常用的有三种：图象法、列表法、解析法，每种表示都可独立抽象出函数概念。能否正确地在各种表示之间进行灵活转换是考查函数概念形成水平的一个重要标准。因此我们可从三个不同的角度来分析函数的单值对应关系。

3.3.1从解析法这个角度举例分析,帮助学生理解函数概念

正例1：已知，一个乒乓球的售价是0.5元/个，若购买乒乓球的数量为x个，需要支付的费用为y元，那么y与x的关系为：y=0.5x．

紧扣函数概念对这一变化过程进行两个追问：

①这个问题研究哪两个变量之间的关系？

②当x=1时，y=；当x=2时，y=。对于变量x取一个确定的值时，另一个变量y有没有唯一值与它对应？

通过对以上两个问题的解答，让学生明确两个问题①这个问题是研究两个变量

y与变量x之间的关系；②对于变量x的每一个确定的值，变量y都有唯一确定的值与它对应，是单值对应关系，满足函数概念。从而得出当x是自变量，y是自变量x的函数。

为了让学生准确理解函数概念中的单值对应关系，还应该补充反例进行对比分析。

反例2：在a²=s中，当s=1时，a=1或—1，也就是说当s取一个值时a有两个值与它对应，不满足函数概念中的单值对应关系，所以a不是s的函数。

反例3：在︱m︱=n+1中，m是n的函数吗？为什么？

通过正反实例让学生辨析单值对应与非单值对应的区别，从而更加透彻的理解函数概念的内涵。

3.3.2从列表法这个角度举例分析,帮助学生理解函数概念

正例：如表一：

s	1	2	3	…
m	3	6	9	…

思考：这个表格描述的哪两个变量之间的关系？当s取1时，m有哪个值与之对应？是有唯一值与之对应吗？如果把s看作自变量，那么m是s的函数吗？

反例：如表二：

x	3		5		…
y	3	-3	5	-5	…

思考：这个表格描述的哪两个变量之间的关系？y是x的函数吗？为什么？

3.3.3从图象法这个角度举例分析，帮助学生理解函数概念

例：如图，下列表示y是x的函数的是

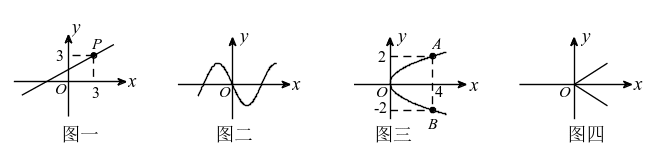
结合图形思考以下问题：

①在上列各图中，当横坐标x发生变化时，对应的点是否变化？对应点的纵坐标y是否跟着发生变化？图形中点的横坐标x和纵坐标y是变量吗？

②如图一，当x=3时，对应图象上点P的纵坐标y=，对于变量x的每一个确定的值，变量y是否有唯一确定的值与它对应？那么y是x的函数吗？图二呢？

③如图三，当x=4时，对应图象上点有几个？此时y=，对于变量x的每一个确定的值，变量y是否有唯一确定的值与它对应？那么y是x的函数吗？图四呢？

以上几个问题的设计是紧扣函数概念，从学生的认知水平出发，循序而问，由表及里，层层深入，在认知上克服重重障碍，引导学生理解量与量的相依关系，在对比中理解单值对应关系，让学生对函数概念的理解得到进一步的认识与强化。通过这一概念的形成引发学生思维水平的一个飞跃，感悟用三种方法表示函数，可以从不同的角度观察函数的变化规律，为今后学习函数的性质作一个伏笔。

总之，函数概念是初中阶段最重要的概念之一，抽象难以理解，但是只要抓住概念的内涵，通过各种具体的例子加以解释与分析，就能揭开函数神秘的面纱，敲开函数之大门，为进一步学习函数做好充分的准备。

参考文献

[1]孙一文.初中数学函数模块的教学策略[J].科技资讯,2020,18(34):103-104+107.

[2]章建跃.如何帮助学生建立完整的函数概念[J].数学通报,2020,59(09):1-8.